python代码实现多项式回归

核心思路：将非线性数据通过参数替换的方法转换到线性数据，然后再使用线性回归的方法进行拟合。

对于函数y=ax平方+bx+c为例：

方法1：手写代码实现

（1）导包

# 第一部分：导包
from sklearn.linear_model import LinearRegression
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

（2）获取数据集

# 第二部分：获取数据集并绘制散点图
x = np.random.uniform(-4, 2, size=(100))
y = 2 * x**2 + 4 * x + 3 + np.random.randn(100)
x = x.reshape(-1, 1)  # 确保 x 是二维数组
# 绘制散点图
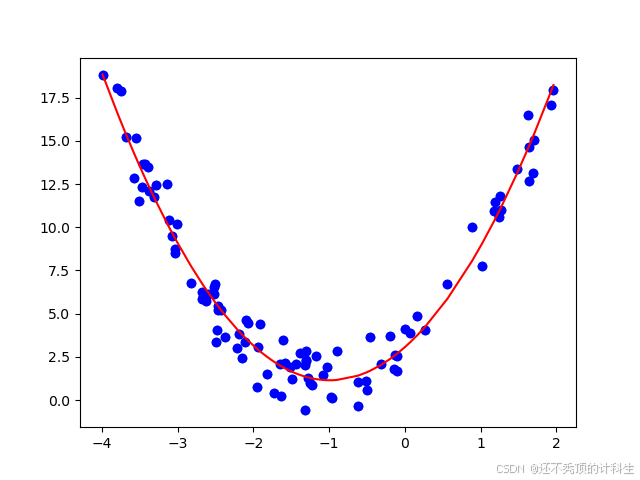
plt.scatter(x, y)

（3）多项式回归

# 第三部分：多项式回归
X_new = np.hstack((x, x**2))  # 合并 x 和 x^2 成为矩阵
linear_regression_new = LinearRegression()  # 线性回归模型
linear_regression_new.fit(X_new, y)  # 训练模型,训练的时候内部用的就是有两个特征值的非线性公式

（4）预测结果

# 第四部分：预测结果
y_predict_new = linear_regression_new.predict(X_new)
# 绘制预测结果的回归曲线
plt.scatter(x, y,color='blue')
plt.plot(np.sort(x, axis=0), y_predict_new[np.argsort(x, axis=0)], color='red')  # 排序绘制曲线
'''
x 的形状是 (n, 1)，表示 x 是一个二维数组（n 行 1 列）。
axis=0 表示沿着第 0 轴，也就是沿着行的方向排序。
因为 x 是一列数据，axis=0 确保对每一列（在这里就是 x 的唯一一列）中的值按行排序，这样可以将 x 从小到大排列。
'''
plt.show()

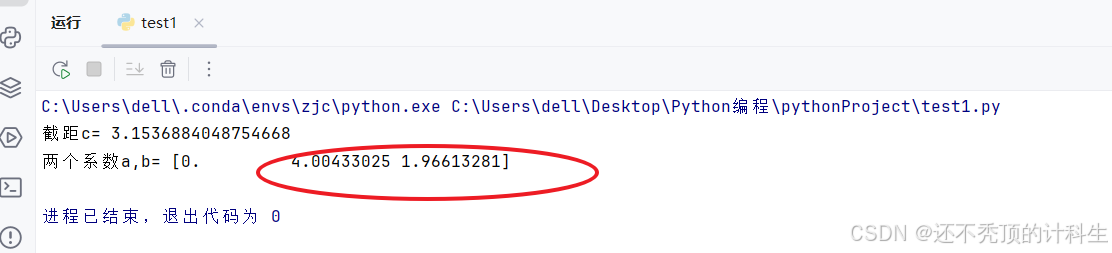
print("截距c=", linear_regression_new.intercept_)
print("两个系数a,b=",linear_regression_new.coef_ )

（5）pycharm代码完整实现

# 第一部分：导包
from sklearn.linear_model import LinearRegression
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# 第二部分：获取数据集并绘制散点图
x = np.random.uniform(-4, 2, size=(100))
y = 2 * x**2 + 4 * x + 3 + np.random.randn(100)
x = x.reshape(-1, 1)  # 确保 x 是二维数组
# 绘制散点图
plt.scatter(x, y)

# 第三部分：多项式回归
X_new = np.hstack((x, x**2))  # 合并 x 和 x^2 成为矩阵
linear_regression_new = LinearRegression()  # 线性回归模型
linear_regression_new.fit(X_new, y)  # 训练模型,训练的时候内部用的就是有两个特征值的非线性公式

# 第四部分：预测结果
y_predict_new = linear_regression_new.predict(X_new)
# 绘制预测结果的回归曲线
plt.scatter(x, y,color='blue')
plt.plot(np.sort(x, axis=0), y_predict_new[np.argsort(x, axis=0)], color='red')  # 排序绘制曲线
'''
x 的形状是 (n, 1)，表示 x 是一个二维数组（n 行 1 列）。
axis=0 表示沿着第 0 轴，也就是沿着行的方向排序。
因为 x 是一列数据，axis=0 确保对每一列（在这里就是 x 的唯一一列）中的值按行排序，这样可以将 x 从小到大排列。
'''
plt.show()

print("截距c=", linear_regression_new.intercept_)
print("两个系数a,b=",linear_regression_new.coef_ )

方法2：使用库函数实现

更改部分：“第三部分：多项式回归”，代码如下：

# 第三部分：多项式回归
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=2)#代表最高为二次幂
X_new = poly.fit_transform(x)#得到的第一列为序号，第二列为X，第三列为X的平方
linear_regression_new = LinearRegression()  # 线性回归模型
linear_regression_new.fit(X_new, y)  # 训练模型,训练的时候内部用的就是有两个特征值的非线性公式

完整代码如下：

# 第一部分：导包
from sklearn.linear_model import LinearRegression
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# 第二部分：获取数据集并绘制散点图
x = np.random.uniform(-4, 2, size=(100))
y = 2 * x**2 + 4 * x + 3 + np.random.randn(100)
x = x.reshape(-1, 1)  # 确保 x 是二维数组
# 绘制散点图
plt.scatter(x, y)

# 第三部分：多项式回归
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=2)#代表最高为二次幂
X_new = poly.fit_transform(x)#得到的第一列为序号，第二列为X，第三列为X的平方
linear_regression_new = LinearRegression()  # 线性回归模型
linear_regression_new.fit(X_new, y)  # 训练模型,训练的时候内部用的就是有两个特征值的非线性公式
# 第四部分：预测结果

y_predict_new = linear_regression_new.predict(X_new)
# 绘制预测结果的回归曲
plt.scatter(x, y,color='blue')
plt.plot(np.sort(x, axis=0), y_predict_new[np.argsort(x, axis=0)], color='red')  # 排序绘制曲线
'''
x 的形状是 (n, 1)，表示 x 是一个二维数组（n 行 1 列）。
axis=0 表示沿着第 0 轴，也就是沿着行的方向排序。
因为 x 是一列数据，axis=0 确保对每一列（在这里就是 x 的唯一一列）中的值按行排序，这样可以将 x 从小到大排列。
'''
plt.show()

print("截距c=", linear_regression_new.intercept_)
print("两个系数a,b=",linear_regression_new.coef_ )