多项式回归（Linear Regression）原理详解及Python代码示例

多项式回归原理详解

        多项式回归（Polynomial Regression）是线性回归（Linear Regression）的一种扩展形式。它通过在输入变量上添加高次项来拟合非线性关系。虽然多项式回归本质上还是线性模型，但它允许模型在输入特征的多项式基础上进行线性拟合，从而捕捉复杂的非线性关系。

1. 多项式回归的数学表达式

        假设我们有一个输入特征 x 和输出变量 y，多项式回归模型可以表示为：

                        y=β0+β1x+β2x2+β3x3+⋯+βnxn+ϵ

        其中，β0,β1,β2,…,βn是模型的参数，n 是多项式的阶数，ϵ是误差项。

2. 多项式回归的步骤

1. 选择多项式的阶数：选择合适的多项式阶数 n 是模型拟合的关键。阶数过低可能会导致欠拟合，阶数过高则可能导致过拟合。

2. 构建多项式特征：将输入特征扩展为多项式特征。例如，对于一个一维特征 x，构建的特征矩阵为

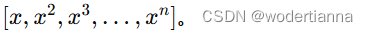
3. 拟合模型：使用线性回归方法在多项式特征上进行拟合。

4. 评估模型：通过均方误差（MSE）等指标评估模型的性能。

Python