生物统计学(biostatistics)笔记-5.EM&Motif finding

目录

EM算法

1、概念

2、关键步骤

3、EM计算实例

MCMC（Markov Chain Monte Carlo）：随机模拟

1、伪随机数生成

2、蒙特卡罗方法与MCMC

3、思想与方法

4、应用

Motif finding

1、生物知识

2、前置知识

3、模体识别问题与EM解决

4、算法MEME

---

EM算法

1、概念

最大期望算法（Expectation-maximization algorithm，又译为期望最大化算法），是在概率模型中寻找参数最大似然估计或者最大后验估计的算法，其中概率模型依赖于无法观测的隐性变量（Z）

2、关键步骤

第一步是计算期望（E），利用对隐藏变量的现有估计值，计算其最大似然估计值；

第二步是最大化（M），最大化在E步上求得的最大似然值来计算参数的值。M步上找到的参数估计值被用于下一个E步计算中，这个过程不断交替进行。

3、EM计算实例

• Step1:启始，随便给参数(硬币正面概率)
• Step2:E-step【状态估计】,计算得到期望，每一行结果然后求和
• Step3：M-step【最大化】使用期望改进参数
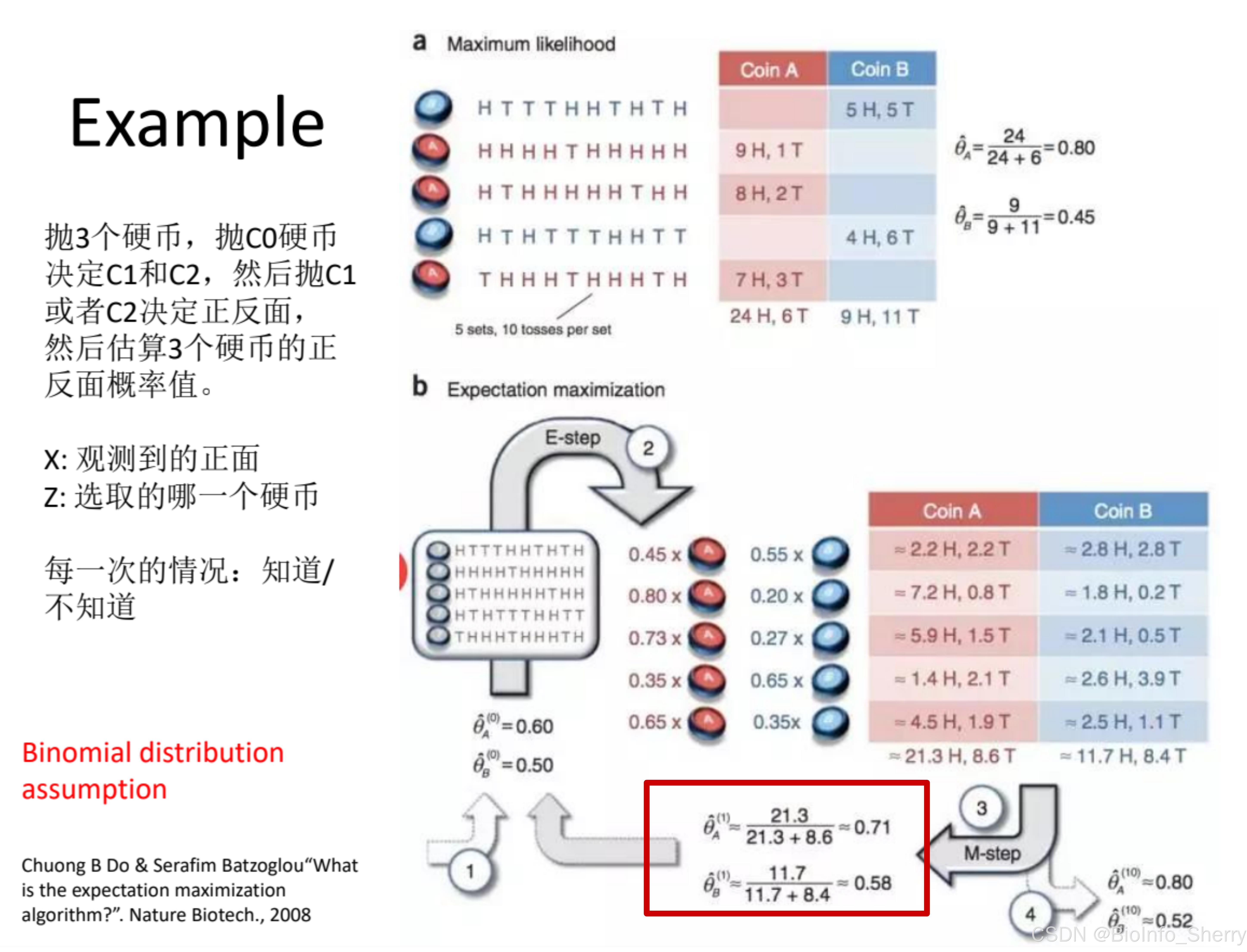
• Step4：结束，达到目标

MCMC（Markov Chain Monte Carlo）：随机模拟

1、伪随机数生成

• 计算机只能有伪随机数，遵循算法，特点：predictable and repeatable
• 算法：Linear congruence generator (LCG)，一般使用时间