本文介绍了寻找字符串中最长回文子串的不同方法，包括暴力法、动态规划（回文判断与位置判断）、滚动数组优化以及ManachersAlgorithm，展示了如何通过这些技术提高算法效率，降低时间复杂度和空间复杂度。
文章目录
题目
给你一个字符串 s，找到 s 中最长的回文子串。
如果字符串的反序与原始字符串相同，则该字符串称为回文字符串。
示例 1：
输入：s = “babad”
输出：“bab”
解释：“aba” 同样是符合题意的答案。
示例 2：
输入：s = “cbbd”
输出：“bb”
提示：
1 <= s.length <= 1000
s 仅由数字和英文字母组成
自己拿到手的做法：
1、直接两层for循环，开头字母固定，结尾字母遍历
分析：
1、暴力法：同上，列举所有可能，判断
2、动态规划：字符串反序，然后正反序对比
3、暴力破解优化
暴力法
可以，但是时间太长了，超时了
public String longestPalindrome(String s){
String ans = "";
int max = 0;
for(int i = 0; i < s.length(); i++){
for(int j = i + 1; j <= s.length(); j++){ //这里要 <= substring(i, j)不包括末尾坐标
String str = s.substring(i, j);
if(isHuiWen(str) && str.length() > max){
ans = s.substring(i, j);
max = Math.max(max, ans.length());
}
}
}
return ans;
}
private boolean isHuiWen(String s) {
for(int i = 0; i < s.length() / 2; i++){
if(s.charAt(i) != s.charAt(s.length() - 1 - i)){
return false;
}
}
return true;
}
动态规划
动态规划（回文判断，位置判断）
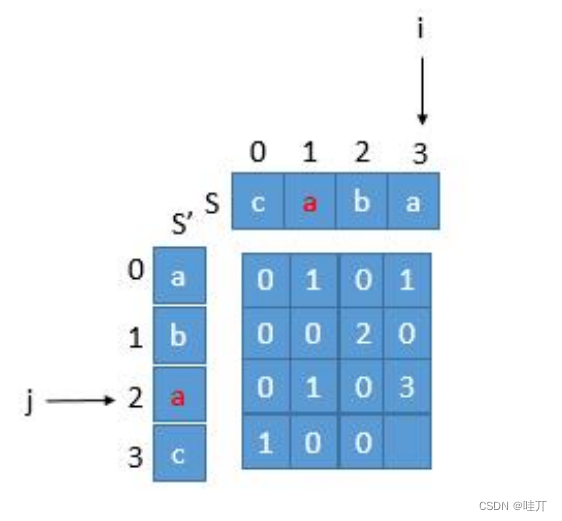
1、思想：字符串反序---->找出回文串
存在问题：回文串是可以找到的，但是找到的位置（反序和正序的相对位置）可能不是一个位置的，
所以导致可能匹配错误（S="abc435cba" ， s' = "abc534cba"为例）
解决方法：再找到回文串的时候，判断 反序的串转化过来是否和正序的位置一样
（不需要一个一个字母来判断，判断最后一个字母就可以了）
时间复杂度：两层循环O(n^2)
空间复杂度：一个二维数组O(n^2)
public class text2 {
public static void main(String[] args) {
}
public String longestPalindrome(String s){
if(s.equals("")){
return "";
}
String s2 = new StringBuffer(s).reverse().toString(); //字符串倒置
int len = s.length();
int[][] dp = new int[len][len];
int maxLen = 0;
int maxEnd = 0;
for(int i = 0; i < len; i++){
for(int j = 0; j < len; j++){
if(s.charAt(i) == s2.charAt(j)){
if(i == 0 || j == 0){
dp[i][j] = 1;
}else{
dp[i][j] = dp[i - 1][j - 1] + 1;
}
}
/*这里判断 ：在回文的前提下，是否在同一个位置上*/
if(dp[i][j] > maxLen){
int beforeRev = len - 1 - j; //倒置前的下标
if(beforeRev + dp[i][j] - 1 == i){ //下标是否对应
maxLen = dp[i][j];
maxEnd = i;
}
}
}
}
return s.substring(maxEnd - maxLen + 1, maxEnd + 1);
}
}
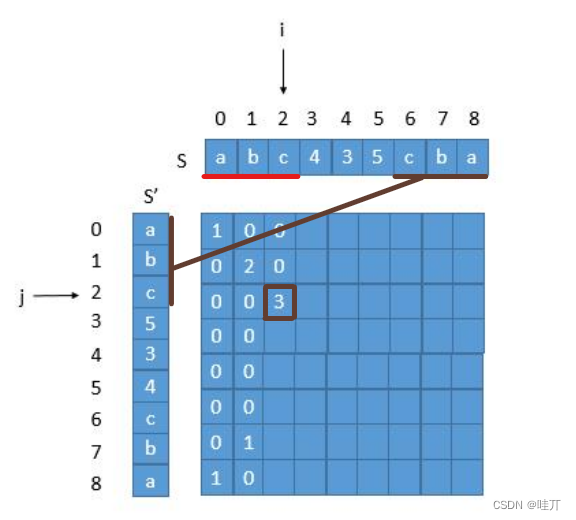
滚动数组（空间优化）
2、优化：滚动数组（一维数组）
从后往前
空间复杂度：O(n)
public class text2 {
public static void main(String[] args) {
text2 text2 = new text2();
text2.longestPalindrome("abc345cba");
}
public String longestPalindrome(String s){
if(s.equals("")){
return "";
}
String s2 = new StringBuffer(s).reverse().toString(); //字符串倒置
int len = s.length();
int[] dp = new int[len];
int maxLen = 0;
int maxEnd = 0;
for(int i = 0; i < len; i++){
/********************修改的地方**************************/
for(int j = len - 1; j >= 0; j--){
/********************修改**************************/
if(s.charAt(i) == s2.charAt(j)){
if(i == 0 || j == 0){
dp[j] = 1;
}else{
dp[j] = dp[j - 1] + 1;
}
/*****************修改的地方***********************/
}else{ //判断不相同的时候，数组置0
dp[j] = 0;
}
/********************************************/
if(dp[j] > maxLen){
int beforeRev = len - 1 - j; //倒置前的下标
if(beforeRev + dp[j] - 1 == i){ //下标是否对应
maxLen = dp[j];
maxEnd = i;
}
}
}
}
return s.substring(maxEnd - maxLen + 1, maxEnd + 1);
}
}
暴力破解优化
动态规划1
1、暴力法存在问题：时间太长（每次列举出来子串，每次都要判断回文）
优化：把子串的回文状况存起来（动态规划），在这个迭代过程中（少判断了好多次回文），判断长度
迭代公式：P(i,j)=(P(i+1,j−1)&&S[i]==S[j])
原理：先求len = 1 的，利用公式可知：能求出来 len = 3, 5 的
同理len = 2 的， 可以求出来 len = 4, 6的
在求3， 4， 5， 6....的时候1， 2的已经求出来了
时间复杂度：O(n^2)
空间复杂度：O(n^2)
优化：当我们求长度为 6 和 5 的子串的情况时，其实只用到了 4，3 长度的情况，而长度为 1 和 2 的子串情况其实已经不需要了。但是由于我们并不是用 P 数组的下标进行的循环，暂时没有想到优化的方法。
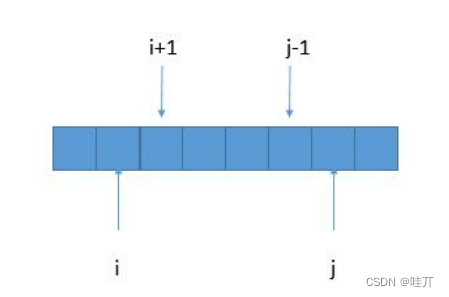
可以看出来这种方式是：按长度来遍历的，先是长度1， 后是长度2…
public String longestPalindrome(String s){
int length = s.length();
boolean[][] p = new boolean[length][length];
int maxLen = 0;
String maxPal = "";
for(int len = 1; len <= length; len++){ //遍历所有可能的长度
for(int start = 0; start < length - 1; start++){ //子串起始的位置
int end = start + len - 1; //算出子串结束的位置（依据起始和长度）
if(end > length) //下标越界，结束本次循环
break;
/*
* 判断回文（分分为前后两部分，&&前后，前：1 或 2 或 子串左右两边的是否回文 后：当前是否回文）
* 长度为1的时候start 和 end 是一样的
* 长度为2的时候，
* */
p[start][end] = (len == 1 || len == 2 || p[start + 1][end - 1]) && s.charAt(start) == s.charAt(end);
if(p[start][end] && len > maxLen){ //回文 && 长度大于当前max
maxPal = s.substring(start, end + 1);
}
}
}
return maxPal;
}
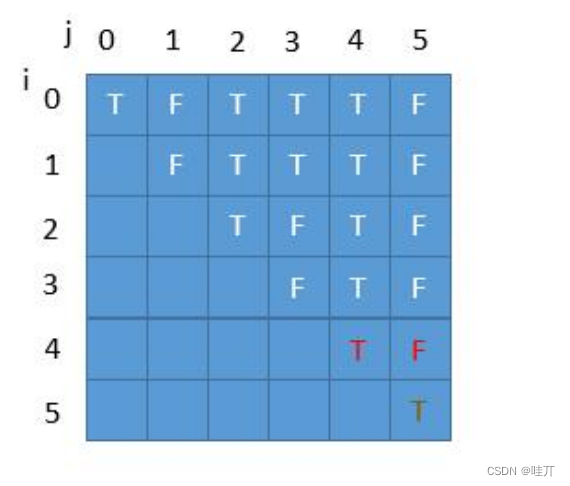
动态规划2
2、换一种动态规划的方式：（字符串）从后向前遍历
分析：这样看起来更合理，i 需要 i ＋ 1
迭代公式：P(i,j)=(P(i+1,j−1)&&S[i]==S[j])
但是：
时间复杂度：O(n^2)
空间复杂度：O(n^2)
这种是从底层向上递推的
public String longestPalindrome(String s) {
int n = s.length();
String res = "";
boolean[][] dp = new boolean[n][n];
//字符串 从后往前截取
for (int i = n - 1; i >= 0; i--) {
for (int j = i; j < n; j++) {
//j - i < 2 表示：长度是1的时候直接就true，是2及以上的话判断dp[i + 1][j - 1]（动态规划）
dp[i][j] = s.charAt(i) == s.charAt(j) && (j - i < 2 || dp[i + 1][j - 1]); //j - i 代表长度减去 1
if (dp[i][j] && j - i + 1 > res.length()) {
res = s.substring(i, j + 1);
}
}
}
return res;
}
滚动数组（空间优化）
3、优化：滚动数组（一维数组）
因为上面的是一层一层来递推的，下推上
public String longestPalindrome(String s) {
int n = s.length();
String res = "";
boolean[] P = new boolean[n];
for (int i = n - 1; i >= 0; i--) {
for (int j = n - 1; j >= i; j--) {
P[j] = s.charAt(i) == s.charAt(j) && (j - i < 3 || P[j - 1]);
if (P[j] && j - i + 1 > res.length()) {
res = s.substring(i, j + 1);
}
}
}
return res;
}
扩展中心
回文串一定是对称的，所以每次循环选择一个中心，进行左右扩展，判断左右字符串是否相等就行了
分析：
奇数串：从一个字符开始扩展 n个中心
偶数串：从字符中心开始扩展 n - 1 个中心
时间复杂度：O(n^2)
空间复杂度：O(1)
public String longestPalindrome(String s) {
if (s == null || s.length() < 1) return "";
int start = 0, end = 0;
for (int i = 0; i < s.length(); i++) { //要扩展的中心
int len1 = expandAroundCenter(s, i, i); //奇数
int len2 = expandAroundCenter(s, i, i + 1); //偶数
int len = Math.max(len1, len2);
//判断长度
if (len > end - start) {
start = i - (len - 1) / 2;
end = i + len / 2;
}
}
return s.substring(start, end + 1);
}
/**
*
* @param s
* @param left
* @param right
* @return 返回-1， 0， 长度
*/
private int expandAroundCenter(String s, int left, int right) {
int L = left, R = right;
//一直判断
//L >= 0左边不超出去，R < s.length()右边不超出去，
while (L >= 0 && R < s.length() && s.charAt(L) == s.charAt(R)) {
L--;
R++;
}
return R - L - 1;
}
Manacher’s Algorithm 马拉车算法
马拉车算法：查找一个字符串最长回文子串的线性方法
时间复杂度：for 循环里边套了一层 while 循环，难道不是O(n^2)？
不！其实是 O(n)。不严谨的想一下，因为 while 循环访问 R 右边的数字用来扩展，
也就是那些还未求出的节点，然后不断扩展，而期间访问的节点下次就不会再进入 while 了，
可以利用对称得到自己的解，所以每个节点访问都是常数次，所以是 O(n)。
空间复杂度：O(n)。
步骤：
1、
首先我们解决下奇数和偶数的问题，在每个字符间插入 “#”，并且为了使得扩展的过程中，
到边界后自动结束，在两端分别插入 “^” 和 “$”，两个不可能在字符串中出现的字符，
这样中心扩展的时候，判断两端字符是否相等的时候，如果到了边界就一定会不相等，从而出了循环。
经过处理，字符串的长度永远都是奇数了。
2、
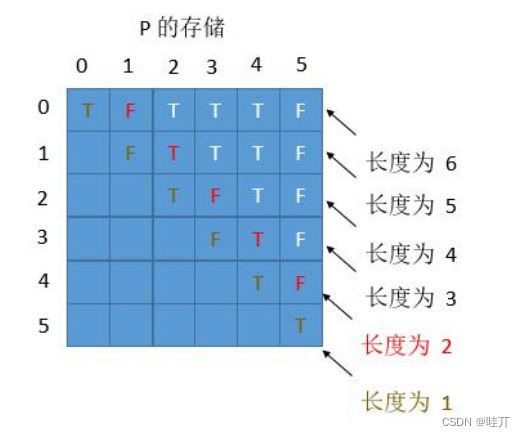
首先我们用一个数组 P 保存从中心扩展的最大个数，而它刚好也是去掉 “#” 的原字符串的总长度。例如下图中下标是 6 的地方，可以看到 P[ 6 ] 等于 5，所以它是从左边扩展 5 个字符，相应的右边也是扩展 5 个字符，也就是 “#c#b#c#b#c#”。而去掉 # 恢复到原来的字符串，变成 “cbcbc”，它的长度刚好也就是 5。
3、求原字符串坐标
用 P 的下标 i 减去 P [ i ]，再除以 2，就是原字符串的开头下标了。
例如我们找到 P[ i ] 的最大值为 5，也就是回文串的最大长度是 5，对应的下标是 6，所以原字符串的开头下标是（6 - 5 ）/ 2 = 0。所以我们只需要返回原字符串的第 0 到 第（5 - 1）位就可以了。
4、求每个p[i]
接下来是算法的关键了，它充分利用了回文串的对称性。
我们用 C 表示回文串的中心，用 R 表示回文串的右边半径。所以 R = C + P[ i ]。C 和 R 所对应的回文串是当前循环中 R 最靠右的回文串。
让我们考虑求 P [ i ] 的时候，如下图。
用 i_mirror 表示当前需要求的第 i 个字符关于 C 对应的下标。
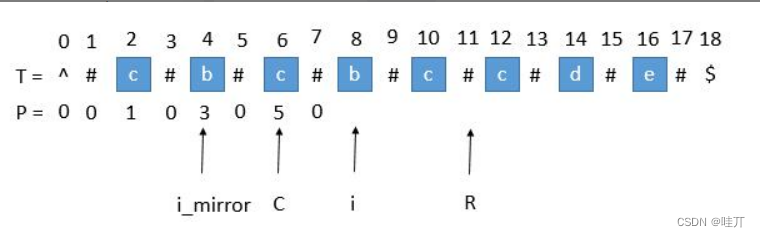
我们现在要求 P [ i ]，如果是用中心扩展法，那就向两边扩展比对就行了。但是我们其实可以利用回文串 C 的对称性。i 关于 C 的对称点是 i_mirror，P [ i_mirror ] = 3，所以 P [ i ] 也等于 3。
但是有三种情况将会造成直接赋值为 P [ i_mirror ] 是不正确的，下边一一讨论。
（1）超出了R
当我们要求 P [ i ] 的时候，P [ mirror ] = 7，而此时 P [ i ] 并不等于 7，为什么呢，因为我们从 i 开始往后数 7 个，等于 22，已经超过了最右的 R，此时不能利用对称性了，但我们一定可以扩展到 R 的，所以 P [ i ] 至少等于 R - i = 20 - 15 = 5，会不会更大呢，我们只需要比较 T [ R+1 ] 和 T [ R+1 ]关于 i 的对称点就行了，就像中心扩展法一样一个个扩展。
（2） P [ i_mirror ] 遇到了原字符串的左边界
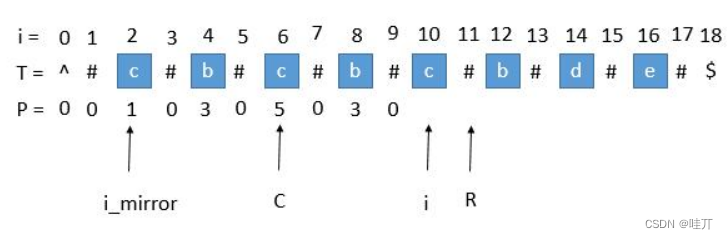
此时 P [ i_mirror ] = 1，但是 P [ i ] 赋值成 1 是不正确的，出现这种情况的原因是 P [ i_mirror ] 在扩展的时候首先是 “#” == “#”，之后遇到了 “^” 和另一个字符比较，也就是到了边界，才终止循环的。而 P [ i ] 并没有遇到边界，所以我们可以继续通过中心扩展法一步一步向两边扩展就行了。
（3）i等于了R
此时我们先把 P [ i ] 赋值为 0，然后通过中心扩展法一步一步扩展就行了。
考虑 C 和 R 的更新
就这样一步一步的求出每个 P [ i ]，当求出的 P [ i ] 的右边界大于当前的 R 时，我们就需要更新 C 和 R 为当前的回文串了。因为我们必须保证 i 在 R 里面，所以一旦有更右边的 R 就要更新 R。
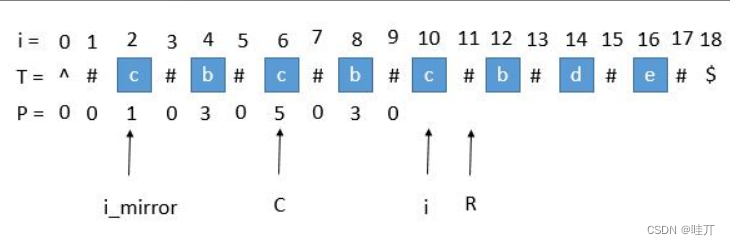
此时的 P [ i ] 求出来将会是 3，P [ i ] 对应的右边界将是 10 + 3 = 13，所以大于当前的 R，我们需要把 C 更新成 i 的值，也就是 10，R 更新成 13。继续下边的循环。
public String preProcess(String s) {
int n = s.length();
if (n == 0) {
return "^$";
}
String ret = "^";
for (int i = 0; i < n; i++)
ret += "#" + s.charAt(i);
ret += "#$";
return ret;
}
// 马拉车算法
public String longestPalindrome2(String s) {
String T = preProcess(s);
int n = T.length();
int[] P = new int[n];
int C = 0, R = 0;
for (int i = 1; i < n - 1; i++) {
int i_mirror = 2 * C - i;
if (R > i) {
P[i] = Math.min(R - i, P[i_mirror]);// 防止超出 R
} else {
P[i] = 0;// 等于 R 的情况
}
// 碰到之前讲的三种情况时候，需要利用中心扩展法
while (T.charAt(i + 1 + P[i]) == T.charAt(i - 1 - P[i])) {
P[i]++;
}
// 判断是否需要更新 R
if (i + P[i] > R) {
C = i;
R = i + P[i];
}
}
// 找出 P 的最大值
int maxLen = 0;
int centerIndex = 0;
for (int i = 1; i < n - 1; i++) {
if (P[i] > maxLen) {
maxLen = P[i];
centerIndex = i;
}
}
int start = (centerIndex - maxLen) / 2; //最开始讲的求原字符串下标
return s.substring(start, start + maxLen);
}
参考：
作者：windliang
链接：https://leetcode.cn/problems/longest-palindromic-substring/solutions/9001/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-bao-gu/
来源：力扣（LeetCode）
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
