膨胀卷积（空洞卷积）

Lin-Fighting

已于 2024-11-11 14:22:06 修改

阅读量2.3k

点赞数 26

文章标签：深度学习人工智能计算机视觉机器学习学习

于 2024-11-11 14:21:23 首次发布

本文链接：https://blog.youkuaiyun.com/weixin_62665562/article/details/143683725

版权

膨胀卷积

介绍

膨胀卷积又叫空洞卷积，最初的提出是为了解决图像分割的问题，常见的图像分割算法通常使用池化层和卷积层来增加感受野(Receptive Filed)，同时也缩小了特征图尺寸，然后再利用上采样来还原图像尺寸，特征图缩小再放大的过程造成了精度上的损失，因此需要一种操作可以再增加感受野的同时保持特征图的尺寸不变，从而代替下采样和上采样操作。

英文: Dilated convolution (Atrous convolution)

作用

增大感受野
保持原输入特征图W、H

计算过程

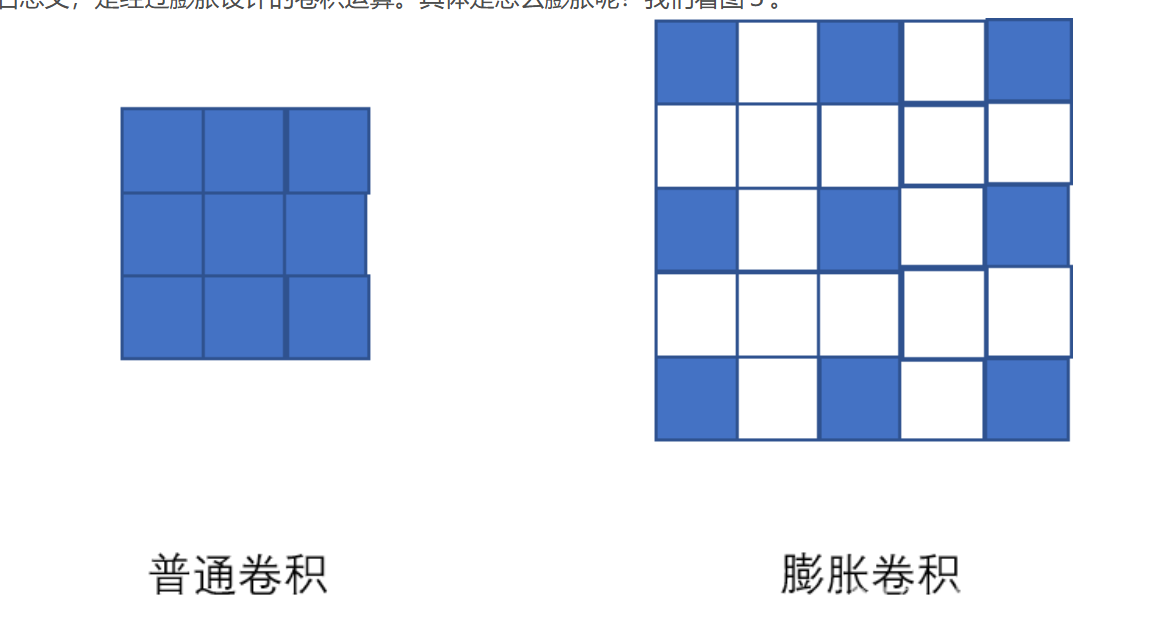
kernel_size = 3, dilation=2

在卷积核每行每列之间插入dilation-1的间隔，这些间隔在实际做卷积时不纳入运算。

dilation=1时为普通卷积

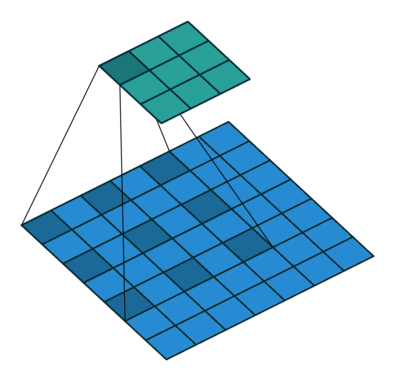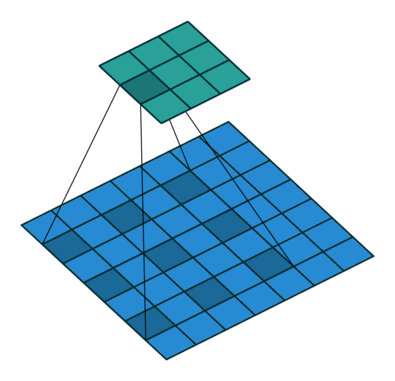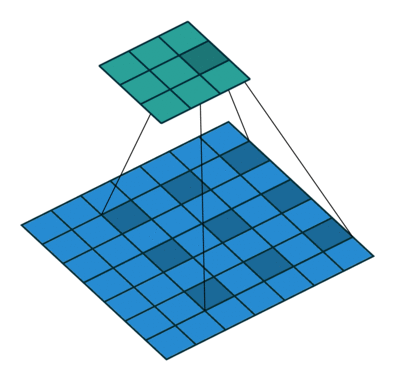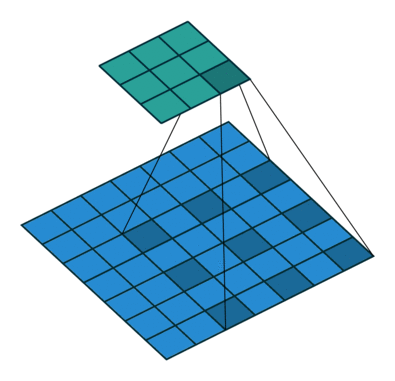
dilation

Pytorch代码使用

# Dilated Conv
conv5 = nn.Conv2d(in_channels=3, out_channels=10, kernel_size=2, dilation=2)
input = torch.randn(1, 3, 30, 30)
output = conv5(input)
print("dilated conv kernel_size 2 dilation 2:", output.shape)


# Dilated Conv
conv6 = nn.Conv2d(in_channels=3, out_channels=10, kernel_size=3, dilation=2)
input = torch.randn(1, 3, 30, 30)
output = conv6(input)
# (1, 10, 26, 26)
print("dilated conv kernel_size 3 dilation 2:", output.shape)

# Dilated Conv
conv7 = nn.Conv2d(in_channels=3, out_channels=10, kernel_size=3, dilation=3)
input = torch.randn(1, 3, 30, 30)
output = conv7(input)
# (1, 10, 4, 24)
print("dilated conv kernel_size 3 dilation 3", output.shape)

# Dilated Conv
conv8 = nn.Conv2d(in_channels=3, out_channels=10, kernel_size=4, dilation=2)
input = torch.randn(1, 3, 30, 30)
output = conv8(input)
# (1, 10, 24, 24)
print("dilated conv kernel_size 4 dilation 2:", output.shape)

# Dilated Conv
conv9 = nn.Conv2d(in_channels=3, out_channels=10, kernel_size=4, dilation=3)
input = torch.randn(1, 3, 30, 30)
output = conv9(input)
# (1, 10, 21, 21)
print("dilated conv kernel_size 4 dilation 3:", output.shape)

结果显示

使用过程

使用过程会造成 gridding effect 的问题

假设连续使用三个膨胀卷积，使用kernel_size=3, 膨胀系数为2的卷积层

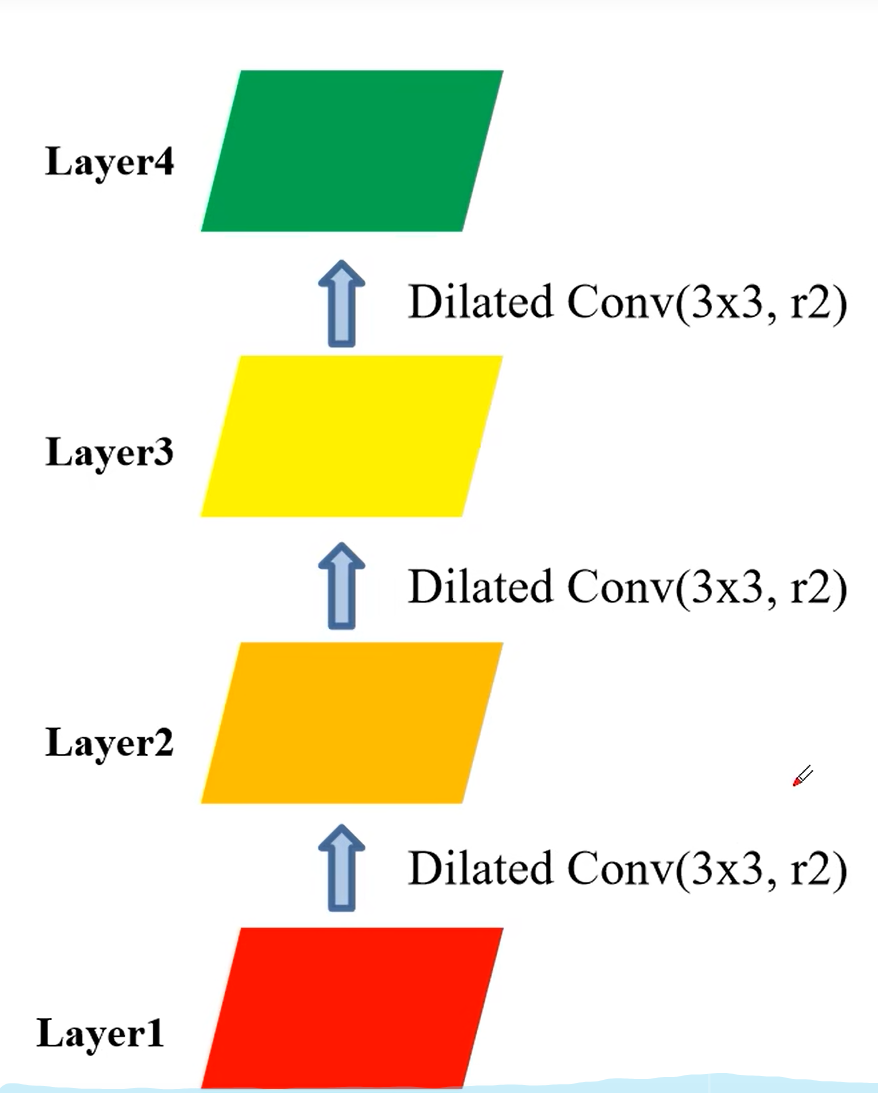
Layer2的一个pixel对应的Layer1信息

Layer3的一个pixel对应的Layer1的信息

Layer4 一个pixel对应Layer1的信息

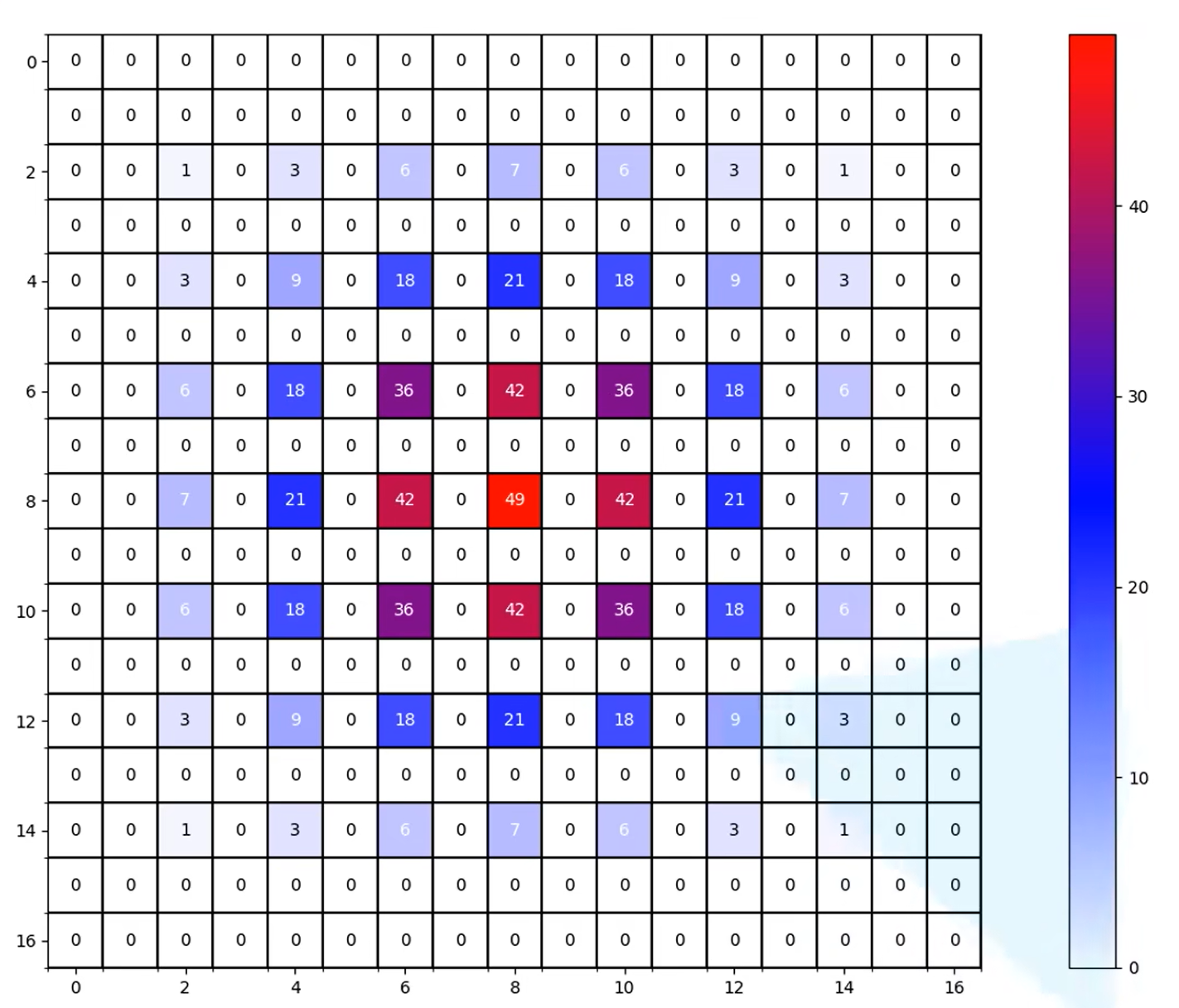
从这里发现Layer4的一个pixel信息对应Layer1的信息不是连续的，这样就造成这个gridding effect的问题。

假设现在将膨胀系数依次改成1、2、3

Layer2的一个pixel信息

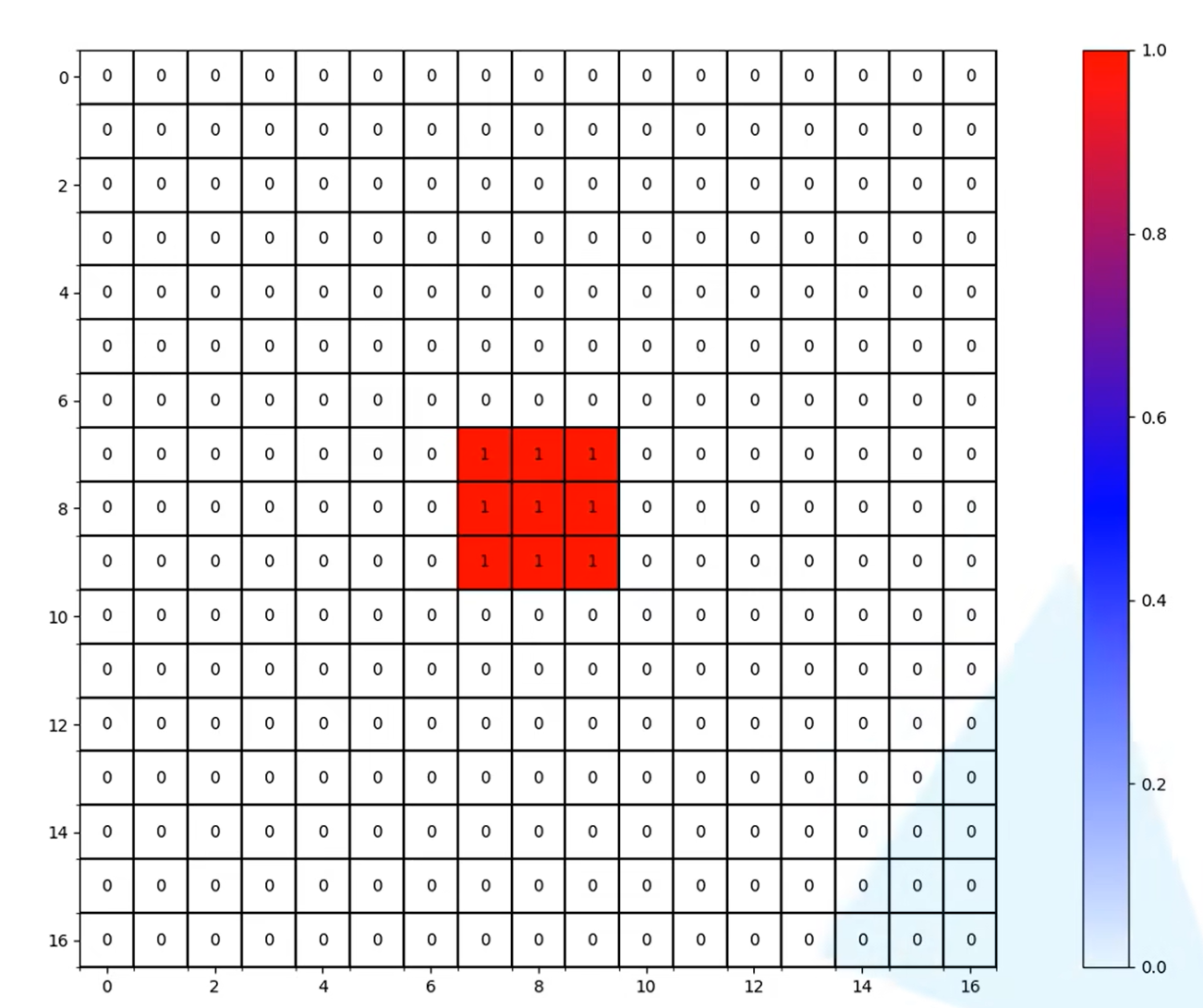
Layer3 一个pixel的信息

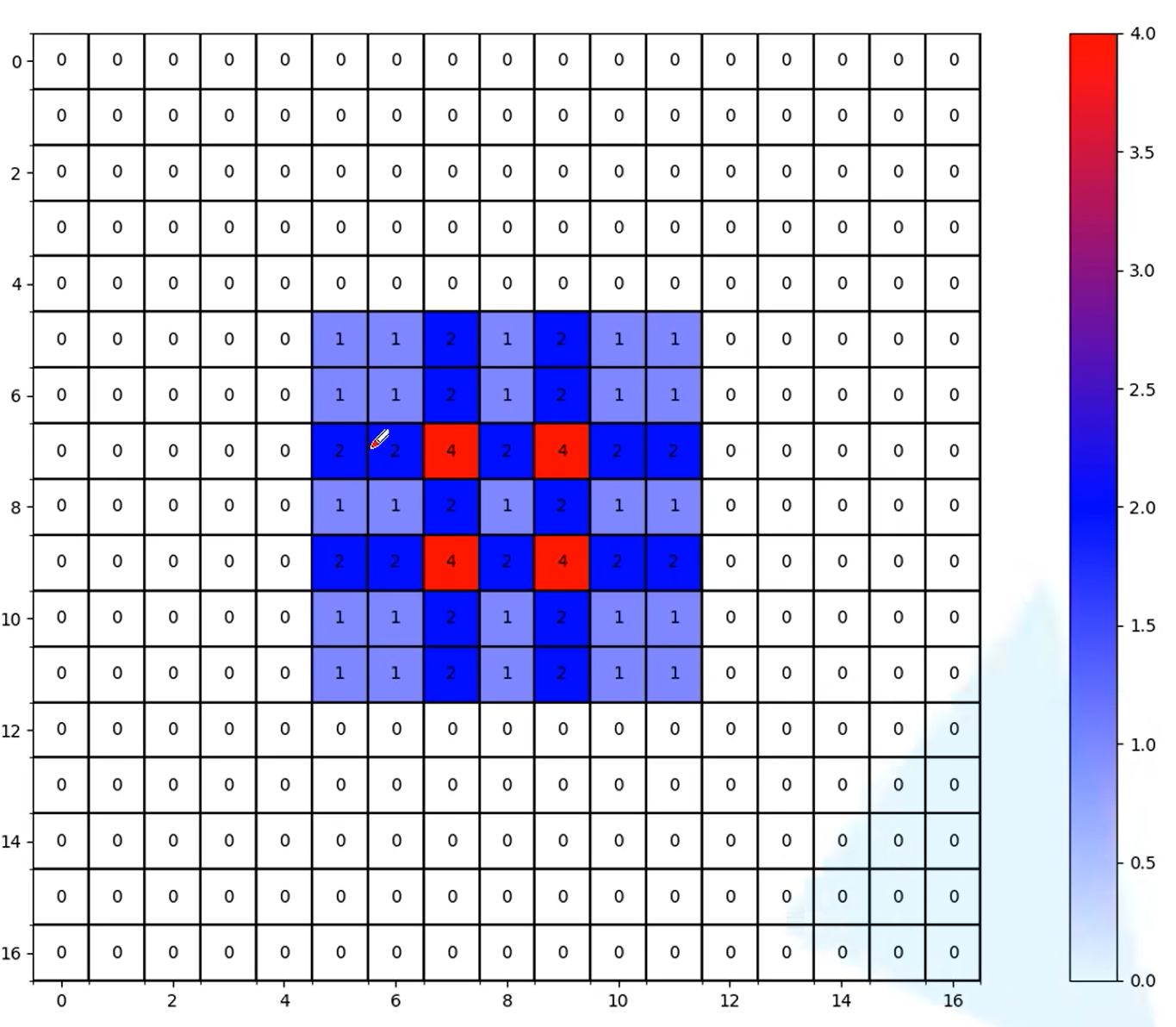
Layer4一个pixel的信息

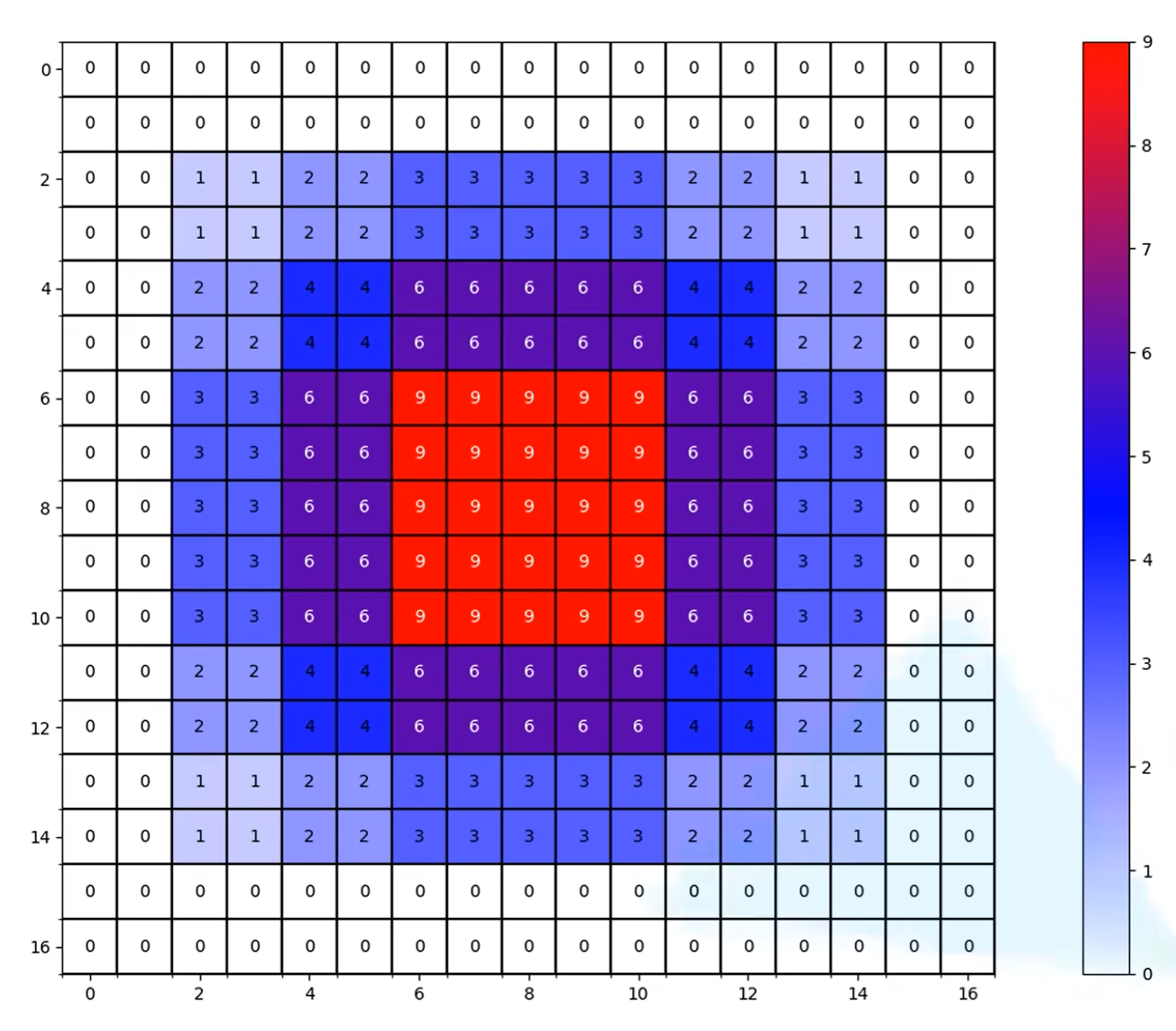
对比可以看出，膨胀系数不同，看到信息的连续性也会不同，实际使用时，更倾向于第二种的膨胀卷积

再对比一下，使用相同系数的普通卷积的效果

普通卷积的感受野也会小一点，可以看出在使用相同参数数量的卷积核时，膨胀卷积能看到的信息会多一点。

如何设计膨胀系数

如何设计

Hybrid Dilated Convolution(HDC)准则

如何设计系数呢，使得最后一层出来的信息都是连续的且之间没有间隙

这里看出一个公式

M(i): 代表第i层的像素之间的距离（如果两个像素在附近则为1，如果两个像素之间间隔一个像素则为2，以此类推）

r(i): 代表第i层的膨胀系数,r=1为普通卷积

K: Kernel_Size的大小

已知: M(n) = r(n)

要使得, M(2) <= K

公式：

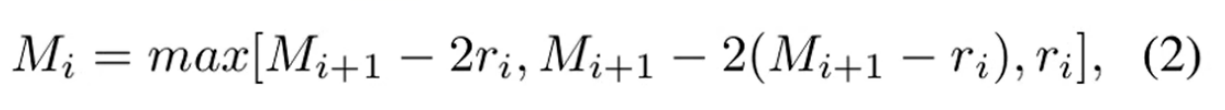
例子1:

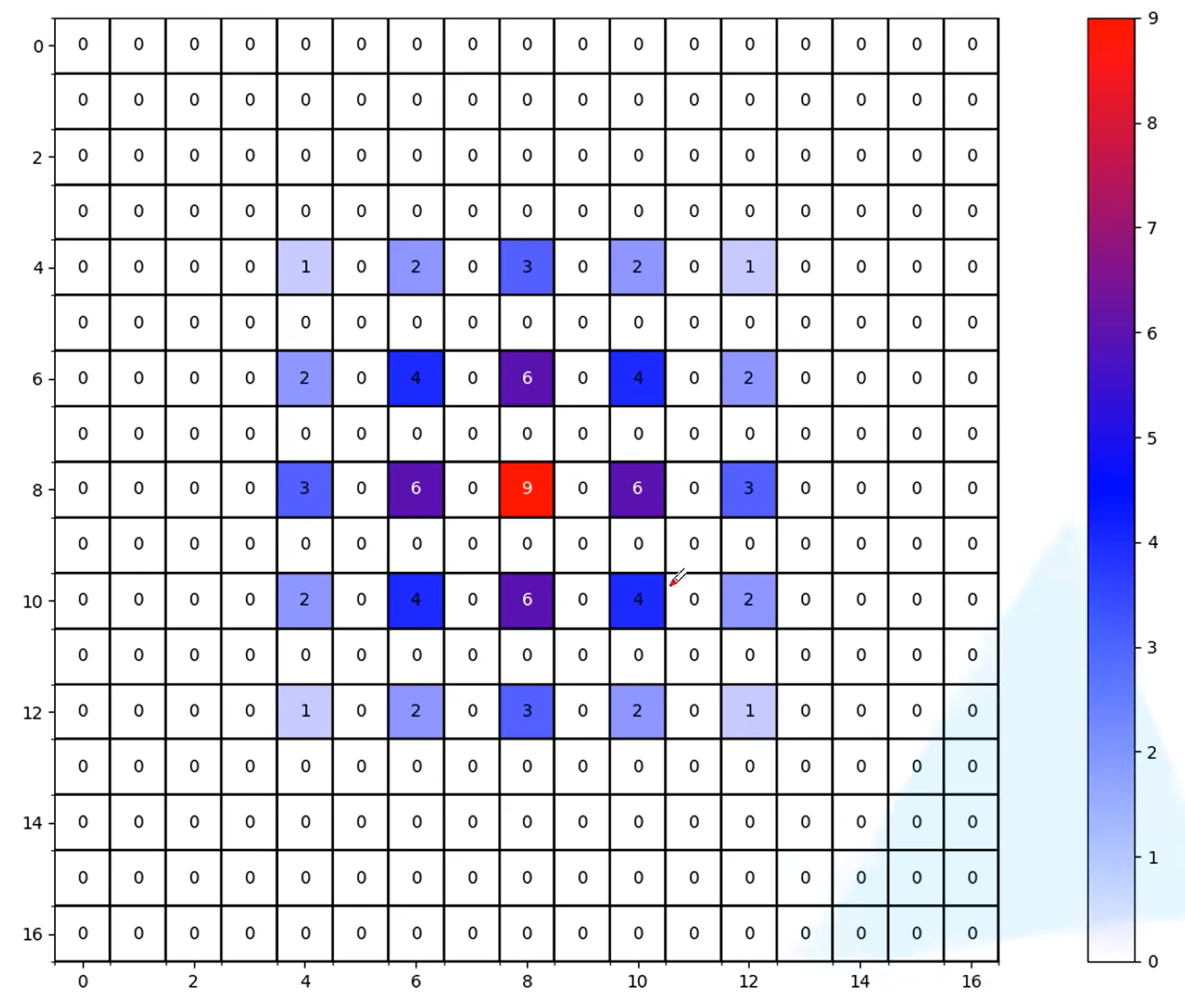
K=3, r=[1,2,5]

根据公式:

M(3) = 5

M(2) = max[M3-2r2, M3-2(M3-r2),r2]

= max(5-4, 5-2*(5-2),2)

= max(1, -1, 2)

= 2 <= 3

符合条件

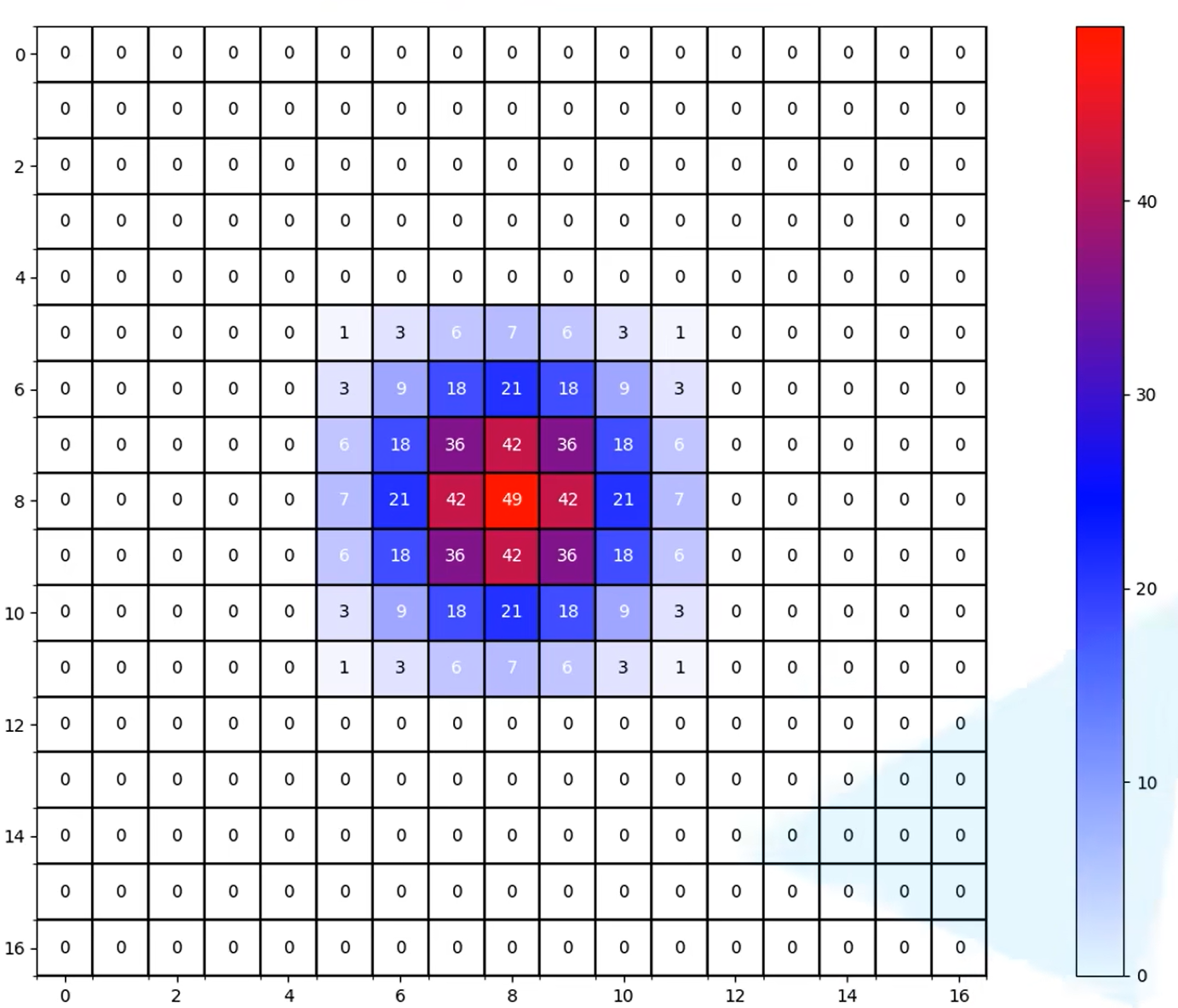
实际效果展示:

代码

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import LinearSegmentedColormap


def dilated_conv_one_pixel(center: (int, int),
                           feature_map: np.ndarray,
                           k: int = 3,
                           r: int = 1,
                           v: int = 1):
    """
    膨胀卷积核中心在指定坐标center处时，统计哪些像素被利用到，
    并在利用到的像素位置处加上增量v
    Args:
        center: 膨胀卷积核中心的坐标
        feature_map: 记录每个像素使用次数的特征图
        k: 膨胀卷积核的kernel大小
        r: 膨胀卷积的dilation rate
        v: 使用次数增量
    """
    assert divmod(3, 2)[1] == 1

    # left-top: (x, y)
    left_top = (center[0] - ((k - 1) // 2) * r, center[1] - ((k - 1) // 2) * r)
    for i in range(k):
        for j in range(k):
            feature_map[left_top[1] + i * r][left_top[0] + j * r] += v


def dilated_conv_all_map(dilated_map: np.ndarray,
                         k: int = 3,
                         r: int = 1):
    """
    根据输出特征矩阵中哪些像素被使用以及使用次数，
    配合膨胀卷积k和r计算输入特征矩阵哪些像素被使用以及使用次数
    Args:
        dilated_map: 记录输出特征矩阵中每个像素被使用次数的特征图
        k: 膨胀卷积核的kernel大小
        r: 膨胀卷积的dilation rate
    """
    new_map = np.zeros_like(dilated_map)
    for i in range(dilated_map.shape[0]):
        for j in range(dilated_map.shape[1]):
            if dilated_map[i][j] > 0:
                dilated_conv_one_pixel((j, i), new_map, k=k, r=r, v=dilated_map[i][j])

    return new_map


def plot_map(matrix: np.ndarray):
    plt.figure()

    c_list = ['white', 'blue', 'red']
    new_cmp = LinearSegmentedColormap.from_list('chaos', c_list)
    plt.imshow(matrix, cmap=new_cmp)

    ax = plt.gca()
    ax.set_xticks(np.arange(-0.5, matrix.shape[1], 1), minor=True)
    ax.set_yticks(np.arange(-0.5, matrix.shape[0], 1), minor=True)

    # 显示color bar
    plt.colorbar()

    # 在图中标注数量
    thresh = 5
    for x in range(matrix.shape[1]):
        for y in range(matrix.shape[0]):
            # 注意这里的matrix[y, x]不是matrix[x, y]
            info = int(matrix[y, x])
            ax.text(x, y, info,
                    verticalalignment='center',
                    horizontalalignment='center',
                    color="white" if info > thresh else "black")
    ax.grid(which='minor', color='black', linestyle='-', linewidth=1.5)
    plt.show()
    plt.close()


def main():
    # bottom to top
    dilated_rates = [1, 2, 5]
    # init feature map
    size = 31
    m = np.zeros(shape=(size, size), dtype=np.int32)
    center = size // 2
    m[center][center] = 1
    # print(m)
    # plot_map(m)

    for index, dilated_r in enumerate(dilated_rates[::-1]):
        new_map = dilated_conv_all_map(m, r=dilated_r)
        m = new_map
    print(m)
    plot_map(m)


if __name__ == '__main__':
    main()

结果

例子2：

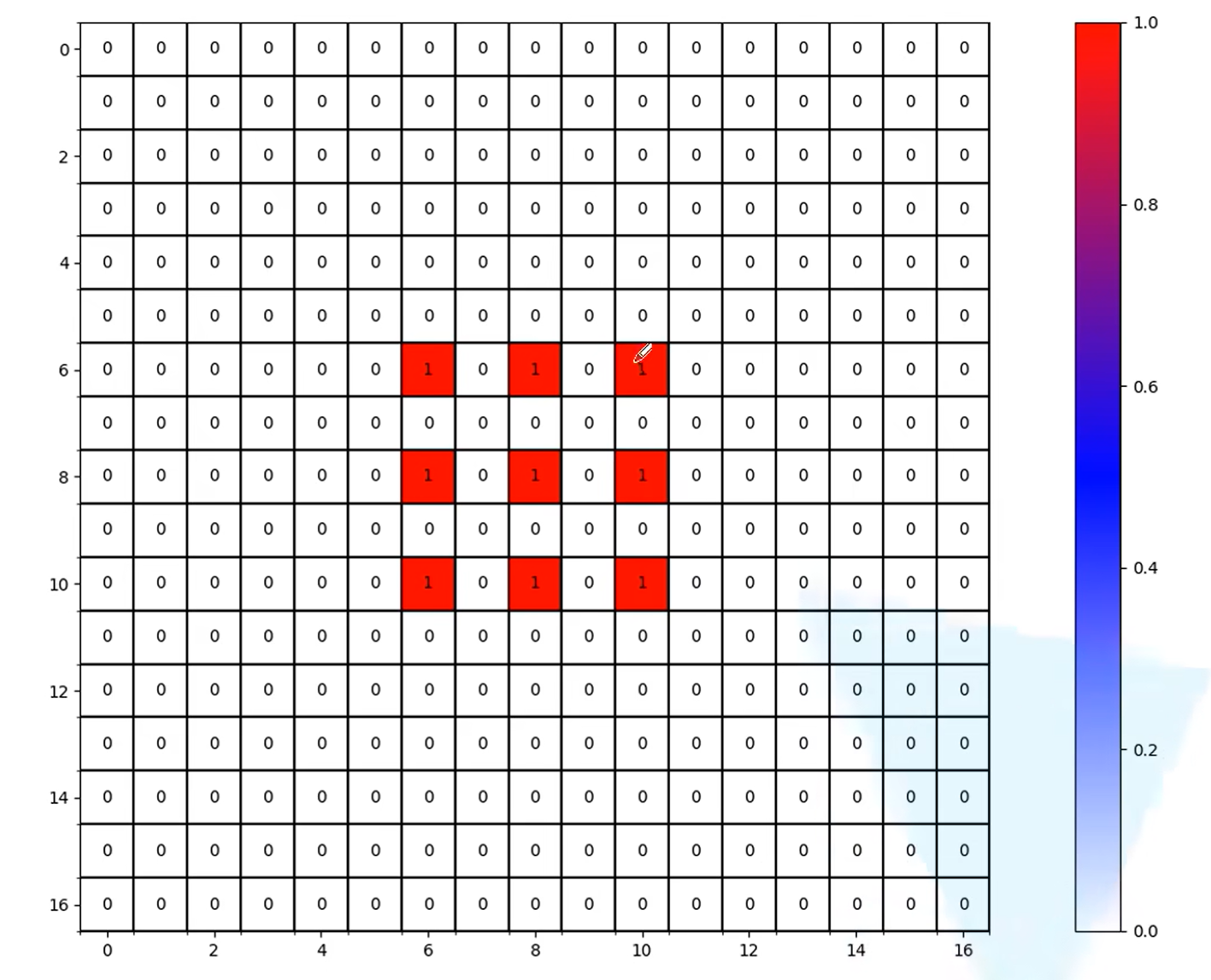
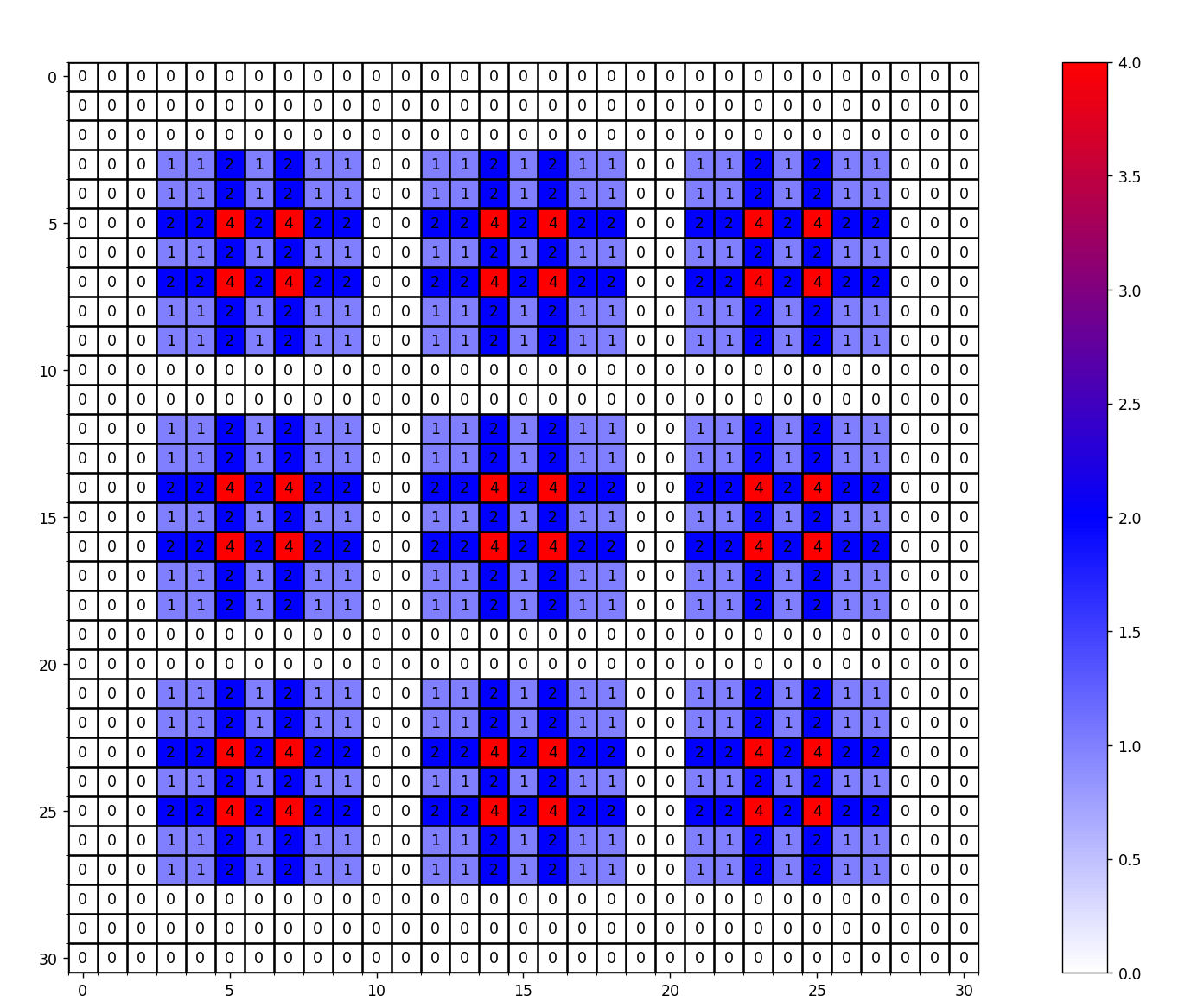
K=3, r=[1,2,9]

根据公式:

M(3) = 9

M(2) = max[M3-2r2, M3-2(M3-r2),r2]

= max(9-4, 9-2*(9-2),2)

= max(5, -5, 2)

= 5 > 3 M(1) = 3, 实际显示两个非零元素之间间隔为2

不符合条件

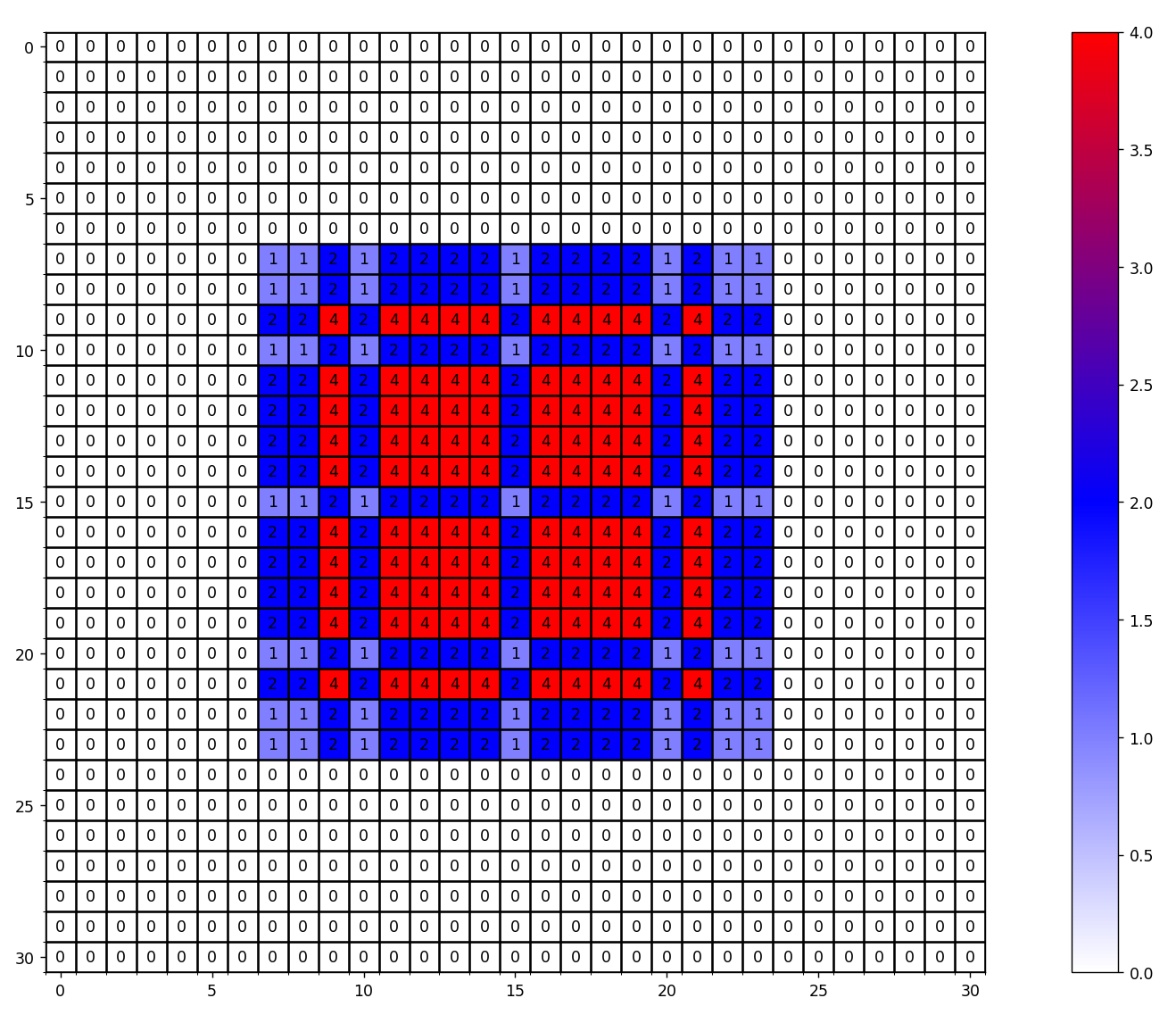
实际效果展示:

代码

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import LinearSegmentedColormap


def dilated_conv_one_pixel(center: (int, int),
                           feature_map: np.ndarray,
                           k: int = 3,
                           r: int = 1,
                           v: int = 1):
    """
    膨胀卷积核中心在指定坐标center处时，统计哪些像素被利用到，
    并在利用到的像素位置处加上增量v
    Args:
        center: 膨胀卷积核中心的坐标
        feature_map: 记录每个像素使用次数的特征图
        k: 膨胀卷积核的kernel大小
        r: 膨胀卷积的dilation rate
        v: 使用次数增量
    """
    assert divmod(3, 2)[1] == 1

    # left-top: (x, y)
    left_top = (center[0] - ((k - 1) // 2) * r, center[1] - ((k - 1) // 2) * r)
    for i in range(k):
        for j in range(k):
            feature_map[left_top[1] + i * r][left_top[0] + j * r] += v


def dilated_conv_all_map(dilated_map: np.ndarray,
                         k: int = 3,
                         r: int = 1):
    """
    根据输出特征矩阵中哪些像素被使用以及使用次数，
    配合膨胀卷积k和r计算输入特征矩阵哪些像素被使用以及使用次数
    Args:
        dilated_map: 记录输出特征矩阵中每个像素被使用次数的特征图
        k: 膨胀卷积核的kernel大小
        r: 膨胀卷积的dilation rate
    """
    new_map = np.zeros_like(dilated_map)
    for i in range(dilated_map.shape[0]):
        for j in range(dilated_map.shape[1]):
            if dilated_map[i][j] > 0:
                dilated_conv_one_pixel((j, i), new_map, k=k, r=r, v=dilated_map[i][j])

    return new_map


def plot_map(matrix: np.ndarray):
    plt.figure()

    c_list = ['white', 'blue', 'red']
    new_cmp = LinearSegmentedColormap.from_list('chaos', c_list)
    plt.imshow(matrix, cmap=new_cmp)

    ax = plt.gca()
    ax.set_xticks(np.arange(-0.5, matrix.shape[1], 1), minor=True)
    ax.set_yticks(np.arange(-0.5, matrix.shape[0], 1), minor=True)

    # 显示color bar
    plt.colorbar()

    # 在图中标注数量
    thresh = 5
    for x in range(matrix.shape[1]):
        for y in range(matrix.shape[0]):
            # 注意这里的matrix[y, x]不是matrix[x, y]
            info = int(matrix[y, x])
            ax.text(x, y, info,
                    verticalalignment='center',
                    horizontalalignment='center',
                    color="white" if info > thresh else "black")
    ax.grid(which='minor', color='black', linestyle='-', linewidth=1.5)
    plt.show()
    plt.close()


def main():
    # bottom to top
    dilated_rates = [1, 2, 9]
    # init feature map
    size = 31
    m = np.zeros(shape=(size, size), dtype=np.int32)
    center = size // 2
    m[center][center] = 1
    # print(m)
    # plot_map(m)

    for index, dilated_r in enumerate(dilated_rates[::-1]):
        new_map = dilated_conv_all_map(m, r=dilated_r)
        m = new_map
    print(m)
    plot_map(m)


if __name__ == '__main__':
    main()

结果