n层台阶，一次跳1层或者2层，总共有多少种跳法

在某厂面试中遇到这个问题，当时被n个台阶困扰，感觉无从下笔。面试过后又静下心来思考，发现自己搞错了重点。问题重点是几种跳法，而不是几阶台阶。这样问题就变成：假如有5层台阶，一次跳1层或者2层，总共有多少种跳法？

分析

假设用方法f(n)来求取总共多少种跳法，n为台阶总数。那么5层台阶的跳法就是f(5)，第一次跳，可能跳1层或者2层，那么f(5)=1+f(4)或者2+f(3)；第二次跳，也可能跳1层或者2层，那么f(4)=1+f(3)或者2+f(2)；f(3)=1+f(2)或者2+f(1)；f(2)=1+f(1)或者2+f(0)；f(1)=1+f(0)；当台阶数n=0时，总共跳法f(0)=0。可以得到f(5)=8，f(4)=5，f(3)=3，f(2)=2，f(1)=1；可以看出f(5)=f(4)+f(3)，f(4)=f(3)+f(2)，f(3)=f(2)+f(1)。即可以得出f(n)=f(n-1)+f(n-2)，当总台阶数n=1或2时不适用该公式；当总台阶数n=1时，只有跳1层台阶1种跳法，总跳法f(1)=1，当总台阶数n=2时，有1+1和2两种跳法，总跳法f(2)=2；那么当台阶数n=1或者n=2时就是程序的出口。能够看出这是一个斐波那契数列，可以得到：

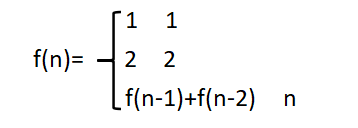
实现

所以这里需要使用递归，完整代码如下：

    //青蛙跳台阶  一次可以跳1阶或者2阶
    public static void main(String[] args) {
        int num = 5;
        System.out.println("递归青蛙"+num+"级台阶共有"+f1(num)+"种方法！");
        System.out.println("非递归青蛙"+num+"级台阶共有"+f2(num)+"种方法！");
    }

    //递归方式
    /*if(n==1||n==2)
    * 1. n=5 return f1(4)+f1(3)
    * 2. 进入第1步的f1(4) return f1(3)+f1(2)
    * 3. 进入第2步的f1(3) return f1(2)+f1(1)
    * 4. 进入第3步的f1(2) return 2
    * 5. 进入第3步的f1(1) return 1
    * 6. 进入第2步的f1(2) return 2
    * 7. 进入第1步的f1(3) return f1(2)+f1(1)
    * 8. 进入第7步的f1(2) return 2
    * 9. 进入第8步的f1(1) return 1
    * 10.return 2+1+2+2+1=8
    * */
    public static int f1(int n){
        if(n==1||n==2){
            System.out.println("n="+n);
            return n;
        }else{
            System.out.println("n="+n);
            return f1(n-1)+f1(n-2);
        }
    }

    //动态规划方式
    public static int f2(int m){
        if(m==1||m==2){
            return m;
        }

        int a1 = 1;
        int a2 = 2;
        int result = 0;
        for (int i = 3; i <= m; i++){
            result = a1 + a2;
            a1 = a2;
            a2 = result;
        }
        return result;
    }

斐波那契查找拓展

斐波那契查找算法