跟着李沐老师学习深度学习（四）

多层感知机

感知机

• 给定输入x，权重w，和偏移b，感知机输出：
  
  本质是一个二分类问题。（离散的类）

  • vs.线性回归输出的是实数
  • vs.softmax回归输出的是概率

• 训练感知机（60年代）：
  

  • 等价于使用批量大小为1的梯度下降，并使用如下的损失函数：
    
    max() 对应if语句；如果分类正确，则y > 0，所以loss = 0 — >不作更新。

• 收敛定理

  • 假设数据在一个半径 r 内的区域里；假设存在一个余量为 ρ 的分截面，使得所有的分类都是正确的。
    
    在以上情况下，可以知道感知机确实能找到一个最优解，并保证只会在 （r^2 + 1）/ ρ^2 步后收敛。

• XOR问题（Minsky & Papert, 1969）

  • 感知机不能拟合XOR函数，只能产生线性分割面。（不管怎么切，都不能分隔开）

之后，找到了该问题的解决方法——多层感知机

• 总结
  • 感知机是一个二分类模型，是最早的AI模型之一
  • 它的求解算法等价于使用批量大小为1的梯度下降
  • 它不能拟合 XOR 函数（第一次 AI 寒冬）

多层感知机

• 学习XOR
  想要完全分类，单是线性分类是不行的，解决步骤：

  • 学习两种感知机，如下图中蓝色和黄色的线
  • 然后使用两种结果进行相乘，得到的结果我们就可以进行分类（如下表）
    
    
    
    一次做不了，就先学一个简单的模型，然后在学一个，共同解决一个复杂问题 —— 即：多层感知机解决的问题。

• 单隐藏层
  简单的讲，就是下面这个图：（隐藏层大小是超参数）
  

• 单隐藏层——单分类
  其中，m：是隐藏层的神经元个数（h1 ~ h5）；n：是样本的特征数（x1 ~ x4）
  
  其中，σ是按元素的激活函数

• 为什么需要非线性激活函数？
  常犯错误：没有加激活函数，即：当我们将n个全连接层放在一起，发现还是一个最简单的线性模型。

• 激活函数：

  • Sigmoid()激活函数：对于一个定义域在R中的输入，将输入变换为区间(0, 1)上的输出
    
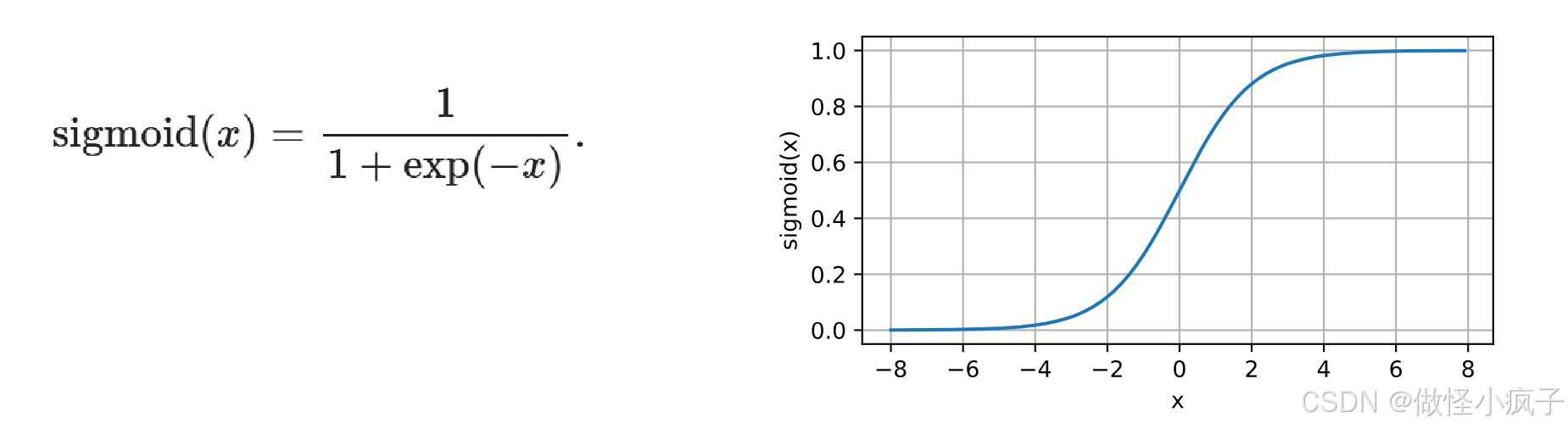
  • Tanh激活函数： 将输入投影到（-1，1）
    
  • RelU激活函数（rectified linear unit）
    
    该函数比较常用、简单。

• 多类分类