数据分析师25-统计学知识

假设检验及例题讲解_学渣渣渣渣渣的博客-优快云博客_假设检验例题

1:如何判断数据的离散程度

2:总体均值的区间估计=平均值+-（z 阿尔法/2）*标准差/根号样本量。（）里面 只有小样本且方差未知的情况，我们用t值（n-1）的表，其余都是z检验。 

3:根据上面公式 误差error=平均值+-（）*标准差/根号样本量。现实中取样本的量肯定不是越多越好 涉及到成本，也不能太少，所有会根据 我们能接受的error大小 反推出样本应该取多少。error一般是10%的误差。

4:假设检验的逻辑是： 样本数据 估计总体 。样本的区间就是平均值+-（z 阿尔法/2）*标准差/根号样本量，如果 我们假设的值 在这个样本的区间内，那就假设成立了。如果原假设的不在这个区间，那就拒绝原假设。

或者用数学的方式直接告诉你要不要拒绝：把假设的值 放到 公式里面：

（样本平均值-假设值）/（样本标准差/根号样本量） 如果这个Z 阿尔法/2 过大/过小 就说明假设值发生的概率很小 拒绝。

5:但是由于我们样本可能是不对的，所以

：type 2如果我们要验证的那个值 在样本区间 反而不应该 接受他 因为他本来就是错误的 求伪

：type 1如果我们要验证的那个值 不在样本区间 反而不应该拒绝他 因为他本来是对的 弃真 5%

6:假设验证的应用

：我现在想看我的活动有没有显著提升，也就是想看B组的数据有没有显著高于A（是一个单一数值）怎么看？就是：A的值放进B组平均值和标准差的公式里 ，求出 Z阿尔法/2 看看是不是过大过小。

7:两个总体之间平均值之差的检验，这个更常用一些（这个公式适用于总体方差已知 但是通常不可能知道的！！！所以一般用t检验。！！ ）

：比如我想比较空白组A和实验组B 想证明实验组B是显著有效果的，要高于空白组A。也就是B做了一些策略，想证明策略是有用的。其实就是比较AB组的平均值是否相等 样本数量足够大 默认是服从正态分布的。直接放到公式即可：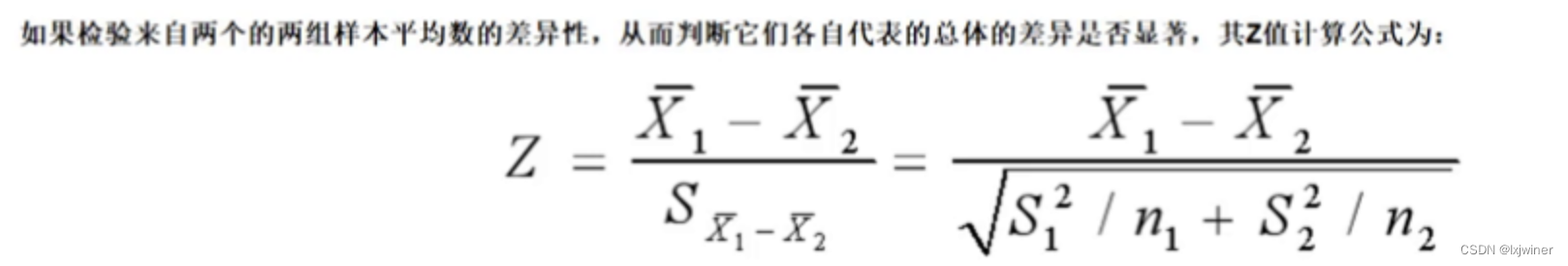

如果方差未知的话 就需要用t检验，！！在t检验之前，需要判断2个总体的方差是否一样？所以涉及到（F检验），如果F检验显示不显著，就一般双样本t检验，如果显著就非参数t检验

：简单的F检验）就是比较两组数据的方差是不是一致的，应用该场景就是评价策略有没有带来影响 AB数据的放出是否显著有差异。

直接算出AB组的方差， 一除 然后查看看对应n-1正常的范围即可。判断是否显著不同

检验完毕后，才是t检验

：这里补充说明一下区别三种T检验的详细区分_spssau的博客-优快云博客_t检验的三种类型和应用条件

1:独立样本t检验就是一般的检验，用户两组数据的对比。可以用于对照实验，也可以单纯的单因素分析。

2:配对样本检验需是严格条件下的独立样本t检验，需要数据2列 一一对应的关系，数量一致，最多用于对照和实验。

3：如果多因素或者多组数据了，那就是方差分析。

4:如果x y 都是定性的 那就是卡方检验

8:有难度的F检验：适用于多组数据之间的比较 具体应用场景：比如我想看ABCD组数据，每组的数据是否是显著有差异的？？什么意思？？
ABCD组数据可能存在差异 是因为有一个变量X因子，F检验（方差分析）的目的就是想证明X 是否对数据有显著影响。 多个因素就是方差分析，2个就是F检验或者t检验

ABCD数据有差异=组内误差总和+组外误差总和。如果组外误差/组内误差 很大，则说明X因子有显著影响。

比如ABCD每组6个数 一共24个数

组内方差总和：（A组每个数- A组平均值）的平方 X 6 + 同理B +C+D

组外：（所有数24个数的平均值- A组平均值）的平方 X 6 （其实就是几个数加几回），+B组同样的计算方式 + C+ D。 求和即可。     

9:卡方检验，适用的场景 也是 看 X因子对 A B组数据有没有影响 但是和F检验的差别在于：卡方只看最终结果的占比，来判断真实值和理论值 之间的差异。比如有4群人

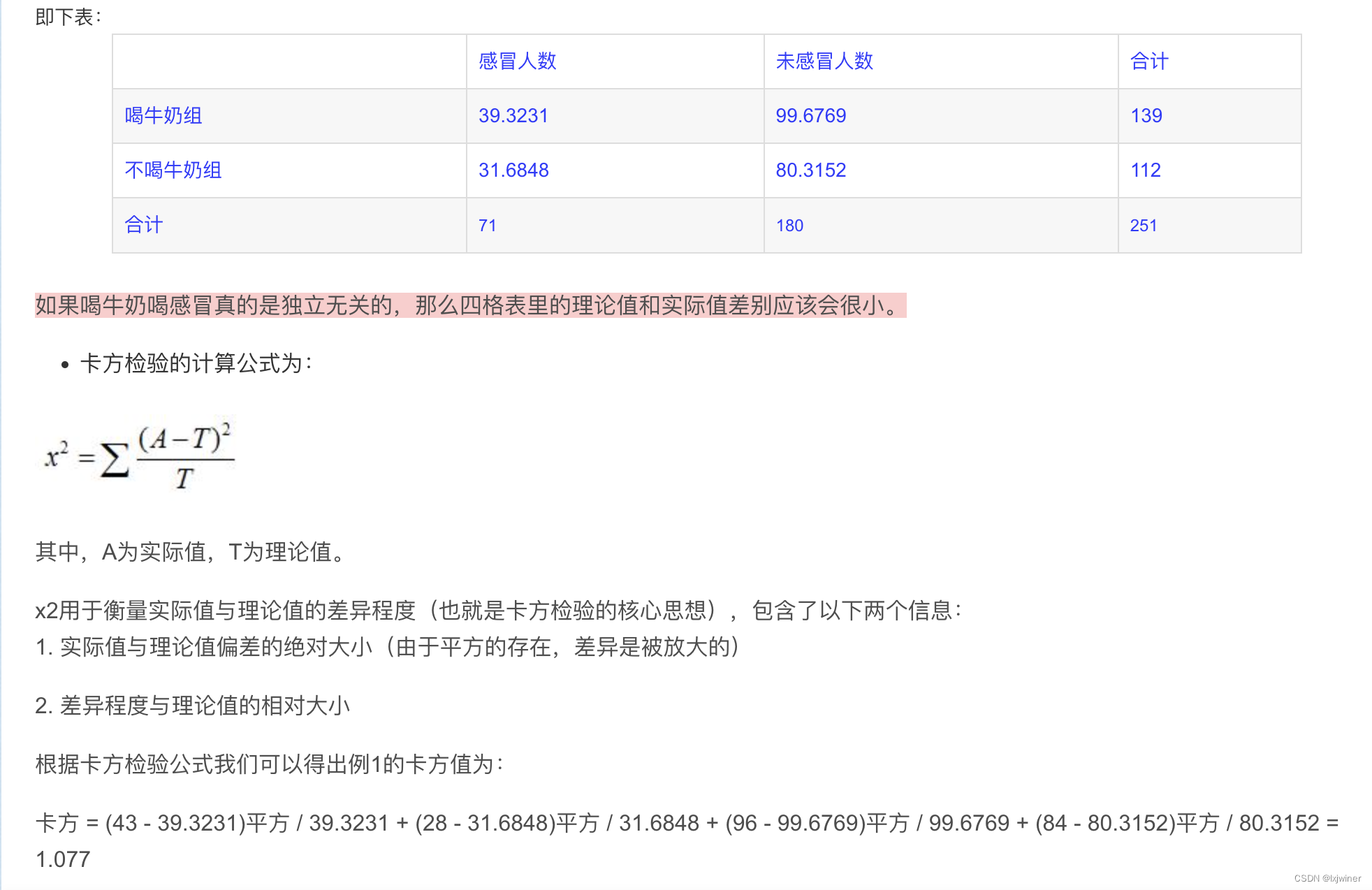
10:AHP层次分析法

层次分析法(AHP) - 知乎

11:熵权法

如何用熵权法计算权重？ - 知乎

12:用excel做假设检验和方差分析

可重复的理解：首先是多维度的，那如果在某个（多维度结合）场景下，样本数据量如多于1组，就代表着样本是重复的，需要对这个特点场景进行一次计算，然后才是组内和组外。

可重复：

无重复：

 

 

Excel 如何实现方差分析：单因素、包含重复的双因素、无重复的双因素方差分析_office教程

13:用python做假设检验和方差分析