机器学习-总结笔记-集成学习-Bagging/Boosting/Stacking

最新推荐文章于 2025-05-06 17:42:05 发布

Toooooopia

最新推荐文章于 2025-05-06 17:42:05 发布

阅读量320

点赞数

CC 4.0 BY-SA版权

分类专栏：机器学习文章标签：机器学习

本文链接：https://blog.youkuaiyun.com/weixin_52329576/article/details/117905653

机器学习专栏收录该内容

5 篇文章

订阅专栏

本文深入探讨集成学习的概念，通过‘三个臭皮匠赛过诸葛亮’的比喻解释其原理。详细介绍了Boosting系列的AdaBoost、GBDT和XGBoost，强调它们如何通过组合弱分类器提升整体性能。AdaBoost着重于权重调整，GBDT通过拟合梯度提升，XGBoost则优化目标函数以避免过拟合。同时，还提及了并行训练的Bagging方法，特别是随机森林的应用。最后，讨论了Stacking的两阶段学习过程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

作业大概是学生时代激发自主学习的最好动力，但商科人啃ML真是要哭了T_T。也是实在看公式费力的很，基于自己易理解的角度，能文字表述的都转文字表述了（商科人的无奈）。

文章目录

集成学习

集成学习

我理解的集成学习就好比是“三个臭皮匠赛过诸葛亮”。利用多个学习器使得最终精度越来越高。
即，一堆弱分类器组合起来使得最终结果更好。

Boosting——‘串行’

思路：

根据数据集训练1st 学习器
1st 学习器分类错误的样本数据的权重会被调整
基于调整后的权重再训练2nd 学习器
依此原则不断训练，直到学习器数量达到设定值，再将这些学习器进行加权结合

AdaBoost

思路：针对二分类任务

如有N个数据，则初始每个数据的权重都为1/N
选择误差率最低的分类点定为1st 学习器，此时1st 学习器的错误率为e【如十个样本此时每个样本的权重为0.1，正确分类8个、错误分类2个，错误率即为0.1+0.1 = 0.2】
代入公式α = 1/2 * log[(1 - e) / e] 作为1st 学习器的权重
根据刚错误分类的数据点进行数据点的权重调整，新数据点权重 = 原数据点权重 * exp（-学习器权重 * 数据点正负例 * 学习器将此分类点分为正负例)所占总体数据点累加和的权重
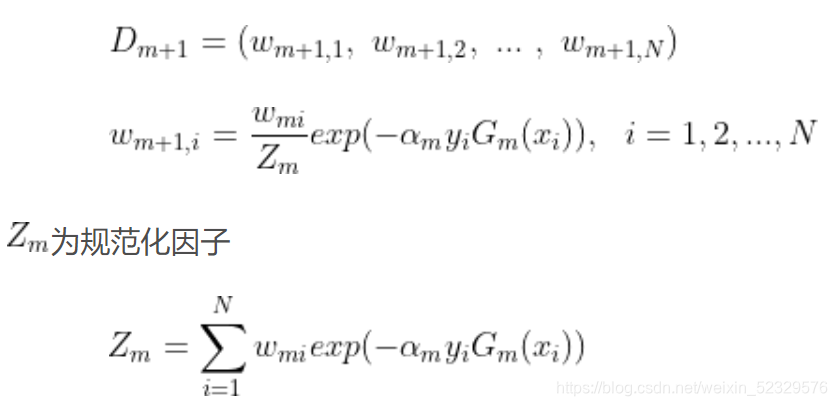
【repeat】选择此时误差率最低的分类点定位2nd 学习器，重复上述步骤，直到设定的学习器的数量T
将T个学习器的权重乘以其对应的二分类学习器再取sign函数即为最终的学习器：
G(x) = sign[α1 * G1(x) + α2 * G2(x) + … + αt * Gt(x)]

GBDT

[说句闲扯的，每次看到GBDT脑子里总是韩剧韩综报电视台名的配音Hhhhh 神奇]

每个弱分类器去拟合上一个分类器的误差函数对预测值的梯度/残差(这个梯度/残差就是预测值与真实值之间的误差)，最后所有弱分类器的结果相加等于预测值。

XGBoost

可以与决策树另一篇博客：决策树相关联系起来。

举个栗子先：
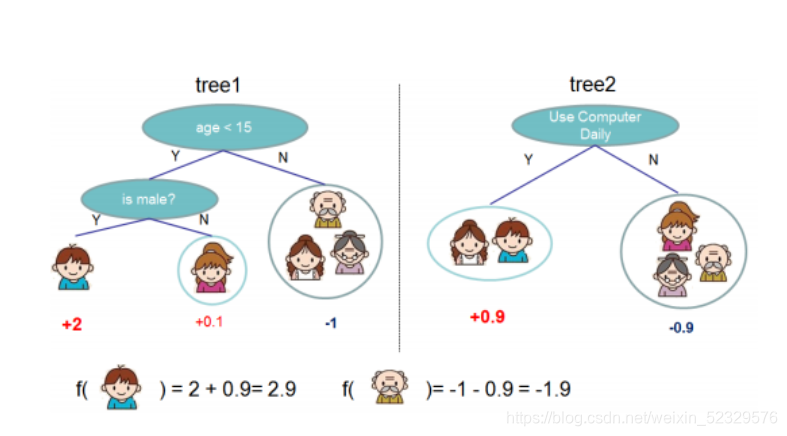
在这里插入图片描述
上图是两个决策树，我们想知道这五个人是否喜欢玩电子游戏：现已每个人都分到了一个叶子节点中，现在对这些叶子节点一些权重项（其中正数代表喜欢玩，负数代表不喜欢玩），接下来将权重值和叶子节点进行一个结合，综合评判当前的人是否喜欢玩游戏；而多棵决策树可以集成起来提升整体学习器的效果。

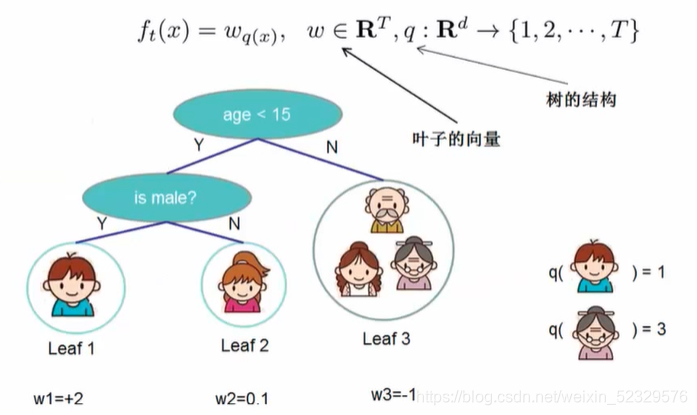
XGBoost 原理

每个叶子节点的预测值=该样本*叶子节点权值
在这里插入图片描述
此处目标函数使用均方误差，且代表损失函数，我们的目的就是使得目标函数最小化。

那如何求得最小化的目标函数？

将手里的样本都去求损失值
再将这些损失值求一个均值，所以相当于算了一个期望值
再求解期望值的最小值

而且XGBoost是多个决策树的集成算法，所以每棵树的结果都会对最终的结果产生影响。

在这里插入图片描述
核心思想：**就是通过加树的方式使整体效果提升~**所以每加一棵树意味着在上一次的预测值的基础上加了一个function，但也要保证整体表达效果在提升，即目标函数在下降。

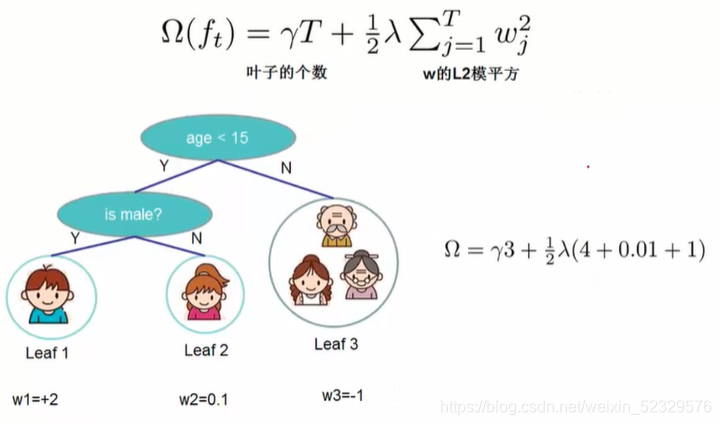
在这里插入图片描述

由于决策树叶子节点过多极有可能造成过拟合，所以我们限制其叶子节点的个数，如上图所示的 Ω 即为惩罚项。（叶子节点个数越多，惩罚的力度越大）

我们的目标函数变成了原先的均方误差+正则化惩罚项 Ω(ft)。
在这里插入图片描述
可以看出我们的Obj是所有树的均方误差目标函数和正则化惩罚项的加总。constant代表计算过程中产生的常数项。

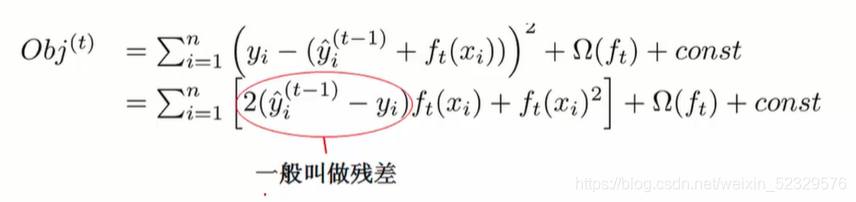
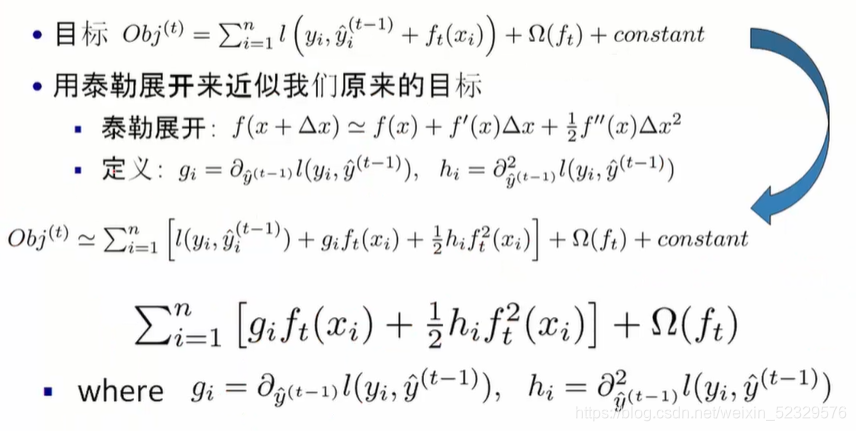
即，g代表一阶导、h代表二阶导。

n为样本个数、T为叶子节点个数。
ft 即为每个叶子的权重项*样本落在哪个叶子节点上。
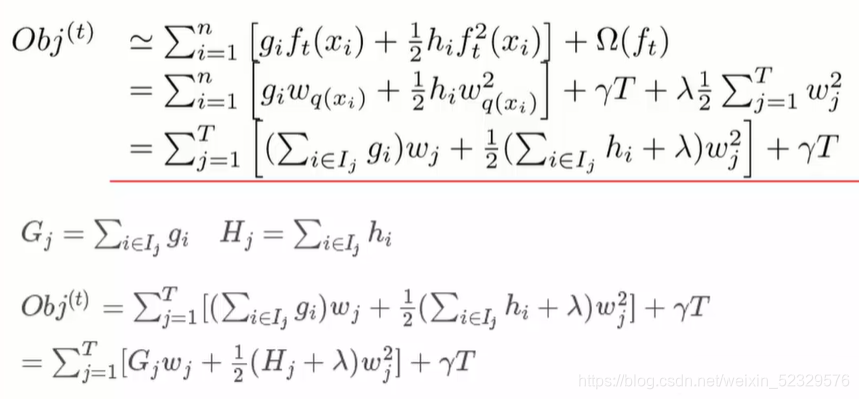
在这里插入图片描述

通过求偏导的方式解得最小目标函数。

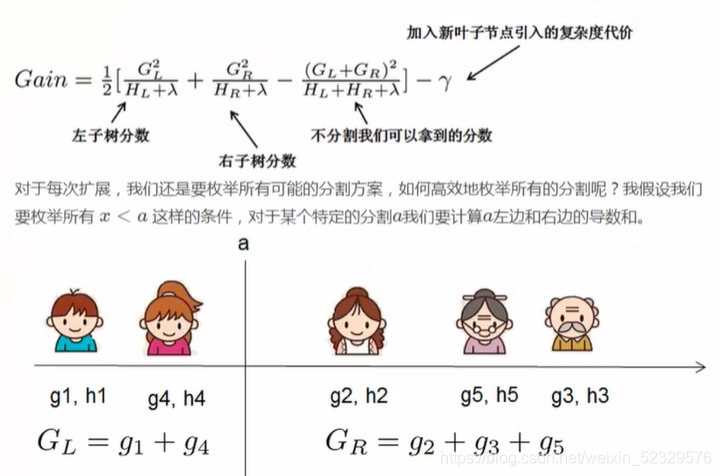
gain增益：分割之后的分数 - 没分割之前的分数。
哪个增益大，就在哪里分割。

Bagging——‘并行’

Bagging ：bootstrap aggregation（并行训练多个分类器）
最典型的代表：随机森林
① 随机：数据采样随机（有放回的随机采样，60%~80%），特征选择随机（有放回的随机选择）
② 森林：多个决策树并行放在一起
思路：从数据集D中采样出T个含有m个训练集的采样集，然后基于每个采样集训练出T个基学习器，再将这些基学习器进行结合，即可得到集成学习器。在对输出进行预测时，Bagging通常对分类进行简单投票法，对回归使用简单平均法。
通过限制深度、变量个数、叶节点、样本数等条件来实现弱分类器（运行效率高；泛化能力比较强；）

随机森林 Random Forest

✓ 它能够处理很高维度（feature很多）的数据，并且不用做特征选择
✓ 训练完成后，它能够给出哪些feature比较重要（特征随机处理）
✓ 容易做成并行化方法，速度比较快
✓ 可以进行可视化展示，便于分析
✓ 随机的意义在于保证泛化能力，因此要尽量保证每棵树不一样
✓ 理论上越多的树效果会越好，但实际上基本超过一定数量就差不多上下浮动