二分+秦九韶算法 求凸点

链接: 原题
题意就是给定一个区间，[l,r],保证函数中间有凸点，求导+秦九韶算法+二分。

秦九韶算法的公式，可将多项式的计算时间复杂度降到o(n)

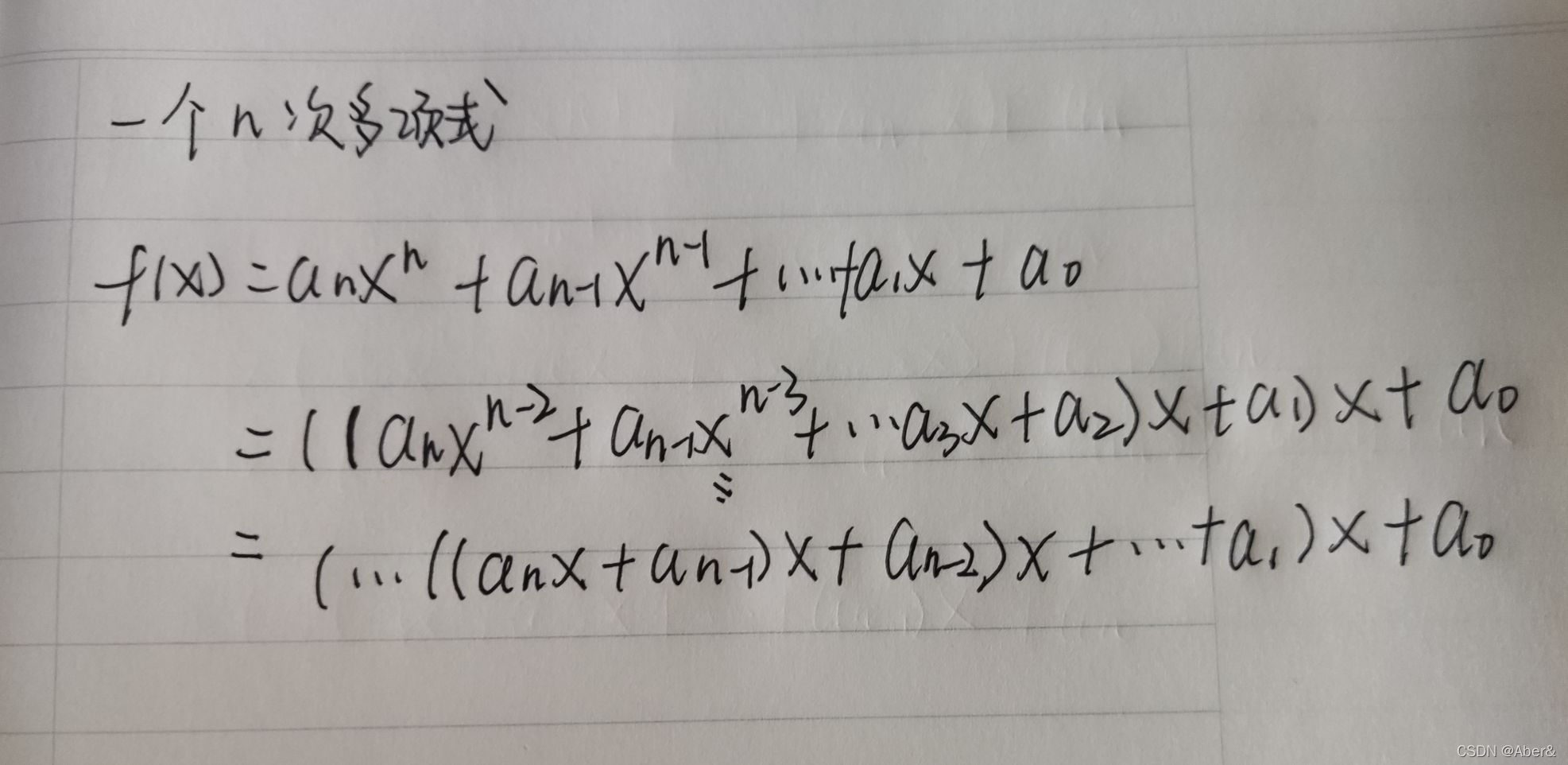
#include <bits/stdc++.h>
using namespace std;
const int N = 100;
const double eps = 1e-10;
int n;
double l, r, a[N];
//秦九韶公式的计算，每一个多项式的值都根据比自己高一次的值来进行计算
inline double f(double x) {
    double t[N];
    t[n] = a[n];
    for(int i = n - 1; i >= 0; --i) {
        t[i] = t[i + 1] * x + a[i];
    }
    return t[0];
}
//求导 等于求斜率 初中的公式
double check(double x) {
    double dx = eps;
    double dy = f(x + dx) - f(x);
    return dy / dx;
}
signed main() {
    scanf("%d%lf%lf", &n, &l, &r);
    for(int i = 0; i <= n; ++i) scanf("%lf", &a[n - i]);
    double ok;
    while(r - l > eps) {
        ok = (l + r) / 2;
        if(check(ok) > 0) l = ok;//一定是l=ok 往右走 往上爬
        else r = ok;
    }
    printf("%.5lf", ok);
    return 0;
}