DOB设计:
%% Controller & DoB design
% Setting feedback control (PD) gains
Kp=500; Kd=4;
C=tf([Kd Kp],[1]);
Cz=c2d(C,T,'matched');
Gcz=feedback(Gz*Cz,1);
% Design of a Q filter (Notice that the relative order of Gdnew(z) is 2)
w = 50*2*pi; Q1 = tf([w],[1 w]);
syms z; z =tf('z',T); alpha = exp(-w*T); QQ = ((1-alpha)/2*(z+1)/(z-alpha))^2;
Q = Q1*Q1;
Qz = c2d(Q,T,'matched')
Qz = Qz / dcgain(Qz); % To make the Q(exp(j0T)) = 1
[aQ,bQ] = tfdata(Qz,'v'); % Model parameters of Q filter
% Design of DOB
GDOB = minreal(Qz*Gz^-1);
[aD,bD] = tfdata(GDOB,'v'); % Model parameters of Q*G^-1
%% Disturbance
v = zeros(1,N);
for k=2:N, v(k) = (yd(k)-yd(k-1))/T; end
for k=1:N
g = 9.81;
gear_ratio = 1; l = 5; m = 20;
d1(k) = -m*g*l*gear_ratio*sin(yd(k)*10*pi/180); % Gravity
d2(k) = 800*(sin(2*pi*0.3*t(k))) + 500*(sin(2*pi*1.3*t(k))) + 200*(sin(2*pi*2*t(k)));
d(k) = d1(k) + d2(k);
end
%% Simulation
y(1:3) = 0; iter = 0;
for k=1:4,
switch(PAA),
case 1, var(:,k) = [b(2) b(3) a(2) a(3)]; F = eye(4)*10^10; ramda = 0.8;
end;
end
for k = 4:N,
% Simulation by G(z), i.e., actual dynamics
y(k) = -b(2)*y(k-1) -b(3)*y(k-2) +a(1)*ua(k) +a(2)*ua(k-1) +a(3)*ua(k-2);
e(k) = yd(k) - y(k);
dhat(k) = 1/(an(2)*bQ(1))*(...
(aQ(2)*bn(1)*y(k) + (aQ(3)*bn(1) + aQ(2)*bn(2))*y(k-1) + (aQ(2)*bn(3)+aQ(3)*bn(2))*y(k-2) + aQ(3)*bn(3)*y(k-3) ) +...
- ( an(2)*aQ(2)*ud(k-1) +(an(3)*aQ(2) + an(2)*aQ(3))*ud(k-2) + an(3)*aQ(3)*ud(k-3) ) +...
- ( an(3)*bQ(1) + an(2)*bQ(2) )*dhat(k-1) - (an(2)*bQ(3)+an(3)*bQ(2))*dhat(k-2) - an(3)*bQ(3)*dhat(k-3) ...
);
% Control
uc(k) = Kp*e(k) + Kd*(e(k)-e(k-1))/T; % PD control
switch(DOB_Rejection)
case 0, ud(k) = uc(k); % Disturbance rejection
case 1, ud(k) = uc(k) - dhat(k); % Disturbance rejection
end
% Saturation of control input
if ud(k) > 5000, ud(k) = 5000; end; if ud(k) < -5000, ud(k) = -5000; end
switch(PAA)
case 1,
phi(:,k) = [-y(k-1) -y(k-2) ud(k-1) ud(k-2)]'; % adaptive algorithm
F = F - (F*phi(:,k)*phi(:,k)'*F)/(1+phi(:,k)'*F*phi(:,k));
output = y(k);
theta = theta + F*phi(:,k)*(output - theta'*phi(:,k));
var(:,k) = theta;
iter = 1;
end
% Disturbance (it is unknown in practice)
ua(k) = ud(k) + d(k); % Actual input with a disturbance. The control algorithm has no information on d(k)
end
仿真结果:
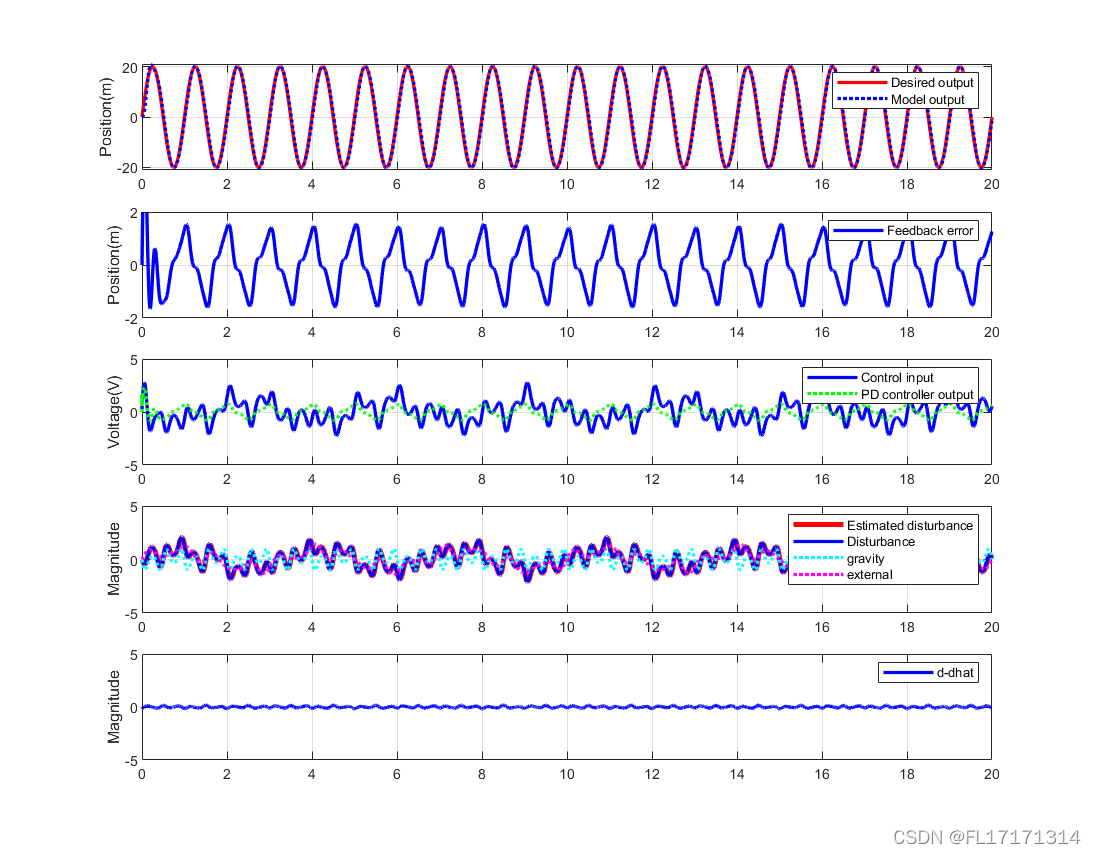




 本文介绍了DOB(Delay-Optimized Buffering)算法的设计思路,并提供了具体的仿真结果展示,通过实例解析DOB如何在实际场景中优化性能。
本文介绍了DOB(Delay-Optimized Buffering)算法的设计思路,并提供了具体的仿真结果展示,通过实例解析DOB如何在实际场景中优化性能。
















 530
530

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








