数学建模：现代优化算法之粒子群算法

数学建模：现代优化算法之粒子群算法

《数学建模算法与应用》在现代优化算法中没有提及，依照组内进度要求，所以需要在此节补充有关“粒子群算法”的内容。

---

---

前言

先来看一段视频：Matlab 粒子群算法PSO实例学习（有代码和详细注释）

来自 “百科”： 粒子群优化算法(Particle Swarm optimization,PSO)又翻译为粒子群算法、微粒群算法、或微粒群优化算法。是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法。通常认为它是群集智能 (Swarm intelligence, SI) 的一种。它可以被纳入多主体优化系统(Multiagent Optimization System, MAOS)。粒子群优化算法是由Eberhart博士和kennedy博士发明。

---

一、算法简介

参考优快云博主「lx青萍之末」的原创文章
最优化算法之粒子群算法（PSO）

二、算法步骤

1.初始化

PSO初始化为一群随机粒子(随机解)，然后通过迭代找到最优解，在每一次迭代中，粒子通过跟踪两个“极值”来更新自己。第一个就是粒子本身所找到的最优解，这个解叫做个体极值pBest，另一个极值是整个种群找到的最优解，这个极值是全局极值gBest。另外也可以不用整个种群而只是用其中一部分最优粒子的邻居，那么在所有邻居中的极值就是局部极值。

2.更新规则

公式(1)的第一部分称为【记忆项】，表示上次速度大小和方向的影响；公式(1)的第二部分称为【自身认知项】，是从当前点指向粒子自身最好点的一个矢量，表示粒子的动作来源于自己经验的部分；公式(1)的第三部分称为【群体认知项】，是一个从当前点指向种群最好点的矢量，反映了粒子间的协同合作和知识共享。粒子就是通过自己的经验和同伴中最好的经验来决定下一步的运动。以上面两个公式为基础，形成了PSO的标准形式。

三、PSO算法的流程图和伪代码

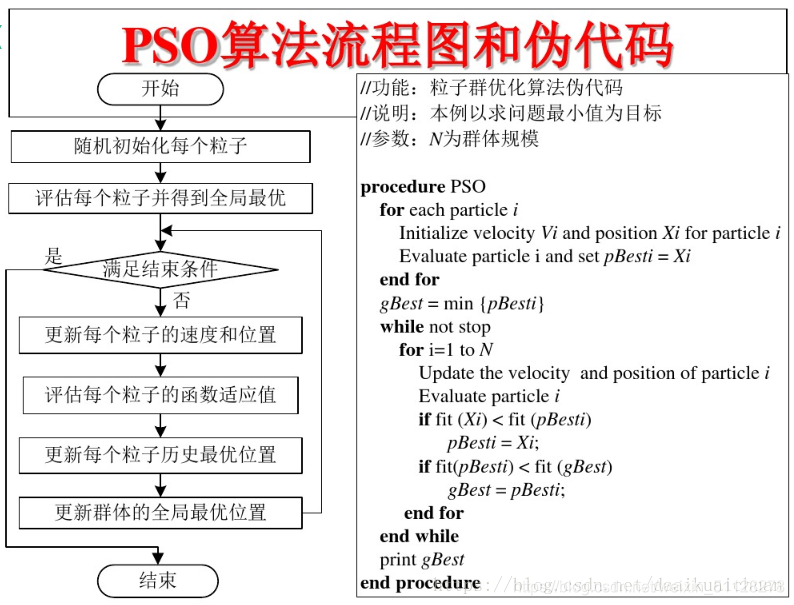
四、PSO算法举例

【例一】

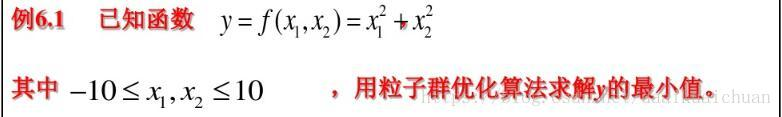
【解】

【例二】 本部分参考优快云博主「nightmare_dimple」的原创文章
原文链接：https://blog.youkuaiyun.com/nightmare_dimple/article/details/74331679

对于函数 f=xsin(x)cos(2x)-2xsin(3x) ，求其在区间[0,20]上该函数的最大值。
【解】

clc;clear;close all;
%% 初始化种群
f= @(x)x .* sin(x) .* cos(2 * x) - 2 * x .* sin(3 * x); % 函数表达式
figure(1);ezplot(f,[0,0.01,20]);
N = 50;                         % 初始种群个数
d = 1;                          % 空间维数
ger = 100;                      % 最大迭代次数     
limit = [0, 20];                % 设置位置参数限制
vlimit = [-1, 1];               % 设置速度限制
w = 0.8;                        % 惯性权重
c1 = 0.5;                       % 自我学习因子
c2 = 0.5;                       % 群体学习因子 
for i = 1:d
    x = limit(i, 1) + (limit(i, 2) - limit(i, 1)) * rand(N, d);%初始种群的位置
end
v = rand(N, d);                  % 初始种群的速度
xm = x;                          % 每个个体的历史最佳位置
ym = zeros(1, d);                % 种群的历史最佳位置
fxm = zeros(N, 1);               % 每个个体的历史最佳适应度
fym = -inf;                      % 种群历史最佳适应度
hold on
plot(xm, f(xm), 'ro');title('初始状态图');
figure(2)
%% 群体更新
iter = 1;
record = zeros(ger, 1);          % 记录器
while iter <= ger
     fx = f(x) ; % 个体当前适应度   
     for i = 1:N      
        if fxm(i) < fx(i)
            fxm(i) = fx(i);     % 更新个体历史最佳适应度
            xm(i,:) = x(i,:);   % 更新个体历史最佳位置
        end 
     end
if fym < max(fxm)
        [fym, nmax] = max(fxm);   % 更新群体历史最佳适应度
        ym = xm(nmax, :);      % 更新群体历史最佳位置
 end
    v = v * w + c1 * rand * (xm - x) + c2 * rand * (repmat(ym, N, 1) - x);% 速度更新
    % 边界速度处理
    v(v > vlimit(2)) = vlimit(2);
    v(v < vlimit(1)) = vlimit(1);
    x = x + v;% 位置更新
    % 边界位置处理
    x(x > limit(2)) = limit(2);
    x(x < limit(1)) = limit(1);
    record(iter) = fym;%最大值记录
%     x0 = 0 : 0.01 : 20;
%     plot(x0, f(x0), 'b-', x, f(x), 'ro');title('状态位置变化')
%     pause(0.1)
    iter = iter+1;
end
figure(3);plot(record);title('收敛过程')
x0 = 0 : 0.01 : 20;
figure(4);plot(x0, f(x0), 'b-', x, f(x), 'ro');title('最终状态位置')
disp(['最大值：',num2str(fym)]);
disp(['变量取值：',num2str(ym)]);

结果如下：

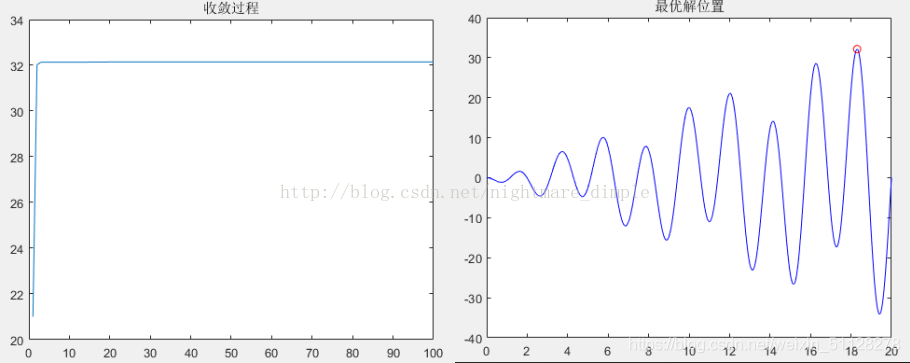
由上图可以看出算法已成功找出了最优解，其最优解为18.3014，而其最大值为32.1462。
如果想看粒子群算法中粒子的搜索过程的可以将代码中注释掉的三行代码放上去。效果是这样的：

【例三】
版权声明：本部分参考优快云博主「箫韵」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.youkuaiyun.com/qq_41053605/article/details/88924287

（1）构建目标函数。这里使用只有两个参数的函数，这样便于画出三维图型。

function y=A11_01(x)
y=x(1)^2+x(2)^2-x(1)*x(2)-10*x(1)-4*x(2)+60;

首先从直观上看看这个函数：

x1=-15:1:15;
x2=-15:1:15;
[x1,x2]=meshgrid(x1,x2);
y=x1.^2+x2.^2-x1.*x2-10.*x1-4.*x2+60;
mesh(x1,x2,y);

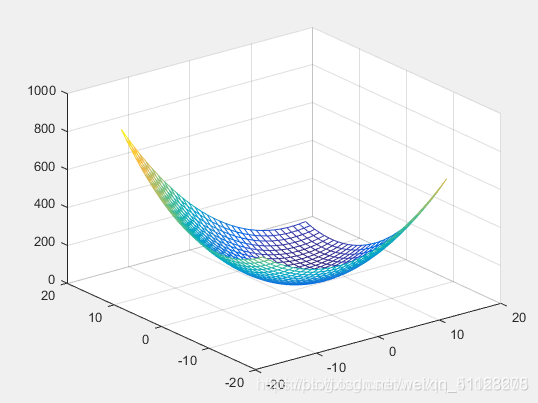
图 1 目标函数的三维网格图

（2）整体实现代码

clear 
clc

%绘制原图        图1目标函数的三维网格图
x1=-15:1:15;
x2=-15:1:15;
[x1,x2]=meshgrid(x1,x2);
y=x1.^2+x2.^2-x1.*x2-10.*x1-4.*x2+60;
mesh(x1,x2,y);    
hold on;

%%预设参数
n=100; %粒子群的规模
d=2; %变量个数
c1=2;
c2=2;
w=0.9;%权重一般设为0.9
K=50; %迭代次数

%%分布粒子的取值范围及速度的取值范围
x=-10+20*rand(n,d);  %x在[-10,10]中取值
v=-5+10*rand(n,d); %v在[-5,5]中取值

%%计算适应度
fit=zeros(n,1);
for j=1:n
    fit(j)=A11_01(x(j,:));
end
pbest=x;
ind=find(min(fit)==fit);
gbest=x(ind,:);
h=scatter3(x(:,1),x(:,2),fit,'o');  %图2 粒子的初始分布图

%%更新速度与位置
for i=1:K
    for m=1:n
       v(m,:)=w*v(m,:) + c1*rand*(pbest(m,:)-x(m,:)) + c2*rand*(gbest-x(m,:));%rand是[0,1]随机数
       
       v(m,find(v(m,:)<-5))=-5;%这里发现速度小于-5时取-5
       v(m,find(v(m,:)>5))=5;%这里发现速度大于5时取5
       
       x(m,:)=x(m,:)+0.5*v(m,:);
       x(m,find(x(m,:)<-10))=-10;%这里发现位置小于-10时取-10
       x(m,find(x(m,:)>10))=10;%这里发现位置大于10时取10
       
       %重新计算适应度
       fit(m)=A11_01(x(m,:));
       if x(m,:)<A11_01(pbest(m,:))
           pbest(m,:)=x(m,:);
       end
       if A11_01(pbest(m,:))<A11_01(gbest)
           gbest=pbest(m,:);
       end
    end
    fitnessbest(i)=A11_01(gbest);
    pause(0.01);    %为了直观，每更新一次，暂停0.01秒
    h.XData=x(:,1);
    h.YData=x(:,2);
    h.ZData=fit;
end
% hold off;
% plot(fitnessbest);
% xlabel('迭代次数');

（3）粒子的初始分布图

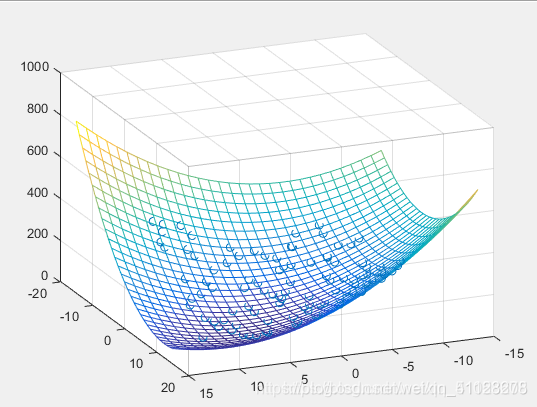
图2 粒子的初始分布图

（4）粒子群移动图

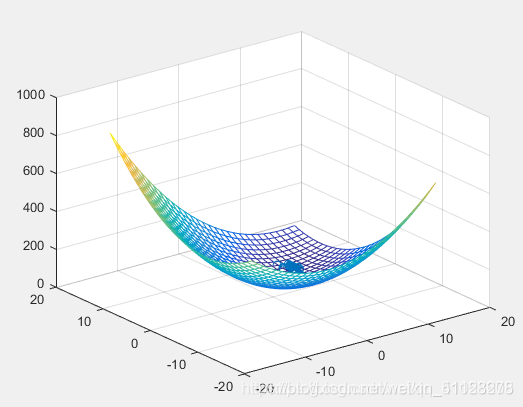
图 3 粒子群移动图

（5）迭代过程

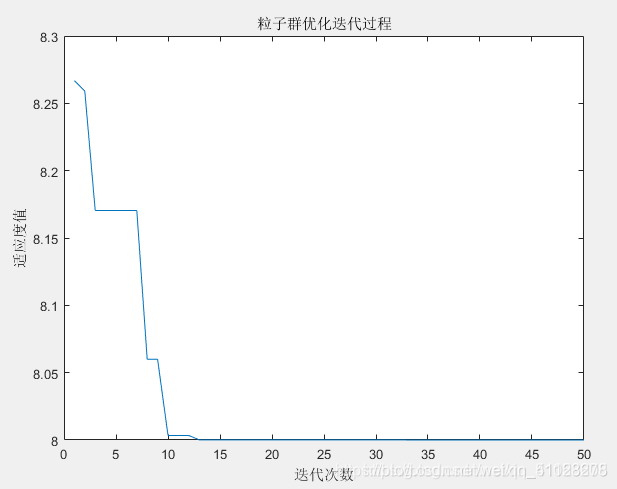
图 4 迭代过程图
从图中可以看出，迭代次数基本上在13,14的时候就达到最优，即目标函数取得最小值为8.

五、PSO算法的demo

#include <iostream>
#include <vector>
#include <cmath>
#include <map>
#include <algorithm>
#include <random>
#include <ctime>
#include <Eigen/Dense>
using namespace Eigen;
using namespace std;

const int dim = 1;//维数
const int p_num = 10;//粒子数量
const int iters = 100;//迭代次数
const int inf = 999999;//极大值
const double pi = 3.1415;
//定义粒子的位置和速度的范围
const double v_max = 4;
const double v_min = -2;
const double pos_max = 2;
const double pos_min = -1;
//定义位置向量和速度向量
vector<double> pos;
vector<double> spd;
//定义粒子的历史最优位置和全局最优位置
vector<double> p_best;
double g_best;
//使用eigen库定义函数值矩阵和位置矩阵
Matrix<double, iters, p_num> f_test;
Matrix<double, iters, p_num> pos_mat;

//定义适应度函数
double fun_test(double x)
{
    double res = x * x + 1;
    return res;
}

//初始化粒子群的位置和速度
void init()
{
    //矩阵中所有元素初始化为极大值
    f_test.fill(inf);
    pos_mat.fill(inf);
    //生成范围随机数
    static std::mt19937 rng;
    static std::uniform_real_distribution<double> distribution1(-1, 2);
    static std::uniform_real_distribution<double> distribution2(-2, 4);
    for (int i = 0; i < p_num; ++i)
    {
        pos.push_back(distribution1(rng));
        spd.push_back(distribution2(rng));
    }
    vector<double> vec;
    for (int i = 0; i < p_num; ++i)
    {
        auto temp = fun_test(pos[i]);//计算函数值
        //初始化函数值矩阵和位置矩阵
        f_test(0, i) = temp;
        pos_mat(0, i) = pos[i];
        p_best.push_back(pos[i]);//初始化粒子的历史最优位置
    }
    std::ptrdiff_t minRow, minCol;
    f_test.row(0).minCoeff(&minRow, &minCol);//返回函数值矩阵第一行中极小值对应的位置
    g_best = pos_mat(minRow, minCol);//初始化全局最优位置
}

void PSO()
{
    static std::mt19937 rng;
    static std::uniform_real_distribution<double> distribution(0, 1);
    for (int step = 1; step < iters; ++step)
    {
        for (int i = 0; i < p_num; ++i)
        {
            //更新速度向量和位置向量
            spd[i] = 0.5 * spd[i] + 2 * distribution(rng) * (p_best[i] - pos[i]) +
                2 * distribution(rng) * (g_best - pos[i]);
            pos[i] = pos[i] + spd[i];
            //如果越界则取边界值
            if (spd[i] < -2 || spd[i] > 4)
                spd[i] = 4;
            if (pos[i] < -1 || pos[i] > 2)
                pos[i] = -1;
            //更新位置矩阵
            pos_mat(step, i) = pos[i];
        }
        //更新函数值矩阵
        for (int i = 0; i < p_num; ++i)
        {
            auto temp = fun_test(pos[i]);
            f_test(step, i) = temp;
        }
        for (int i = 0; i < p_num; ++i)
        {
            MatrixXd temp_test;
            temp_test = f_test.col(i);//取函数值矩阵的每一列
            std::ptrdiff_t minRow, minCol;
            temp_test.minCoeff(&minRow, &minCol);//获取每一列的极小值对应的位置
            p_best[i] = pos_mat(minRow, i);//获取每一列的极小值，即每个粒子的历史最优位置
        }
        g_best = *min_element(p_best.begin(), p_best.end());//获取全局最优位置
    }
    cout << fun_test(g_best);
}

int main()
{
    init();
    PSO();
    system("pause");
    return 0;
}

总结

参考内容：

版权声明：本文部分为优快云博主「lx青萍之末」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.youkuaiyun.com/daaikuaichuan/article/details/81382794

————————————————
版权声明：本文部分为优快云博主「nightmare_dimple」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.youkuaiyun.com/nightmare_dimple/article/details/74331679