探秘XGBoost：GBDT算法的升级版极端梯度提升树解析

不一样的邓先生

已于 2024-02-26 21:43:25 修改

阅读量1k

点赞数 14

文章标签：机器学习算法人工智能

于 2024-02-26 21:17:44 首次发布

本文链接：https://blog.youkuaiyun.com/weixin_50249953/article/details/136297288

版权

在上一篇文章中，以及给大家讲解了提升算法的理论知识以及GBDT提升树相关的理论知识，并用实际案例给大家展示了GBDT算法实际运行流程，今天，我们给大家分享的是XGBoost(极端梯度提升树)相关的理论知识，XGBoost算法是对GBDT算法的改进，同时在实际工作之中的性能也是比GBDT算法性能要好的，因此，在实际应用过程中，我们对XGBoost算法使用更多，所以我们必须得了解XGBoot算法的理论知识，从理论层面深入了解XGBoost算法，有助于我们实际过程中的应用，当然XGBoost是对GBDT算法的改进，因此，前面梯度提升算法以及梯度提升树算法相关的思想有助于我们理解XGBoost算法，如果大家需要了解的，请查看上一篇文章，“明天科技屋”公众号获取更方便。

XGBoost是梯度提升树GBDT算法的改进，因此XGBoost算法也是基于Cart树为集学习器的boosting集成模型。XGBoost的所有模型都是决策树模型，从初始化的模型就是决策树模型，我们在上一篇文章中提到过GBDT，大家记得GBDT的初始化模型是什么吗？是一个使得与所有真实值残差平方和最小的常数，XGBoost是多个决策树模型的集成，初始化的模型就是决策树模型，这是XGBoost模型和GBDT模型在模型上的一点小差别，XGBoost模型如下：

$F_{k-1}(x_{i})$ 代表前k-1个决策树模型的累加和， ${f_{k}}(x_{i})$ 代表第k个决策树模型，即XGBoost模型就是k个决策树模型的累加和。在训练模型之前，首先应该有一个目标函数，XGBoost算法的目标函数是:

主要由两部分组成，前面的一部分是损失函数，及真实值与预测值的残差平方和，后面的一部分为正则项，用来控制模型的复杂度，防止出现过拟合，其具体表达式为：

该表达式主要有两部分组成， $\gamma T$ 代表模型的叶子结点与及其控制系数，大家应该很容易能够理解这部分对模型复杂度的影响，当一个模型叶子结点越多的时候，该模型划分得越细，因此会增加模型的复杂度，大家其实不好理解的是第二部分，第二部分是L2正则项，这一部分值越大的话，模型复杂度就越高， $\omega$ 在XGBoost算法中代表叶子结点的预测值，并且该预测值代表了每个叶子结点的权重，对于这一块知识，我在网上寻找了很久的答案，看到一个最能理解的答案就是当一个模型的预测值越大的时候，真实值与预测值之间的残差就越小，那么后面的模型都是基于残差的学习，因此，后面的模型能够学习到的残差就越小，其他模型对预测值的影响就会降低，你可能会讲，那第一个模型学习到很多，其他模型学习得很少，不是最终也是在往真实值靠近吗？我就是想要这种效果，但是实际上，当一个模型的预测值越大（权重），模型都是基于训练数据进行的训练，模型可能学习到了训练数据中某些异常值的影响，当这种影响不是很大的时候，模型性能可能会非常非常好，但是当影响比较大的时候，模型更可能倾向于过拟合，整个模型受到那个模型的影响比较大，当未知数据出现时，模型的性能可能会非常差，同时由于那一个模型占据了太大的预测，其他模型也无法对该模型进行调整，我们希望的是每个模型尽可能保持小的权重，不会对整个模型产生太大影响，通过多个模型组合能够实现对目标的预测，因此正则化项确保了叶子结点的权重尽可能小。

对于这个公式我相信大家应该能够理解， $\hat{y_{i}^{s}} = \hat{y_{i}^{s-1}}+f(x_{i})$ ，后面需要使用，第s轮模型等于第s-1轮模型加上新的子模型，在该式子中，当我们产生新模型的时候，前s-1轮训练的模型是已知的，大家可以当作一个常数看待。

在上面我们的目标函数公式中，我们对其进行了改写：

大家可以看到，就是将第s轮模型拆分成了前s-1轮模型与新模型的和，同时对于上面的求和正则化项 $\sum \Omega (f_{k}) = \sum_{1}^{s-1}\Omega (f_{k})+\Omega (f_{s})$ ，其中 $\sum_{1}^{s-1}\Omega (f_{k})$ 是前s-1个模型的正则化项也是一个常数，所以不会影响到模型目标的求解，因此，可以直接去掉。

在XGBoost中，使用的泰勒公式来近似目标函数的求解，大家如果泰勒公式不太清楚的请直接去网上查询，因此，我们使用泰勒公式对目标函数进行变换，得到，这一块太难写上来了，真诚希望大家能够理解：

其中， $g_{i}$ 为真实值与前s-1模型预测值的损失函数的一阶导， $h_{i}$ 代表真实值与前s-1次模型预测值的二阶导数：

在上面的目标函数公式中，真实值与s-1轮模型的预测值都是知道的，因此，是一个常数，不影响目标函数求解，同时将第s个模型的正则化项带入目标函数中，化简结果得：

大家可以在该模型中可以看见前半部分损失函数的部分是对样本的累加和得到，从i=1到i=n个样本，后面的L2正则化项是采用叶子结点数量来进行的累加和，从j=1到j=T个叶子结点计算累加得到，不统一不利于化简，同时由于每个样本通过模型都会被划分到一个叶子结点上，因此我们可以从叶子结点的角度出发来计算样本的损失函数部分，因此，公式转换成了：

$w_{j}$ 代表第j个叶子结点的输出值， $I_{j}$ 代表第j个叶子结点区域，因此该式子从叶子结点角度出发，如果某个样本是属于第j个叶子结点区域，那么对应的输出值就是 $w_{j}$ ，将每个叶子结点中包含的样本涉及到的损失求和就行，文字彰显有限，希望大家能够理解，进行了这样的转换之后，大家可以明显感觉到模型发生了巨变，答案正在向你靠近吗？没错在上是中 $g_{i}$ 和 $h_{i}$ 都是真实值与s-1轮模型残差平方和到一阶和二阶导数，是个常数， $\lambda$ 也是一个我们设置的常数，从而我们的目标函数可以看作是一个自变量为 $w_{j}$ 、因变量为obj的一元二次函数，从而可以求解叶子结点j的最优 $w_{j}$ 得：

从结果可以看出，叶子权重不仅受到了一阶、二阶偏导数影响，还收到了L2正则化系数的影响，当正则化系数越大的时候，叶子权重结点越小，因此，正则化系数起到了防止过拟合的作用。在得到了叶子阶段的最优输出值 $w_{j}^{*}$ 之后，将 $w_{j}^{*}$ 带入目标函数中得到最优的目标函数为：

为了简化表达式，我们将使用变量替代 $G_{j}$ 表示 $\sum g_{i}$ ，用 $H_{j}$ 表示 $\sum h_{i}$ ，则有

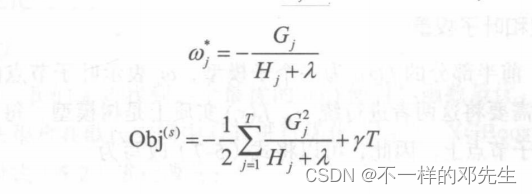
在得出该公式之后，在每一轮训练中，我们使用该公式可以得出每一轮训练候选模型的得分，只要选择得分最低的模型作为该轮训练模型的最优模型即可，由于我们得出最优的叶子结点权重以及叶子结点个数之后，我们是可以确定决策树的模型的，但是这样的模型并不是唯一的，因为输出为指定值以及指定个数的决策树模型肯定会存在多个，同时由于叶子结点的个数也是可以拓展的，因此，按照这样的方式来备选的决策树模型有无穷多个，因此，遍历选择最优的方法不具备实操性。

XGBoost算法采取的是贪心算法来进行树的构建，即先从根结点开始，计算结点分裂之后比结点分裂之前的目标函数值是否减少，如果减少，就分裂，如果不减少，就不分裂，假设当前分裂结点为j,没有分裂之前只有一个结点，树的复杂度贡献为 $\gamma$ ,则其对目标函数的贡献为

分裂之后，两个子结点对目标函数的共享为：

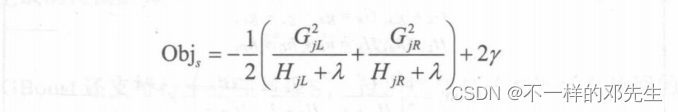
前后得到的目标函数变化为：

最终得到结点的可分裂目标函数为：

其中，G和H表示当前结点的一阶、二阶梯度统计和; $G_{L}$ 和 $G_{R}$ 分别表示由当前结点分裂出的左子结点和右子结点样本集的一阶梯度统计和； $H_{L}$ 和 $H_{R}$ 分别代表当前结点分裂出的左子结点和右子结点样本集的二阶梯度统计和。在一个叶子结点分裂过程中，选取贡献差最大的特征及其切分点作为最优特征及其最优切分点，使叶子结点按照最优特征和最优切分点进行分裂。经过以上过程，生成了一轮训练中的最优决策树，在训练完之后，XGBoost会对其进行剪枝，判断当前结点的收益是否小于定义的收益，如果小于，则进行剪枝。剪完之后将新模型加入当前模型之中，模型如下：