C++_022栈的基本使用

最新推荐文章于 2025-04-28 15:01:16 发布

一道秘制的小菜

最新推荐文章于 2025-04-28 15:01:16 发布

阅读量1k

点赞数 11

分类专栏：深入浅出C++ 文章标签： c++ 开发语言算法 vim 学习

本文链接：https://blog.youkuaiyun.com/weixin_47702917/article/details/143274137

版权

深入浅出C++ 专栏收录该内容

12 篇文章

订阅专栏

一、栈的定义

1. stack是一种容器适配器，专门用在具有后进先出的操作的上下文当中，其删除只能从容器的一端进行元素的插入与提取操作；

2. stack与deque都没有迭代器！因为不能任意的访问容器，只能从在规定下访问；

接下来我们尝试测试一下：

int main()
{
	stack<int> st1;
	st1.push(1);
	st1.push(2);
	st1.push(3);
	st1.push(4);
	// 遍历容器中的数据
	while (!st1.empty())
	{
		cout << st1.top() << " ";
		st1.pop();
	}
	cout << endl;
	return 0;
}

这里我们遍历不能使用迭代器，因此while的判断条件为 !st1.empty() ，依次出数据，当stack为空则停止；

接下来我们测试queue：

	queue<int> de1;
	de1.push(1);
	de1.push(2);
	de1.push(3);
	de1.push(4);
	// 遍历容器中的数据
	while (!de1.empty())
	{
		cout << de1.front() << " ";
		de1.pop();
	}
	cout << endl;

队列的遍历方法与stack的一样，但是有一点不同的是：stack是取栈顶元素top，但是队列是取头部元素front；

练习题1：最小栈

. - 力扣（LeetCode）

在这里，我们首先的思路是：

设置两个成员变量，一个是stack，一个是min最小值；

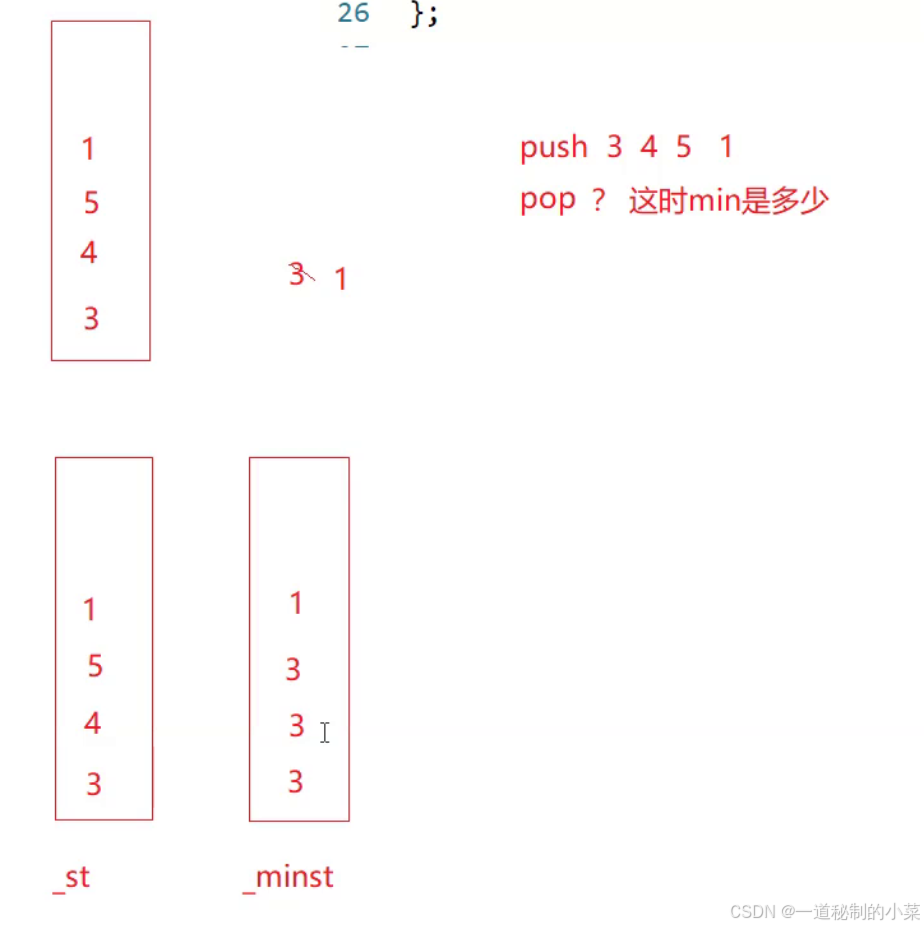
但是可能会发生下面这种情况：如果我们依次插入的数据时3 4 5 1；

对应的最小值最初为3，当1出现的时候变为1，但是如果我们此时把1给pop掉，那么怎么获得之前得到的3呢？

重新遍历的话无法满足时间复杂度为常数；

解决方法：

我们可以设置两个栈，如上图所是，一个用于普通的数据记录，一个用于记录stack的最小值；

当左边的stack进行pop操作的时候，右边的最小栈也进行pop！getmin的数据直接从最小栈中获取！

接下来我们可以进行再优化：

当_st的数据和_minst的数据相等时再pop！

并且如果push的值和最小值相等，此时最小栈中也要进行push！

示例代码如下所示：

class MinStack {
public:
    MinStack() 
    {}
    
    void push(int val) {
    _st.push(val);
    // 判断最小栈是否需要插入
    if(_minst.empty() || val <= _minst.top())
    {
        _minst.push(val);
    }

    }
    void pop() {
    // 先判断最小栈是否需要删除
    if(_st.top() == _minst.top())
        {
            _minst.pop();
        }
    _st.pop();
    }
    int top() {
        return _st.top();
    }
    int getMin() {
     return _minst.top();   
    }
private:
    stack<int> _st;
    stack<int> _minst;
};

第二题：栈的弹出压入序列

栈的压入、弹出序列_牛客题霸_牛客网

解：这道题时输入一个栈的压入序列，判断弹出序列是否满足规则，如果不满足返回false；

定义一个空栈来检测是否满足顺序！

class Solution {
public:
    bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {
        // 输入一个入栈的顺序，输出一个出栈的顺序
        // 判断是否满足出栈的顺序
        stack<int> st1;
        int pushi = 0;
        int popi = 0;
        while(pushi < pushV.size())
        {
            // 空栈先进数据
            st1.push(pushV[pushi]);
            pushi++;
            // 判断插入的数据与出栈数据是否匹配
            if(st1.top() != popV[popi])
            {
               // 不匹配 --- 插入数据
               continue; 
            }
            else
            {
                // 匹配 --- 出数据
                while(!st1.empty() && st1.top() == popV[popi])
                {
                    st1.pop();
                    ++popi;
                }
            }
            
        }
        return st1.empty();

    }
};

首先我们先插入数据，然后判断插入的数据和对应的出栈的数据是否相等，如果相等就进行pop；如果不相等再进行push；

第三题：求解逆波兰表达式

. - 力扣（LeetCode）

这里我们需要科普两个知识点：

逆波兰表达式就是后缀表达式！

解题思路：

逆波兰表达式比较适合使用栈来进行运算：

遇到操作数进行入栈；
遇到操作符，将栈顶的两个元素取出进行运算，运算结果继续入栈；
且先取出来的元素是右操作数（符合栈的规则）；
最后剩下的一个元素即是所求的值；

根据上面的步骤我们可以得到代码：

class Solution {
public:
    int evalRPN(vector<string>& tokens) {
        stack<int> s;
        // 遍历tokens
        for(auto& str:tokens)
        {
            if(str == "+" || str == "-" || str == "*" || str == "/")
            {
                // 取出两个栈顶元素进行运算
                // 再将结果进行入栈
                int right = s.top();
                s.pop();
                int left = s.top();
                s.pop();
                // switch只能是整数 --- 这里char类型可以和int类型互通
                switch(str[0])
                {
                    case '+':
                    s.push(left+right);
                    break;
                }
                switch(str[0])
                {
                    case '-':
                    s.push(left-right);
                    break;
                }                
                switch(str[0])
                {
                    case '*':
                    s.push(left*right);
                    break;
                }
                switch(str[0])
                {
                    case '/':
                    s.push(left/right);
                    break;
                }                
            }
            else{
                // 此时元素为数字
                s.push(stoi(str));
            }
        }
        return s.top();
    }
};

科普点：

运算符的比较不是从全局的运算符进行比较，而是相邻之间的运算符比较！

例如这里3*4虽然*的运算级最高，但是不影响进行+

即中缀表达式转化为后缀表达式如下所示（不带括号的情况下）：

遇到括号可以考虑使用递归 / 优先级来解决

栈的模拟实现

注意点：分析下面两种情况

其中，stack.h中包含了<vector>和<list>两个头文件；

结果是第一个无法编译成功，第二个可以编译成功！

这是因为编译器编译是从上往下的，分析第一种情况：当include<Stack.h>文件的时候，里面的命令空间中有vector和list的使用，使用这些头文件必须要展开std！但是由于向上编译中没有发现展开，因此报错！

栈的实现可以使用数组/链表，两种都可以！

并且由于栈底层采用空间适配器用数组或链表来实现，因此栈不需要自己写构造/拷贝构造/析构等函数，因为底层会自动调用数组 / 链表的函数！

对于队列queue来说：

std库里面是有基于链表实现的，但是没有基于数组实现，这是因为对于pop来说，如果是用顺序表，效率非常底下（顺序表的头删效率非常低）！

这里我们给出模拟的queue和stack的代码：

对于Stack.h文件如下：

#pragma once
#include<vector>
#include<list>

namespace shyd {
template<class T,class Container = list<T>>
class deque
{
public:
	void push(const T& x)
	{
		_con.push_back(x);
	}
	void pop()
	{
		//_con.pop_front();
		_con.erase(_con.begin());
	}
	T& front()
	{
		return _con.front();
	}
	size_t size()
	{
		return _con.size();
	}
	bool empty()
	{
		return _con.empty();
	}
private:
	Container _con;
};
// 测试案例for deque
void test_deque()
{
	// deque base on 数组(效率底下，不建议使用)
	deque<int,vector<int>> de1;
	de1.push(1);
	de1.push(2);
	de1.push(3);
	de1.push(4);
	while (!de1.empty())
	{
		cout << de1.front() << " ";
		de1.pop();
	}
	cout << endl;
	// deuqe base on链表
	deque<int, list<int>> de2;
	de2.push(1);
	de2.push(2);
	de2.push(3);
	de2.push(4);
	while (!de2.empty())
	{
		cout << de2.front() << " ";
		de2.pop();
	}
	cout << endl;
}
}

Queue.h文件如下：

#pragma once
#include<vector>
#include<list>

namespace shyd {
template<class T,class Container = list<T>>
class deque
{
public:
	void push(const T& x)
	{
		_con.push_back(x);
	}
	void pop()
	{
		//_con.pop_front();
		_con.erase(_con.begin());
	}
	T& front()
	{
		return _con.front();
	}
	size_t size()
	{
		return _con.size();
	}
	bool empty()
	{
		return _con.empty();
	}
private:
	Container _con;
};
// 测试案例for deque
void test_deque()
{
	// deque base on 数组(效率底下，不建议使用)
	deque<int,vector<int>> de1;
	de1.push(1);
	de1.push(2);
	de1.push(3);
	de1.push(4);
	while (!de1.empty())
	{
		cout << de1.front() << " ";
		de1.pop();
	}
	cout << endl;
	// deuqe base on链表
	deque<int, list<int>> de2;
	de2.push(1);
	de2.push(2);
	de2.push(3);
	de2.push(4);
	while (!de2.empty())
	{
		cout << de2.front() << " ";
		de2.pop();
	}
	cout << endl;
}
}

然后给出简单的test.cpp

#define  _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
using namespace std;
#include"stack.h"
#include"Deque.h"
int main()
{
	//shy::test_stack();
	shyd::test_deque();

	return 0;
}

虽然使用数组和链表可以模拟实现stack和queue，但是std的官方使用的是deque作为适配器，接下来我们了解下deque文件：

参考链接如下所示：https://cplusplus.com/reference/deque/deque/?kw=deque

双端队列（通常发音为“deck” ）是双端队列的不规则缩写。双端队列是具有动态大小的序列容器，可以在两端（前端或后端）扩展或收缩。特定库可能以不同的方式实现双端队列，通常是某种形式的动态数组。

可以看到，这个容器的接口非常丰富，几乎集合了数组和链表两者的优点。但是deque的效率不高。

接下来我们测试一组数据，分别使用deque直接进行排序和将deque拷贝到vector，使用vector排序，然后再将数据拷贝到deque当中，测试函数如下所示：

void test_op()
{
	srand(time(0));
	// 设置数据
	const int N = 1000000;
	vector<int> v1;
	vector<int> v2;
	//扩容
	v1.reserve(N);
	v2.reserve(N);

	deque<int> dq1;
	deque<int> dq2;

	//对deque插入数据
	for (int i = 0; i < N; ++i)
	{
		auto e = rand();
		dq1.push_back(e);
		dq2.push_back(e);
	}
	// 拷贝到vector排序，排完以后再拷贝回来
	int begin1 = clock();
	// 将dq1的数据先拷贝到vector
	for (auto e : dq1)
	{
		v1.push_back(e);
	}

	// 排序
	sort(v1.begin(), v1.end());

	// 拷贝回去
	size_t i = 0;
	for (auto& e : dq1)
	{
		e = v1[i++];
	}

	int end1 = clock();

	int begin2 = clock();
	//sort(v2.begin(), v2.end());
	sort(dq2.begin(), dq2.end());

	int end2 = clock();
	printf("deque copy vector sort:%d\n", end1 - begin1);
	printf("deque sort:%d\n", end2 - begin2);
}

结果如下所示：