KMP算法代码及图文方式详解

KMP算法中的next数组

KMP算法是经典的字符串模式匹配算法,比如主串str = “goodinitialize”,模式(子)串s = “init”。需要找到模式串s 在主串str中的位置。

相比暴力解法的时间复杂度为O( n×m )，其中n为主串长度，m为模式串长度，KMP算法可将时间复杂度降为O( n+m )

KMP算法，需要求解模式串的next数组，在字符串模式匹配的过程中，当模式串不匹配时，不进行回溯，而是根据已经得到的部分匹配结果，将模式串尽可能向右滑动，继续比较

注:以 1 作为模式串下标起始以及next数组起始下标，next[0]不存储数据，规定next[ 1 ] = 0

---

 前后缀以及真前后缀的概念

前缀：符号串左部的任意子串（或者说是字符串的任意首部，可包含本身）

真前缀（又称前缀真子串）：是指不包含本身的前缀

后缀：符号串右部的任意子串（或者说是字符串的任意尾部，可包含本身）

真后缀：是指不包含本身的后缀

举个例子：字符串"initialize"

所有前缀： i   in   ini   init   initi   initia   initial   initaili   initializ   initialize

所有后缀：e  ze  ize  lize  alize  ialize  tialize  itialize  nitialize  initialize

所有真前缀：i   in   ini   init   initi   initia   initial   initaili   initializ

所有真后缀：z  iz   liz   aliz   ializ   tializ   itializ   nitializ   initializ

注：单个字符存在前后缀，就是其本身，但不存在真前后缀

---

引入next数组求解方式

规定next[ 1 ] = 0

当第 i 个位置，其真前后缀部分，不存在相同的真前后缀，则next[ i ] = 1

当第 i 个位置，其真前后缀部分，存在相同的最长真前后缀，且长度位 m 时，next[ i ] = m + 1

 

通过真前后缀方式，快速求解模式串next数组过程，以模式串aabaaab为例

  ①规定：next[ 1 ]  = 0

 

 ② 字符aa，其真前后缀(字符串a)，不存在真前后缀相等的情况，next[ 2 ] = 1

  ③ 字符aab，其真前后缀(字符串aa)，存在相同最长真前缀a与最长真后缀a，字符串长度为1，next[ 3 ] = 1 + 1 = 2

 

 ④ 字符串aaba，其真前后缀(字符串aab)，不存在真前后缀相等的情况，next[ 4 ] = 1

  ⑤ 字符串aabaa，其真前后缀(字符串aaba)，存在相同的最长真前缀a与最长真后缀a，字符串长度为1，next[ 5 ] = 1 + 1 = 2

 

 ⑥ 字符串aabaaa，其真前后缀(字符串aabaa)，存在相同的最长真前缀aa与最长真后缀aa，字符串长度位2，next[ 6 ] = 1 + 2 = 3

 

 ⑦ 字符串aabaaab，其真前后缀(字符串aabaaa)，存在相同的最长真前缀aa与最长真后缀aa，字符串长度2，next[ 7 ] = 1 + 2 = 3

---

 

关于某个next[ i ] 的值求解，图解原理

以next[ 11 ] 为例，假设next[ 10 ] = 5

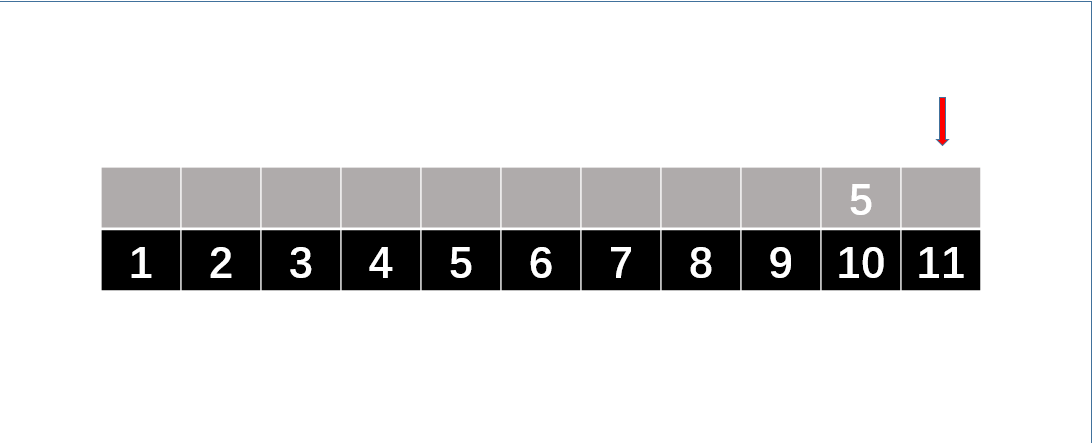
next[ 10 ] = 5，说明前面4个字符与后面4个字符相同，若此时模式串s[ 5 ]与s[ 10 ]相同，

则next[ 11 ] = next[ 10 ] + 1 = 6

 若next[ 5 ] 与next[ 10 ] 不相同，假设next[ 5 ] = 2，说明前面1个字符与后面一个字符相同

(即s[ 1 ] = s[ 4 ])，又因为两个红色矩形框部分字符相同，可推出，第二个红色矩形框内存在

s[ 6 ] = s[ 9 ]，即四个黑色矩形框内的字符相同

若此时s[ 2 ]与s[ 10 ] 相等，则next[ 11 ] = 2 + 1 = 3，若s[ 2 ] 与s[ 10 ] 不相同，继续递归操作

比较s[ 1 ]与s[ 10 ] 是否相同，相同则next[ 11 ] = 1 + 1 = 2，当比较到第一位字符时仍不相同，递归结束，next[ 11 ] = 1

---

 

 求解next数组代码

//计算next数组
void Next(SString T, int* next) {
	next[1] = 0;
	int j = 0;
	int i = 1;
	while (i < (int)(T[0])) {
		if (j == 0 || T[i] == T[j]) {
			i++;
			j++;
			next[i] = j;
		}
		else {
			j = next[j];
		}
	}
}

next 数组考虑的是除当前字符外的最长相同前缀后缀，即最长真前缀，当主串与模式串的某一位字符不匹配时，模式串回退next[ j ]位置继续比较，next[ j ]的值:第 j 为 位字符真前缀重合字符加1

 

仍以模式串aabaaab为例，求模式串的next数组

初始状态，i = 1，规定next[ 1 ] = 1，j = 0

执行第一次循环，满足 if 条件( j == 0)，此时 i 和 j 各增 1( i = 2，j = 1)，next[ 2 ] = j = 1

执行第二次循环，满足 if 条件( T[ i ] == T[ j ] )，此时 i 和 j 各增 1( i = 3，j = 2)，next[ 3 ] = j = 2

执行第三次循环，不满足 if 条件，进入else语句，j = next[ j ] = 1，执行第四次循环，同第三次，进入else语句，j = next[ j ] = 0

执行第五次循环，满足 if 条件( j == 0)，此时 i 和 j 各增 1( i = 4，j = 1)，next[ 4 ] = j = 1

执行第六次循环，满足 if 条件( T[ i ] == T[ j ] )， i 和 j 各增 1( i = 5，j = 2)，next[ 5 ] = j = 2

执行第七次循环，满足 if 条件( T[ i ] == T[ j ] )， i 和 j 各增 1( i = 6，j = 3)，next[ 6 ] = j = 3

执行第八次循环，不满足 if 条件，进入else语句，j = next[ j ] = 2

执行第九次循环，满足满足 if 条件( T[ i ] == T[ j ] )， i 和 j 各增 1( i = 7，j = 3)，next[ 7 ] = j = 3

算法很巧妙的在 if 条件语句中设置了 j == 0 这一条件，避免了访问模式串的数组越界，当满足该条件时，i 和 j 的值都增 1 

---

 

 KMP算法

当求得next数组后，在进行主串与模式串匹配的过程中，若出现的主串 i 位置不匹配时(此时模式串位于第 j 个位置)，不再回溯主串，而是移动模式串，取模式串中的第next[ j ] 位置继续同主串第 i个位置进行比较

int KMPIndex(SString S, SString T, int pos) {
	int i = pos;
	int j = 1;
	int next_arr[255];
	//获取串T中的next数组
	Next(T, next_arr);
	//Nextval(T, next_arr);
	while (i <= (int)(S[0]) && j <= (int)(T[0])) {
		if (0 == j || S[i] == T[j]) {
			i++;
			j++;
		}
		else {
			j = next_arr[j];
		}
	}
	//模式匹配成功
	if (j > (int)(T[0])) {
		return i - (int)(T[0]);
	}
	else {
		return 0;
	}
}

 

仍以模式串aabaaab为例，主串为abcaabaaabc，匹配的起始位置pos假设为1，获取的next数组

进入第一次循环，比较 i 和 j 所指字符是否相等，此时(i = 1，j = 1)，字符相等，满足 if 条件(主串S[ i ]  == T[ j ])，i 和 j 各增 1(i = 2，j = 2)

进入第二次循环，比较 i 和 j 所指字符是否相等，不相等，不满足 if 条件，进入else语句

此时 j = next[ j ] = 1

进入第三次循环，比较 i 和 j 所指字符是否相等，不相等，不满足 if 条件，进入else语句

此时 j = next[ j ] = 0

进入第四次循环， 满足 if 条件( j == 0 )，i 和 j 各增 1(i = 3，j = 1)

进入第五次循环，比较 i 和 j 所指字符是否相等，不相等，不满足 if 条件，进入else语句

此时 j = next[ j ] = 0

进入第六次循环， 满足 if 条件( j == 0 )，i 和 j 各增 1(i = 4，j = 1)

此后，直至循环结束，满足 if 语句，模式串匹配成功，返回相应索引坐标

---

 

next数组算法改进

前面定义的next数组仍存在一定的缺陷，例如模式串为aaaab同主串aabaaaab匹配时，当 i = 4

j = 4 时，S[ 4 ] ≠ T[ 4 ] ，但next数组的指示还需要进行 i = 4，j = 3； i = 4，j = 2； i = 4，j = 1；

这三次重复比较，对next数组进行改进

void Nextval(SString T, int* next) {
	next[1] = 0;
	int j = 0;
	int i = 1;
	//T[0]存储模式串的长度
	while (i < (int)(T[0])) {
		//若j == 0时，索引下移一位
		//判断前缀与后缀是否相等
		if (0 == j || T[i] == T[j]) {
			i++;
			j++;
			if (T[i] != T[j]) {
				next[i] = j;
			}
			else {
				next[i] = next[j];
			}
		}
		else {
			j = next[j];
		}
	}
}

仍以模式串aabaaab为例，此时求出的next数组的值分别为：0、0、2、0、0、3、2，这里不做过多赘述

---

 

Java方式实现KMP算法

class Solution {
    public int strStr(String haystack, String needle) {
        int n = haystack.length(), m = needle.length();
        for (int i = 0; i + m <= n; i++) {
            boolean flag = true;
            for (int j = 0; j < m; j++) {
                if (haystack.charAt(i + j) != needle.charAt(j)) {
                    flag = false;
                    break;
                }
            }
            if (flag) {
                return i;
            }
        }
        return -1;
    }
}