信号去噪黑科技5：matlab一键实现EEMD联合小波阈值去噪重构

主题：原创matlab一键实现EEMD联合小波阈值去噪重构

代码下载链接：https://mbd.pub/o/bread/mbd-Zp2ck55v

---

        在实际工程应用中，信号不可避免会被噪声污染，导致信号特征提取和分析变得困难。今天给大家分享一种高效的信号降噪方法——EEMD模态分解联合小波阈值去噪重构，并通过详细实验验证它的强大效果！

01、背景介绍

       传统的小波阈值降噪虽然能有效降低噪声，但在复杂噪声背景下往往存在信号失真问题。为了进一步提升去噪性能，我们引入了EEMD模态分解对信号进行分量处理，结合小波阈值方法，实现更精准的信号重构。

       这套方法特别适用于机械故障诊断、生物医学信号分析等需要高保真去噪的场景。

02、整体思路

       整体思路可以概括为三步：

       1、第一步：EEMD分解噪声信号将复杂信号自适应分解成若干个本征模态函数IMFs，方便后续筛选有用分量。

       2、第二步：基于相关性筛选重要分量计算每个IMF与原信号的皮尔逊相关系数，只保留相关性强的分量，初步去除噪声成分。

      3、第三步：小波阈值进一步降噪并信号重构对筛选后的分量进行小波阈值降噪处理，最终重构出高质量去噪信号。

       这种先分解+筛选+精细去噪的策略，能大幅提升信号净化能力。

03、信息介绍

       EEMD+小波阈值信号去噪重构，多指标多图版本，matlab代码，直接运行

    一、集合经验模态分解（EEMD）联合小波阈值信号去噪重构，多指标多图版本，matlab代码，直接运行；“阅读原文”主页还有ICEEMDAN、VMD、EMD、EEMD、MVMD+小波阈值信号去噪重构;

       二、仅本店有：附有说明文档，里面注明了各个主要信号分量字符的含义和位置（包含原始信号、含噪信号、小波去噪后信号、重构信号、联合去噪后信号）；

      三、仅本店有：附有详细的替换excel数据步骤和替换代码，可参考自行简单替换数据；

       四、代码整体包含：

        1、EEMD去噪(嵌套在联合去噪)：对原始信号进行EEMD分解，计算分解得到的各个IMF分量与原始信号的相关性系数，选取相关性系数高的IMF分量进行重构去噪。

        2、小波阈值去噪：对原始信号进行小波阈值去噪，可以设置小波分解层数以及小波函数还有阈值估计方法（启发式阈值、自适应阈值、固定阈值、极大极小阈值）以及软硬阈值的设置，并对其画图。

        3、EEMD+小波阈值联合去噪：首先对原始信号进行EEMD分解，然后对分解出来的各个IMF分量进行相关性计算，然后对各个IMF分量进行小波阈值去噪，最后对去噪完的IMF分量进行相加重构完成去噪。

      五、评价指标

     原始信号/小波阈值去噪/EEMD+小波阈值联合去噪均有以下指标，方便对比，很全的指标：

     1、SNR信噪比

     2、PSNR峰值信噪比

     3、SSIM结构相似性指数

     4、MAE平均绝对误差

     5、RMSE均方根误差

     6、相关系数

04、实验流程

      本次实验以合成信号为例（包含调制信号、阻尼信号与正弦成分），具体流程如下：

      1、信号构建与加噪

   （如果你的信号本身含噪，可直接替换，附送有文档，里面有直接替换代码，复制即可）：

      采样频率4000Hz，生成组合信号，并叠加标准差为0.2的高斯白噪声。

      2、EEMD分解：

      设置加噪次数100次，最大迭代100次，完成IMF分解。

      3、相关性筛选：

    选择相关系数大于0.4的IMF进行重构。

      4、小波阈值降噪：

      采用db4小波基进行3层分解，使用固定阈值规则处理细节系数。

      5、信号重构与对比：

      绘制时域图、频域图，对比原始、小波降噪和联合去噪后的效果。

05、图例展示

   生成图例展示：

       1、原始信号时域波形、含噪信号频谱

       2、模态时频图

       3、模态分量频谱图

       4、时域波形对比图（原始信号、含噪信号、小波降噪后信号、联合去噪后信号）

       5、频谱图对比（原始信号、含噪信号、小波降噪后信号、联合去噪后信号）

       6、三信号指标SNR、PSNR、SSIM、MAE、RMSE、相关系数对比图

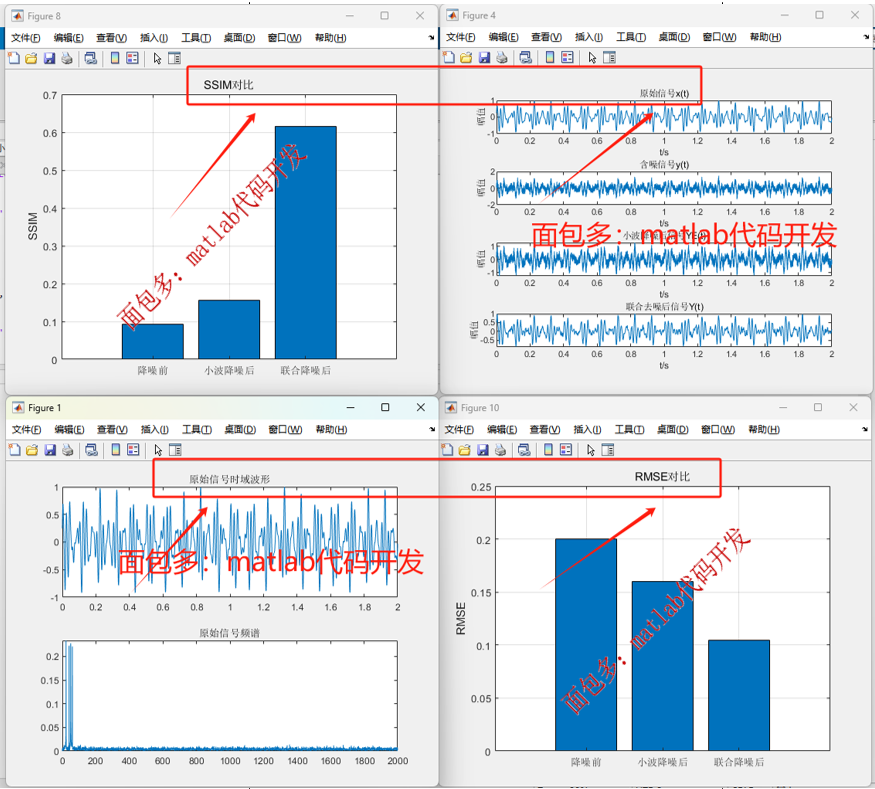
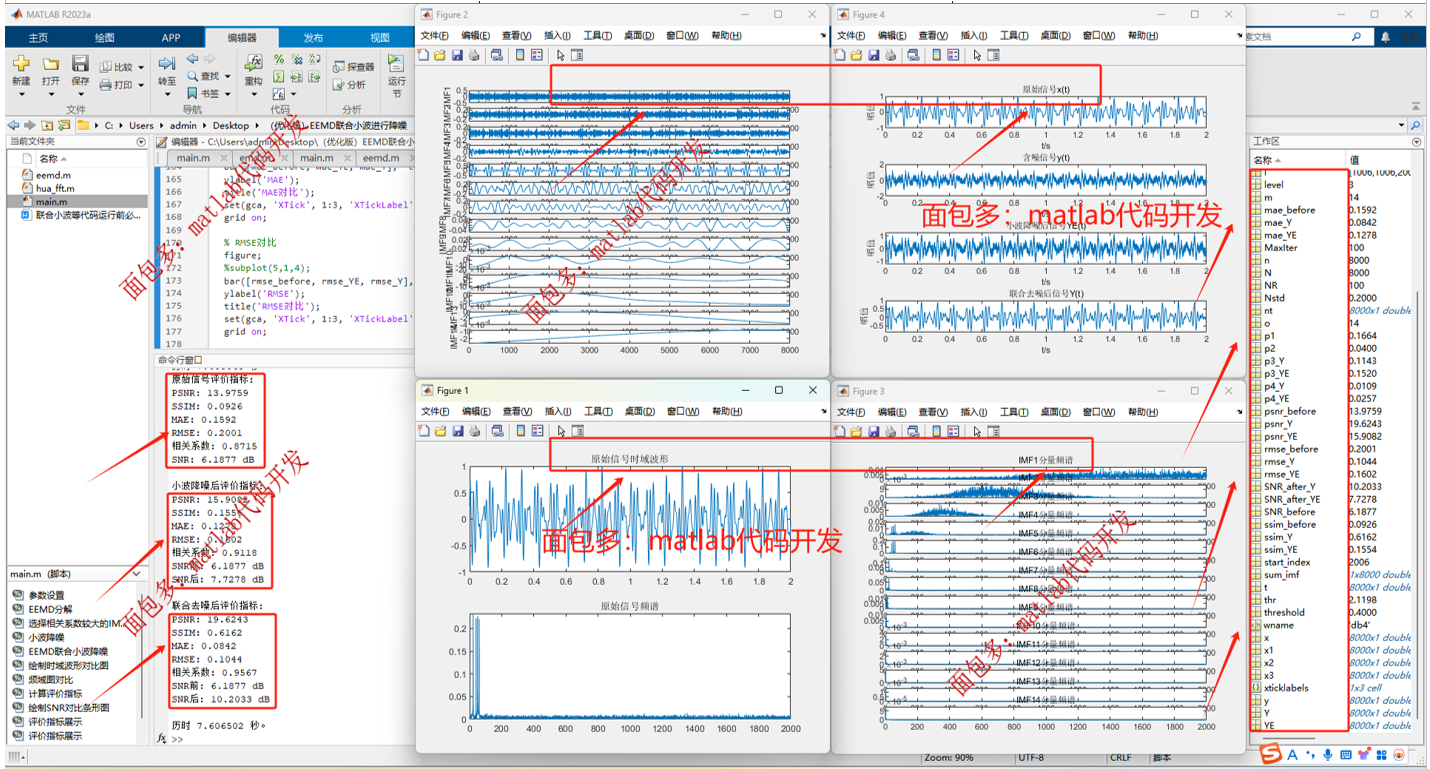
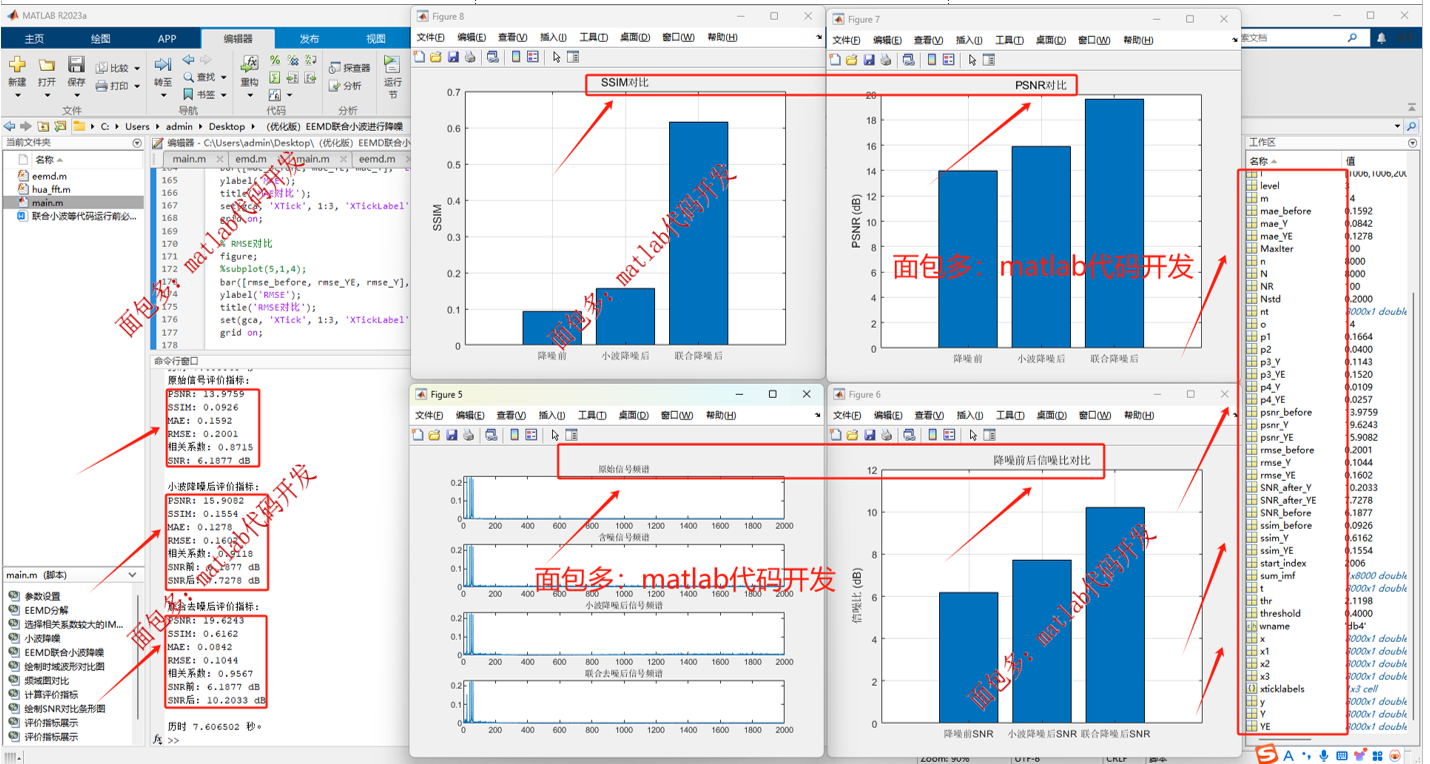
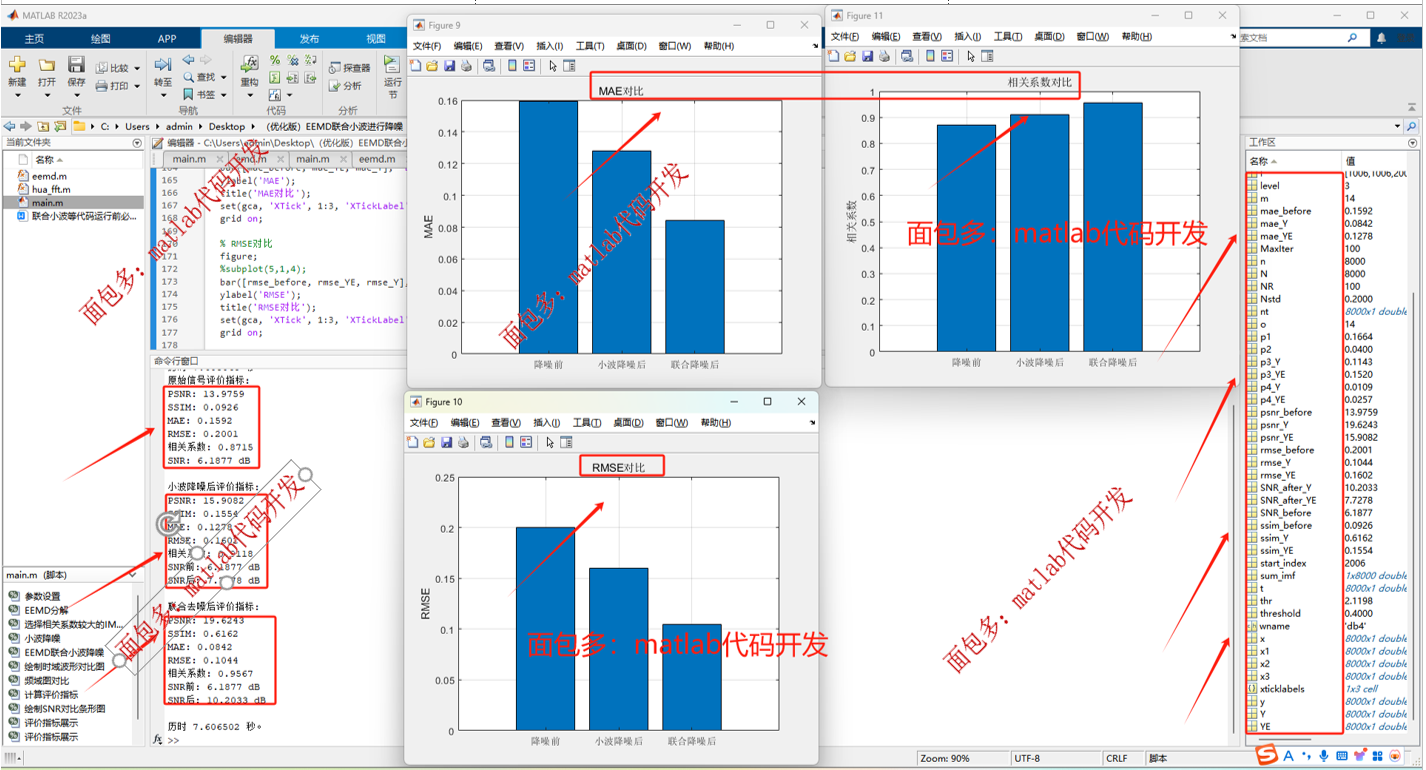
06、结果分析

       通过一系列评价指标，直观展示了去噪效果，具体见展示图例和6项评价指标。

       1- 可以看到，联合去噪在各项指标上均显著优于单独的小波降噪，大大提升了信号还原质量。

       2-此外，频谱图和时域波形对比也进一步印证了联合方法在噪声抑制和信号保真方面的优势。

07、总结与展望

       EEMD联合小波阈值去噪，充分结合了时频局部特性分析和多尺度分解能力，在复杂噪声背景下展现出优秀的降噪性能。未来可以将这套方法拓展到：

       1、机械故障振动信号分析

       2、生物医学如脑电、心电信号降噪

       3、声学、地震数据处理等领域

      如果你也在寻找一种精细且鲁棒的信号去噪方案，不妨一试这套方法！

      觉得有用的话，欢迎点赞、收藏、转发哦！前往主页查看更多降噪玩法，VMD、EMD、EEMD、CEEMDAN、ICEEMDAN、MVMD+小波联合阈值去噪！！！

---

代码经营范围：

 各类故障诊断研究、智能优化算法、神经网络分类/时序/回归、熵值特征分析、优化模态分解、聚类算法、数据去噪重构、数据特征提取等等，持续更新中！！！