算法竞赛系列 | 堆

本文适合初级和中级学习：刚学过编程语言，正在学数据结构的编程新手；学过基础数据结构，但是对代码的掌握还不够熟练的读者。

PS: 与普通计算机教材相比，本书代码的写法很不一样，似乎不太正式，而是非常简洁。这是因为本书的主要读者是算法竞赛选手，他们在竞赛时需要简化代码、加快编码速度、把注意力放在算法实现上。例如使用一个大数组，普通教材的常见做法是动态分配一个空间，使用完后释放。而本书的代码省略了分配和释放，直接定义一个全局的静态大数组，例如int a[1000000]。

堆是一种树形结构，树的根是堆顶，堆顶始终保持为所有元素的最优值。有最大堆和最小堆，最大堆的根节点是最大值，最小堆的根节点是最小值。本节都以最小堆为例进行讲解。堆一般用二叉树实现，称为二叉堆。二叉堆的典型应用有堆排序和优先队列。

01

二叉堆概念

二叉堆是一棵完全二叉树。用数组实现的二叉树堆，树中的每个节点与数组中存放的元素对应。树的每层，除了最后一层可能不满，其他都是满的。如图1.10所示，用数组实现一棵二叉树堆。

■ 图1.10用数组实现的二叉树堆

二叉堆中的每个节点，都是以它为父节点的子树的最小值。

用数组A［］存储完全二叉树，节点数量为n，A［1］为根节点，有以下性质：

(1) i>1的节点，其父节点位于i/2；

(2) 如果2i>n，那么节点i没有孩子；如果2i+1>n，那么节点i没有右孩子；

(3) 如果节点i有孩子，那么它的左孩子是2i，右孩子是2i+1。

堆的操作有进堆和出堆。

(1) 进堆：每次把元素放进堆，都调整堆的形状，使根节点保持最小。

(2) 出堆：每次取出的堆顶，就是整个堆的最小值；同时调整堆，使新的堆顶最小。

二叉树只有O(log2n)层，进堆和出堆逐层调整，计算复杂度都为O(log2n)。

02

二叉堆的操作

堆的操作有两种：上浮和下沉。

1. 上浮

某个节点的优先级上升，或者在堆底加入一个新元素(建堆，把新元素加入堆)，此时需要从下至上恢复堆的顺序。图1.11演示了上浮的过程。

■ 图1.1  新元素2的上浮

2.下沉

某个节点的优先级下降，或者将根节点替换为一个较小的新元素(弹出堆顶，用其他元素替换它)，此时需要从上至下恢复堆的顺序。图1.12演示了下沉的过程。

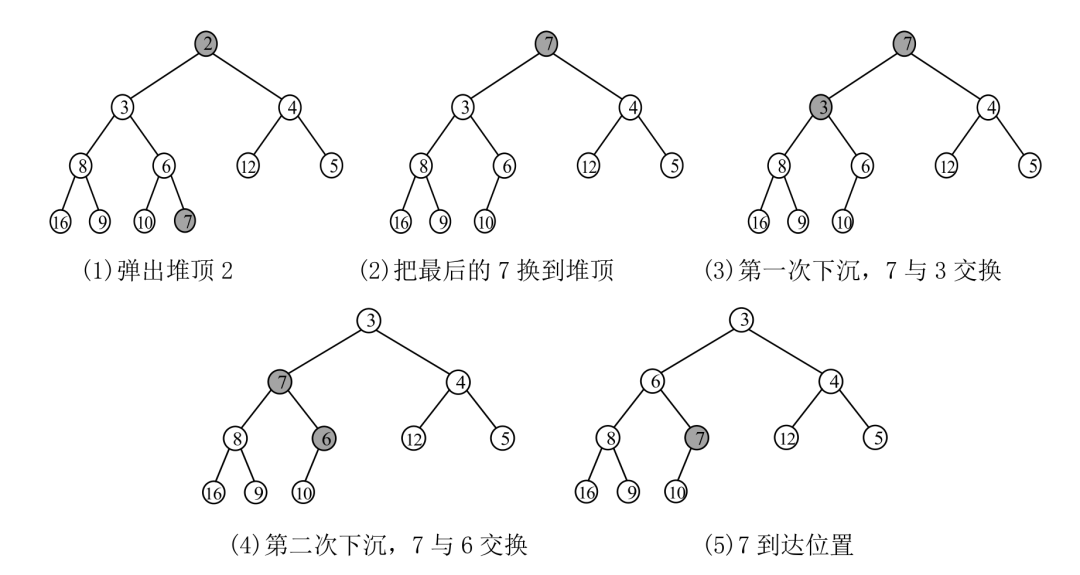
■ 图1.12弹出堆顶后，元素7的下沉

堆经常用于实现优先队列，上浮对应优先队列的插入操作push()，下沉对应优先队列的删除队头操作pop()。

03

二叉堆的手写代码

本节通过例题给出手写堆的实现，类似的题目还有洛谷P2278。

● 例1.8堆(洛谷P3378)

问题描述：初始小根堆为空，需要支持以下3种操作： 

操作1：输入1 x，表示将x插入堆中；

操作2：输入2，输出该小根堆内的最小数；

操作3：输入3，删除该小根堆内的最小数。

输入：第1行输入一个整数N，表示操作的个数，N≤1000000；接下来N行中，每行输入一或两个正整数，表示3种操作之一。

输出： 对于每个操作2，输出一个整数表示答案。

下面给出代码。上浮用push()函数实现，完成插入新元素的功能，对应优先队列的入队；下沉用pop()函数实现，完成删除堆头的功能，对应优先队列的删除队头。

#include<bits/stdc++.h>using namespace std;const int N = 1e6 + 5;int heap[N], len=0;                 //len记录当前二叉树的长度void push(int x) {                  //上浮，插入新元素     heap[++len] = x;     int i = len;     while (i > 1 && heap[i] < heap[i/2]){  swap(heap[i], heap[i/2]);   i = i/2;         }}void pop() {                         //下沉，删除堆头，调整堆     heap[1] = heap[len--];           //根结点替换为最后一个结点，然后结点数量减1     int i = 1;     while ( 2*i <= len) {            //至少有左儿子        int son = 2*i;                //左儿子if (son < len && heap[son + 1] < heap[son])  son++;                    //son<len表示有右儿子，选儿子中较小的        if (heap[son] < heap[i]){                   //与小的儿子交换             swap(heap[son], heap[i]); i = son;                 //下沉到儿子处        }        else break;                  //如果不比儿子小，就停止下沉    }}int main() {    int n;   scanf("%d",&n);    while(n--){        int op;  scanf("%d",&op);        if (op == 1) { int x;  scanf("%d",&x); push(x); }  //加入堆            else if (op == 2)  printf("%d\n", heap[1]);        //打印堆头        else pop();                                        //删除堆头    }    return 0;}

04

堆和priority_queue

STL的优先队列priority_queue是用堆实现的。下面给出洛谷P3378的STL代码，由于不用自己管理堆，代码很简洁。​​​​​​​

#include<bits/stdc++.h>using namespace std;priority_queue<int ,vector<int>,greater<int> >q;  //定义堆int main(){    int n;  scanf("%d",&n);    while(n--) {        int op;   scanf("%d",&op);        if(op==1) { int x;   scanf("%d",&x);  q.push(x); }        else if(op==2)   printf("%d\n",q.top());        else  q.pop();    }    return 0;}

小结

基本数据结构是算法大厦的基石，它们渗透在所有问题的代码实现中。不存在“是否应该掌握好基本数据结构”的疑问，程序员应该能不假思索、条件反射般地手写出来。初学者应在后续内容学习时有意识地加强基本数据结构的编程练习。

需要重点指出的是，本系列介绍的链表、堆等基本数据结构，在竞赛中可以用STL实现，也可以手写代码。STL是参赛者需要重点掌握的，大多数题目用到的基本数据结构都能直接用STL实现，编码简单快捷，不容易出错。如果手写，一般都使用静态数组来模拟。虽然用静态数组模拟不太符合正规的软件工程的做法，但是在竞赛中这样编程快且不易出错。

《算法竞赛》系列推文正在连载中，欢迎持续关注！