广州交通大学二年级算法实验题目（第一弹）

---

写在前面

这个学期学院给我们专业开了算法课，下星期五是专业第一次算法实验课，晚上老师给我们先发了实验内容让我们去准备，题目有这些：

必选题：1.归并排序 2.棋盘覆盖
自选题：3.找众数 4.半数集 5.重复元素的全排列 6. 整数因子分解
附加题：7.快速排序 8.线性时间选择

现在是清明节放假的第一天，因为感觉回家路太堵，也只有短短三天，索性留在学校，昨晚把题目都看了一遍，觉得并没有太难，写完之后今天再来整理一下。

吐槽一下学校的图书馆，很热，去到四楼发现插座没有电，底楼在装修，整栋楼都是噪音，倒霉啊。辗转来了煎饼楼，没有WIFI，将就将就。

---

内容:

这是一个链接 >几分钟初步学会归并排序和快速排序<

归并排序和快速排序可以看我之前的这篇文章，（虽然写得不怎么样），其余的题目我就按上面的顺序放过来。

2. 棋盘覆盖

给你一个有2^k * 2^k（k = 2, 3, 4…）个方格的棋盘，此棋盘上恰有一个特殊方格，用以下四种类型的L型骨牌，覆盖棋盘上除特殊方格以外的区域。

一看，2 * 2 或 4 * 4不是很简单？如果k超级大？嗯…但我还是可以将这个大棋盘切成很多个2 * 2的小棋盘的吧。（递归yyds）

这样思路就来了：假设棋盘是8 * 8，我可以先将它分为四个 4 * 4的棋盘（象限1,2,3,4），然后判断特殊方格所在的象限，将此象限继续切成四个2 * 2的棋盘，进入递归。但为了将另外三个普通棋盘转化为特殊棋盘，我们可以用一个L型骨牌覆盖这3个较小棋盘的汇合处，这三个普通棋盘上被L型骨牌覆盖的方格就成为该棋盘上的特殊方格，从而成功将大特殊棋盘8 * 8分为四个小特殊棋盘4 * 4，继续按照此方式切分，直至棋盘变成1 * 1。
                            
看了一下书上的伪码传参，分别是记录棋盘左上角方格的行列数tr、tc（定位棋盘），还有定位特殊方格所在的行列dr、dc，接着是棋盘的大小size。我另外引入了棋盘的二维数组，然后开始写代码。

public class Main{
	static int num = 1;
    public static void chessBoard(int[][] board, int tr, int tc, int dr, int dc, int size){
    	int dividesize = size / 2;
    	int currentNum = num++;
    	if (dividesize == 1) {
    		return;
    	}
    	// 象限1
    	if (dr < dividesize + tr && dc >= dividesize + tc) {
    		chessBoard(board, tr, tc + dividesize, dr, dc, dividesize);
    	}else {
    		board[dividesize - 1 + tr][dividesize + tc] = currentNum;
    		chessBoard(board, tr, tc + dividesize, dividesize - 1 + tr, dividesize + tc, dividesize);
    	}
    	// 象限2
    	if (dr < dividesize + tr && dc < dividesize + tc) {
    		chessBoard(board, tr, tc, dr, dc, dividesize);
    	}else {
    		board[dividesize - 1 + tr][dividesize - 1 + tc] = currentNum;
    		chessBoard(board, tr, tc, dividesize - 1 + tr, dividesize - 1 + tc, dividesize);
    	}
    	// 象限3
    	if (dr >= dividesize + tr && dc < dividesize + tc) {
    		chessBoard(board, tr + dividesize, tc, dr, dc, dividesize);
    	}else {
    		board[dividesize + tr][dividesize - 1 + tc] = currentNum;
    		chessBoard(board, tr + dividesize, tc, dividesize + tr, dividesize - 1 + tc, dividesize);
    	}
    	// 象限4
    	if (dr > dividesize + tr && dc > dividesize + tc) {
    		chessBoard(board, tr + dividesize, tc + dividesize, dr, dc, dividesize);
    	}else {
    		board[dividesize + tr][dividesize + tc] = currentNum;
    		chessBoard(board, tr + dividesize, tc + dividesize, dividesize + tr, dividesize + tc, dividesize);
    	}
    }
    public static void main(String[] args){
		int[][] board = new int[8][8];
		chessBoard(board, 0, 0, 0, 3, 8);
		for (int i = 0; i < board.length; ++i) {
			for (int j = 0; j < board[0].length; ++j) {
				System.out.print(board[i][j] + "\t");
			}
			System.out.println();
		}
	}
}  

写到这，已经经过了不知道多少次的调试、改传参，调了差不多半小时，头晕脑胀。然而测试结果是这个样子：

再看一眼书上，代码确实是这样没错，是打开姿势不对吗，我细想一番，决定在递归出口再加一些代码：

    	if (dividesize == 1) {
    		// 象限1
        	if (dr != tr || dc != tc + 1) {
        		board[tr][tc + 1] = currentNum;
        	}
        	// 象限2
        	if (dr != tr || dc != tc) {
        		board[tr][tc] = currentNum;
        	}
        	// 象限3
        	if (dr != tr + 1 || dc != tc) {
        		board[tr + 1][tc] = currentNum;
        	}
        	// 象限4
        	if (dr != tr + 1 || dc != tc + 1) {
        		board[tr + 1][tc + 1] = currentNum;
        	}
    		return;
    	}

运行：

… 书上并没有这段代码，去网上找帖子，发现很多也没有这一段，这是为啥…唉，先把问题放一放，有好兄弟懂的话评论区教一下俺这个小菜鸡…

好！下一题！

---

9.32更新， 问题代码修改：

public class chessBoard {
        static int num = 1;
        public static void chessBoard(int[][] board, int tr, int tc, int dr, int dc, int size){
            if (size == 1) {
                return;
            }
            int dividesize = size / 2;
            int currentNum = num++;
            // 象限1
            if (dr < dividesize + tr && dc >= dividesize + tc) {
                chessBoard(board, tr, tc + dividesize, dr, dc, dividesize);
            }else {
                board[dividesize - 1 + tr][dividesize + tc] = currentNum;
                chessBoard(board, tr, tc + dividesize, dividesize - 1 + tr, dividesize + tc, dividesize);
            }
            // 象限2
            if (dr < dividesize + tr && dc < dividesize + tc) {
                chessBoard(board, tr, tc, dr, dc, dividesize);
            }else {
                board[dividesize - 1 + tr][dividesize - 1 + tc] = currentNum;
                chessBoard(board, tr, tc, dividesize - 1 + tr, dividesize - 1 + tc, dividesize);
            }
            // 象限3
            if (dr >= dividesize + tr && dc < dividesize + tc) {
                chessBoard(board, tr + dividesize, tc, dr, dc, dividesize);
            }else {
                board[dividesize + tr][dividesize - 1 + tc] = currentNum;
                chessBoard(board, tr + dividesize, tc, dividesize + tr, dividesize - 1 + tc, dividesize);
            }
            // 象限4
            if (dr > dividesize + tr && dc > dividesize + tc) {
                chessBoard(board, tr + dividesize, tc + dividesize, dr, dc, dividesize);
            }else {
                board[dividesize + tr][dividesize + tc] = currentNum;
                chessBoard(board, tr + dividesize, tc + dividesize, dividesize + tr, dividesize + tc, dividesize);
            }
        }
        public static void main(String[] args){
            int[][] board = new int[8][8];
            chessBoard(board, 0, 0, 0, 3, 8);
            for (int i = 0; i < board.length; ++i) {
                for (int j = 0; j < board[0].length; ++j) {
                    System.out.print(board[i][j] + "\t");
                }
                System.out.println();
            }
        }
    }

---

3. 找众数

给定一个数组（乱序），找出其中的众数（出现次数最多的数）和重数（众数的个数）。这题就很简单啦！先排序，再一次遍历，注意边界条件：数组以众数结尾或者非众数结尾。

    public static int[] searchMode(int[] nums){
    	if (nums.length == 0) {
    		return nums;
    	}
    	Arrays.sort(nums);
    	int count = 0, maxCount = 0,mode = nums[0];
    	for (int i = 0; i < nums.length - 1; ++i) {
    		if (nums[i] == nums[i + 1]) {
    			count++;
    			if (i == nums.length - 2 && count >= maxCount) {// 以众数结尾
    				mode = nums[i];    // 记录众数
        			maxCount = ++count;// 记录重数
    			}
    		}else if (count >= maxCount) { // 不以众数结尾
    			mode = nums[i];  // 记录众数
    			maxCount = count;// 记录重数
    			count = 0;
    		}
    	}
    	return new int[] {mode, maxCount};
    }

虽然简单，但我觉得写得有亿点乱唉…复杂度是 O（n）。

但有没有不排序的路子呢？我想应该是有的，遍历第一次数组，用HashMap的key记录元素值，用HashMap的value记录元素出现次数，然后找出HashMap里value最大的key，我想应该可以，这里鸽掉，嘿嘿。

---

9.32更新：解法2

    public static int[] searchMode(int[] nums){
        int mode = 0, modeNum = 0;
        // 定义哈希表，key对应众数，value对应重数
        Map<Integer, Integer> map = new HashMap<Integer, Integer>();
        for (int i = 0; i < nums.length; ++i) {
            if (map.containsKey(nums[i])) {// 已存在key，将value加1
                map.put(nums[i], map.get(nums[i]) + 1);
            }else{// 不存在key，加入key将value设置为1
                map.put(nums[i], 1);
            }
            if (map.get(nums[i]) > modeNum) {
                mode = nums[i];// 获得众数
                modeNum = map.get(nums[i]);// 获得重数
            }
        }
        return new int[] {mode, modeNum};
    }

---

4. 半数集

经典递归题，只要好好审题，代码就不难理解。

半数集定义：

现要求传入参数n，求出半数集set（n）中元素个数。

	//半数集
    public static int comp(int n){
    	int ans = 1;
    	if (n > 1) {
    		for (int i = 1; i <= n / 2; i++) {
    			ans += comp(i);    			
    		}    		
    	}
    	return ans;
    }

光看代码想起来难，建议cv去debug，看看参数怎么传的。

路子大概就是传参为6的空间下有comp（1）、comp（2）、comp（3），然后这三个分别的子空间里：comp（1）没有直接返回ans = 1，comp（2）有comp（1），comp（3）有comp（1）…

最后传回comp（6）的空间中：
comp（1）= 1，comp（2） = 2，comp（3） = 2，再加上ans默认值1，返回6.所以半数集set（6）里有6个元素。

好家伙，不会有人看懂我在讲什么吧，写完我自己都不知道自己在讲什么233。

---

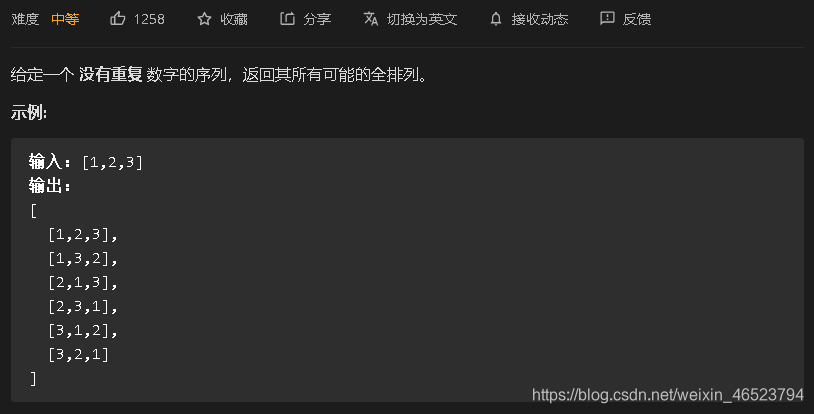
5. 重复元素的全排列

就是力扣的全排列2，在全排列1的基础上加上了原数组含有重复元素，所以首先要明白没有重复元素时候，全排列怎么求。

我们使用深度优先搜索dfs，配合回溯（状态重置）与剪枝（收集答案）

（上面偷力扣君视频里的一张截图，力扣君yyds）

黄色部分表示我们的深度优先搜索深度已经到达数组长度，此时进行剪枝（保存一个答案），例如【1、2、3】，然后撤销当前操作，把3移出数组，再把2移出数组。再接着选3、再选2，形成【1、3、2】，如此类推。

关键是怎么撤销和保存答案，用到了这几个状态变量：
path（栈：记录路径），used[]（标记已经使用的元素），deepth（搜索深度）

全排列到此就完成啦！但这个代码显然不能解决含有重复元素的问题，怎么办呢。很简单，只要事先将数组进行排序，保证重复元素都在相邻位置，然后在dfs里面循环的if语句中加入下面的条件：

   if(used[i] || (i > 0 && nums[i] == nums[i - 1] && !used[i - 1])){
      continue;
   }
            

一：i > 0:

1. 防止溢出

二：nums[i] == nums[i - 1] :

1. 保证重复序列首元进入
2. 限制以除重复序列首元外的元素为首的递归进入

三：!used[i - 1] :

1. 保证以首元开始的递归进行

完整代码：

class Solution {
    public List<List<Integer>> permuteUnique(int[] nums) {
        Arrays.sort(nums);
        List<List<Integer>> res = new ArrayList<>();
        if (nums.length == 0){
            return res;
        }
        //状态变量path（栈），used[]，deepth
        Deque<Integer> path = new ArrayDeque<>();
        boolean[] used = new boolean[nums.length];
        int deepth = 0;
        dfs(nums, res, path, used, deepth);
        return res;
    }
    private void dfs(int[] nums, List<List<Integer>> res, Deque<Integer> path, boolean[] used, int deepth) {
        if (deepth == nums.length){//“剪枝”
            res.add(new ArrayList<>(path));
            return;
        }
        for (int i=0; i<nums.length; ++i){
            // nums[i] == nums[i - 1] 
            // 保证重复序列首元进入、限制以除重复序列首元外的元素为首的递归进入
            // !used[i - 1]
            // 保证以首元开始的递归进行
            if(used[i] || (i > 0 && nums[i] == nums[i - 1] && !used[i - 1])){
                continue;
            }
            path.addLast(nums[i]);
            used[i] = true;
            dfs(nums, res, path, used, deepth+1);
            path.removeLast();//状态重置
            used[i] = false;
        }
    }
}

---

6. 整数因子分解

这是书上练习的最后一题，我最喜欢的一题（可能是因为很快解出来2333）

问题描述：
大于1的正整数n可以分解为
$$n=a\ast b\ast c\ast ...\ast z$$
当n = 6时，有3种不同的分解式：
$$6=6，6=2\times 3，6=3\times 2$$
对于给定的正整数n，计算有多少种不同的分解式。

这里用到判断一个数是不是质数的算法思想，我们很快可以想到双重遍历，但其实只需要从2开始，到n的平方根即可。因为假设a×b=n，若a比n的平方根小，那么b一定比n的平方根大，我们搜索到了a×b=n，自然也就存在b×a=n，就可以直接将种类数加2。而边界条件就是：n的平方根×n的平方根 = n，对于此边界条件，我们可以只将种数加1。

是不是一下子就明白了呢，但不要忘了一点，还可能是n = a×b×c ！但只要有上面的思想，我们可以将b递归下去，将b拆分成N个分解式，加入总数即可。

您的代码已到账，请注意查收~

---

8. 线性时间选择

在线性时间里，从乱序数组中找出第k小的数。

一开始不怎么明白是要做什么，可以看看书上这段话：

书上的伪码描述：

Type RandomizedSelect(Type[] a, int p, int r, int k) {
        if (p == r)
            return a[p];
        int i = RandomizedPartition(a, p, r);
        j = i - p + 1;
        if (k <= j)
            return RandomizedSelect(a, p, i, k);
        else
            return RandomizedSelect(a, i + 1, r, k - j);
    }

我基于此用快排实现的代码：

import java.util.*;
import java.io.File;
import java.io.PrintWriter;
import java.io.FileNotFoundException;

public class Main{
    public static int randomizedSelected(int[] a, int p, int r, int k){
    	if (p == r) {
    		return a[p];
    	}
    	int i = randomizedPartition(a, p, r);
    	int j = i - p + 1;
    	if (k <= j) {
    		return randomizedSelected(a, p, i, k);
    	}else {
    		return randomizedSelected(a, i + 1, r, k - j);
    	}
    }
    public static int randomizedPartition(int[] a, int p, int r) {
    	// 基于快排的一次基准归位
 	    int i = p, j = r, base = a[p];
 	    while (i < j) {
 	        while (a[j] >= base && j > i) {
 	        	--j;
 	        }
 	        while (a[i] <= base && i < j) {
 	        	++i;
 	        }
 	        if (i < j) {
 	        	int temp = a[j];
 	        	a[j] = a[i];
 	        	a[i] = temp;
 	        }
 	    }
 	    a[p] = a[i];
 	    a[i] = base;
 	    return i;
    }
    public static void main(String[] args){
		int[] nums = new int[] {4, 5, 3, 2, 1};
		System.out.print(randomizedSelected(nums, 0, nums.length - 1, 5));			
	}
}

与快排不同的是，每一次基准数归位找出i，需要比较一次i与k的关系，若找到了第k小的元素即刻返回，未找到就继续下一次的基准归位。
（书上说每次归位的基准数下标需要取随机值（未实现））

---

写在最后

整理完这第一波实验题，觉得并没有说非常难。

这次也是一个标题党，我摊牌了，想骗大佬们的一键三连。现在已经是中午时分，肚子饿得咕咕叫，收拾好电脑去干饭。听老师说这门课一共有三次实验，不知道下一次实验又会学到什么新东西呢？朋友说明天图书馆闭馆，唉…

好了，下次见！