李宏毅机器学习（2021版）_P5-6：小梯度处理

北海虽赊，扶摇可接

已于 2022-07-24 15:26:44 修改

阅读量406

点赞数 1

分类专栏：李宏毅机器学习（2017版）文章标签：机器学习算法人工智能

于 2022-07-20 20:14:33 首次发布

本文链接：https://blog.youkuaiyun.com/weixin_46336048/article/details/125898496

版权

李宏毅机器学习（2017版）专栏收录该内容

9 篇文章

订阅专栏

1、优化失败原因 Optimization Fails

在这里插入图片描述

1.1、critical point

gradient is zero，梯度为0的点，称为critical point。包含两类，local minima，saddle point，如下：
在这里插入图片描述

1.2、数学解释

采用多元函数泰勒展开，𝐿（𝜽）在𝜽 = 𝜽′处展开如下：
在这里插入图片描述
g为函数梯度，为一个向量；H为函数的海森矩阵，表示对不同参数的二阶矩阵：

在critical point处，梯度g=0，简化如下：

Critical Point类型有三类，minima，maxima，Saddle point，依靠 $𝒗^𝑇𝐻𝒗$ 大小判断：
$𝒗^𝑇𝐻𝒗$ >0：𝐿(𝜽)> 𝐿(𝜽′)，minima
$𝒗^𝑇𝐻𝒗$ <0：𝐿(𝜽)< 𝐿(𝜽′)，maxima
$𝒗^𝑇𝐻𝒗$ >0 及 <0：Saddle point
也可以通过H的特征值正负性判断三类特殊点。在这里插入图片描述 举例： $𝑦 = 𝑤_1𝑤_2𝑥$ ，数据（1,1）
损失函数： $(\hat𝑦 − 𝑤_1𝑤_2𝑥)^2 = (1- 𝑤_1𝑤_2)^2$ ;
计算g与H如下：

1.3、鞍点处理

依靠海森矩阵H确定鞍点优化方向，𝐻 may tell us parameter update direction。数学的假设推理如下：
在这里插入图片描述
寻找海森矩阵H的一个负的特征向量u，即为L下降方向。
举例：
上述函数，找到鞍点并且寻找下降方向：

在（0,0），海森矩阵H特征值2，-2。有正负，判断（0,0）为鞍点。
选取海森矩阵H特征值-2对应的一个特征向量𝒖 = [1, 1]，即为更新方向。
但是，因为计算量比较大，上述方法比较少用。

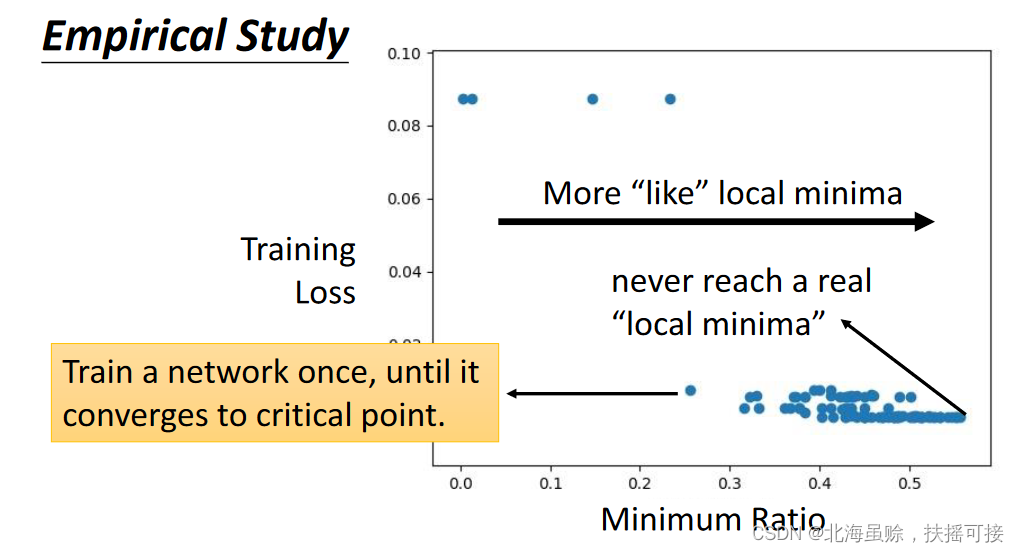
1.4、临界点数量比例

在这里插入图片描述
$\frac {Number \; of \; Positive \; Eigen \;values} {Number\; of \;Eigen \;values}$
上图中，通过实证研究，大部分的critical point为鞍点，local minima很少(横坐标1处，为绝对minima)。

2、Batch and Momentum

2.1、Batch 批次

一个训练epoch分为数个batch，每一个batch均可以对损失函数参数 $\theta$ 进行更新。每个epoch的batch均会重新分配。
在这里插入图片描述

2.2、Small Batch v.s. Large Batch

2.2.1、计算速度

采用GPU并行计算，小批次和大批次在一定范围内耗时基本一致：
在这里插入图片描述
但是不同batch之间转换需要更多时间，所以小批次epoch内需要时间更长：

2.2.2、训练优化效果

大批次训练，容易导致优化错误（Optimization Fails）；小批次训练性能更好：
在这里插入图片描述
原因：大批次参数更新次数少，容错率低；小批次参数更新的次数多，可以有更多可能跳出local minima。

2.2.3、测试检测效果

小批量测试数据要好，实验结果如下：SB表示小批次，LB表示大批次。
在这里插入图片描述
原因仍然是参数更新的问题，train与test的损失函数，认为有一定平移；小批次更容易陷入Sharp Minima，无法更新：

2.2.4、综合比对

在这里插入图片描述

2.3、Momentum

Momentum：学习率动量，在更新参数时，不仅考虑函数的梯度，也考虑之前更新的各个梯度方向：
$𝒎^t = \lambda 𝒎^{t-1} − \eta 𝒈^{t-1}$
综合考虑梯度下降和学习率动量，参数更新如下：在这里插入图片描述
在计算中，可以发现，动量 $m^i$ 包含 $g^0$ 到 $g^i$ 的各个权重之和；
$𝒎^i = -(\lambda^{i-1} \eta g^0 + \lambda^{i-2} \eta^2 g^1+...+\lambda \eta^{i-1} g^{i-2})-\eta g^{i-1}$