【算法】旅行商问题——运行时间为O(n!)的算法

旅行商问题是一个运行时间极长的算法。这个算法是计算机科学领域非常著名的旅行商问题，其时间增长得非常快，而且即使非常聪明的人也没有改进空间。

旅行商问题是这样的：有一个旅行家，他需要前往5个城市。这位旅行商要前往5个城市，同时要确保旅程最短。为此，可考虑前往这些城市的各种可能顺序。

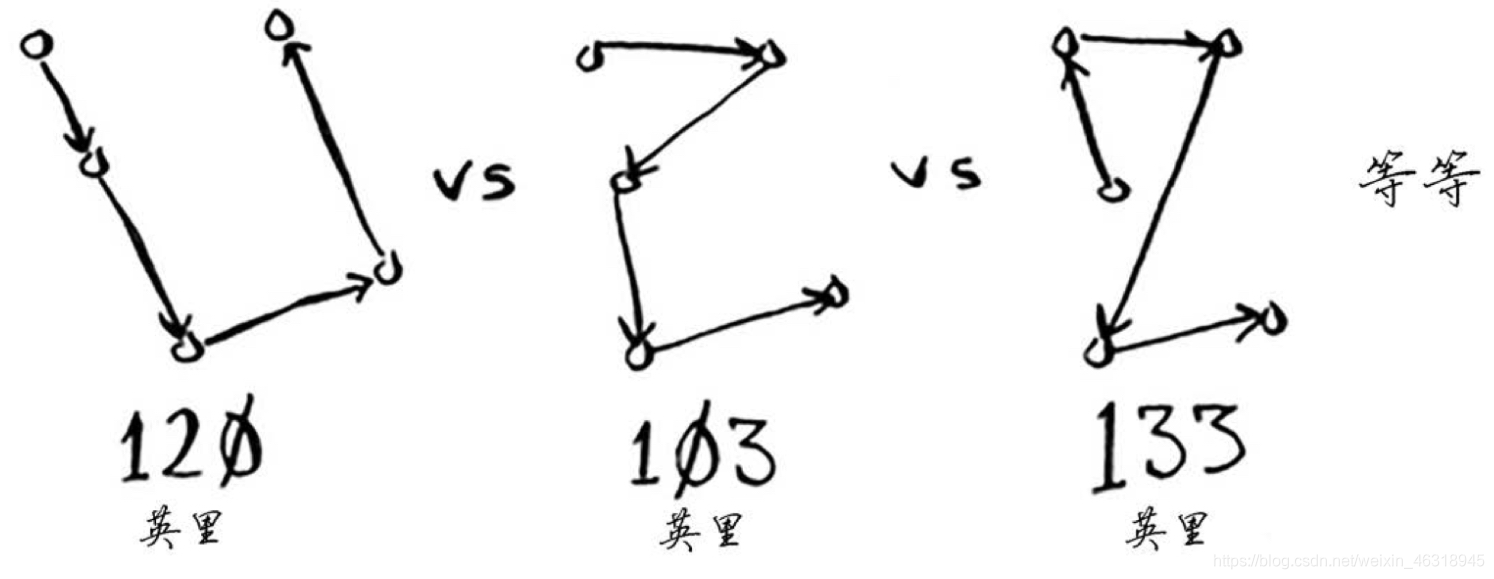
 对于每种顺序，他都计算总旅程，再挑出旅程最短的路线。5个城市有120种不同的排列方式。因此，在涉及5个城市时，解决这个问题需要执行120次操作。涉及6个城市时，需要执行720次操作（有720种不同的排列方式）。涉及7个城市，则需要执行高达5040次操作！

推而广之，涉及n个城市时，需要执行n!（n的阶乘）次操作才能获得结果。因此运行时间为O(n!)，即阶乘时间。除非涉及的城市数很少，否则需要执行非常多的操作。如果涉及的城市数超过100.根本就不能在合理的时间内计算出结果——等你计算出结果，太阳都没了。

这种算法的运行时间令人窒息，但别无选择。这是计算机科学领域亟待解决的问题之一，对于这个问题，目前还没有更快的算法，有些很聪明的