GAMES101-现代计算机图形学入门-闫令琪——Lecture 03 Transformation 学习笔记

Lecture 03 Transformation

一、2D transformations

（一）、Representing transformations using matrices

1、Scale (Non-Uniform) Matrix

2、Reflection Matrix

​

3、Shear Matrix

​

4、Rotation Matrix

旋转矩阵的推导过程：

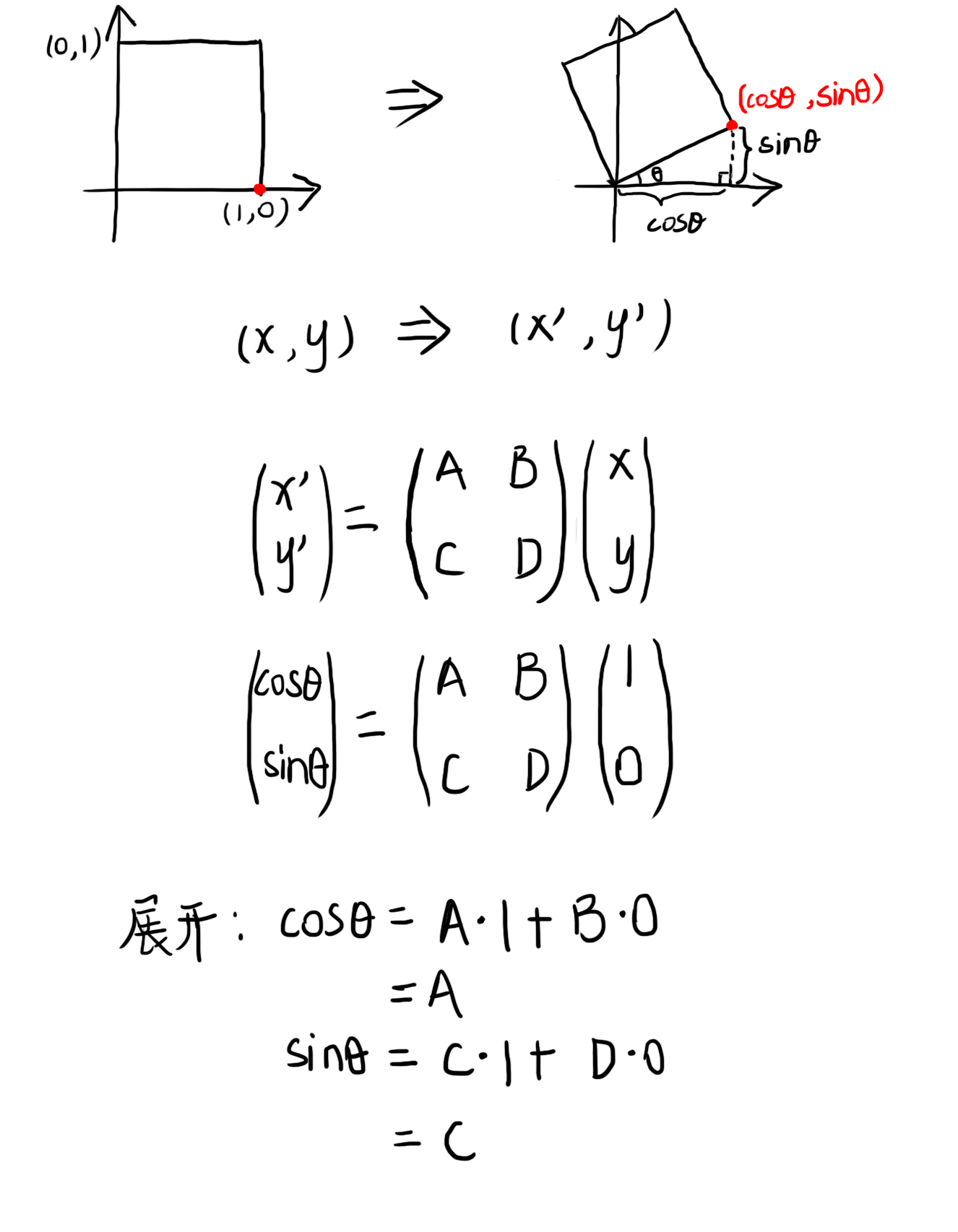
同理，B和D位置的推导选取点（0,1）即可

5、Linear Transforms = Matrices

以上的几种变换均属于线性变换，都可以用下列的公式表示

但是一旦涉及到移动，就无法通过上述的公式来实现了。

So, translation is NOT linear transform（因此我们可以看到，位移不属于线性变换）

• Translation cannot be represented in matrix form
• But we don’t want translation to be a special case
• Is there a unified way to represent all transformations? (and what’s the cost?)

如何将位移与前面提到的旋转、缩放等线性变换作一个统一？

我们引入了齐次坐标（下文）

（二）、Homogeneous coordinates

1、General Introduction

Add a third coordinate (w-coordinate)

我们通过在二维中引入第三个坐标w，将维度升高到三维，但是依然表示的是二维坐标。

• 2D point = (x, y, 1) ^T
• 2D vector = (x, y, 0)^T

引入齐次坐标后，我们再来看刚刚的位移，我们可以写成下面这个形式，其中t_x和t_y分别表示沿x轴和y轴的位移值

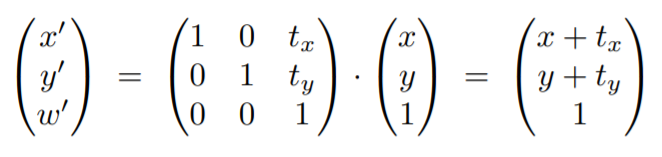
那么在上面我们为什么要区分2D point和 2D vector？原因如下：

Valid operation if w-coordinate of result is 1 or 0

• vector + vector = vector
• point – point = vector
• point + vector = point
• point + point = midpoint

这样可以满足一般的数学运算规律，例如两个向量相加结果依然为向量，即w=0，两个点相减结果为向量，此时w：1-1=0，点与向量相加（一个点沿着一个方向移动一段距离）结果仍为一个点，即w=1

• In homogeneous coordinates

要保持w的值始终为1，只需要将x和y同时除以w即可

2、2D Transformations

Affine map = linear map + translation

Using homogenous coordinates:

（1）Scale

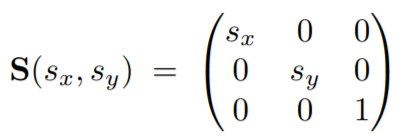
（2）Rotation

（3）Translation

3、Inverse Transform

M^-1 is the inverse of transform in both a matrix and geometric sense

逆变换在数学运算中即为逆矩阵

（三）Composing Transforms

将第一幅图变换到第二幅图有哪几种组合变换的方式呢？

第一种方式是先位移后旋转，显然结果并不是我们想要的，还有一种方式就是先旋转后位移。

通过这个案例我们也可以看出

• Matrix multiplication is not commutative（矩阵乘法是不能交换的）

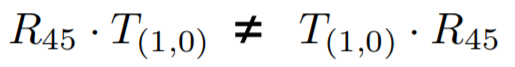
• Note that matrices are applied right to left（矩阵乘法是从右向左相乘的）

在一个组合变换中，虽然矩阵乘法不满足交换律，但是依然满足结合律

Sequence of affine transforms A1, A2, A3, …

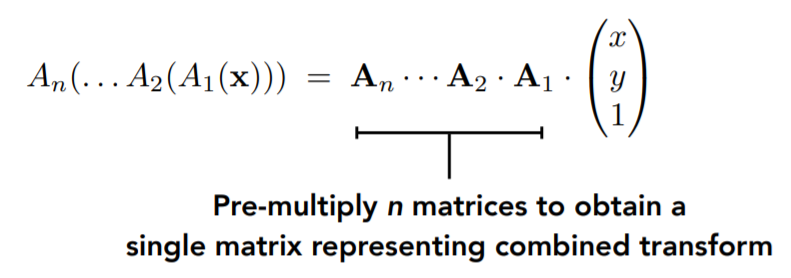
这也就意味着，无论经历了多少次变换，总能把所有变换计算出来写成一个总的变换矩阵