一、浣熊优化算法COA
浣熊优化算法(Coati Optimization Algorithm,COA)由Dehghani Mohammad等人于2022年提出的模拟浣熊狩猎行为的优化算法,该算法具有进化能力强,收敛速度快,收敛精度高等特点。
COA具体原理如下: 智能优化算法:浣熊优化算法-附代码_智能算法研学社(Jack旭)的博客-优快云博客
参考文献:Dehghani Mohammad, Montazeri Zeinab, Trojovská Eva, Trojovský Pavel. Coati Optimization Algorithm: A new bio-inspired metaheuristic algorithm for solving optimization problems[J]. Knowledge-Based Systems,2023,259.



二、多目标浣熊优化算法MOCOA
多目标优化算法:多目标浣熊优化算法(Multi-objective Coati Optimization Algorithm,MOCOA) - 知乎 (zhihu.com)
多目标浣熊优化算法(multi-objective Coati Optimization Algorithm,MOCOA)由COA融合多目标策略而成,为了验证所提的MOCOA的有效性,将其在46个多目标测试函数(ZDT1、ZDT2、ZDT3、ZDT4、ZDT6、DTLZ1-DTLZ7、WFG1-WFG10、UF1-UF10、CF1-CF10、Kursawe、Poloni、Viennet2、Viennet3)以及1个工程应用(盘式制动器设计)上实验,并采IGD,GD,HV,SP四种评价指标进行评价。
部分代码:
close all;
clear ;
clc;
%%
% TestProblem测试问题说明:
%一共46个多目标测试函数(1-46)+5个工程应用(47-50),详情如下:
%1-5:ZDT1、ZDT2、ZDT3、ZDT4、ZDT6
%6-12:DTLZ1-DTLZ7
%13-22:wfg1-wfg10
%23-32:uf1-uf10
%33-42:cf1-cf10
%43-46:Kursawe、Poloni、Viennet2、Viennet3
%47 盘式制动器设计 https://blog.youkuaiyun.com/weixin_46204734/article/details/124051747
%%
TestProblem=1;%1-47
MultiObj = GetFunInfo(TestProblem);
MultiObjFnc=MultiObj.name;%问题名
% Parameters
params.Np = 200; % Population size 种群大小
params.Nr = 200; % Repository size 外部存档中最大数目,可适当调整大小,越大,最终获得的解数目越多
params.maxgen =200; % Maximum number of generations 最大迭代次数
REP = MOCOA(params,MultiObj);
%% 画结果图
figure
if(size(REP.pos_fit,2)==2)
h_rep = plot(REP.pos_fit(:,1),REP.pos_fit(:,2),'ok'); hold on;
if(isfield(MultiObj,'truePF'))
h_pf = plot(MultiObj.truePF(:,1),MultiObj.truePF(:,2),'.r'); hold on;
legend('MOCOA','TruePF');
else
legend('MOCOA');
end
grid on; xlabel('f1'); ylabel('f2');
end
if(size(REP.pos_fit,2)==3)
h_rep = plot3(REP.pos_fit(:,1),REP.pos_fit(:,2),REP.pos_fit(:,3),'ok'); hold on;
if(isfield(MultiObj,'truePF'))
h_pf = plot3(MultiObj.truePF(:,1),MultiObj.truePF(:,2),MultiObj.truePF(:,3),'.r'); hold on;
legend('MOCOA','TruePF');
else
legend('MOCOA');
end
grid on; xlabel('f1'); ylabel('f2'); zlabel('f3');
end
title(MultiObjFnc)
Obtained_Pareto=REP.pos_fit;
if(isfield(MultiObj,'truePF'))%判断是否有参考的PF
True_Pareto=MultiObj.truePF;
%% Metric Value
% ResultData的值分别是IGD、GD、HV、Spacing (HV越大越好,其他指标越小越好)
ResultData=[IGD(Obtained_Pareto,True_Pareto),GD(Obtained_Pareto,True_Pareto),HV(Obtained_Pareto,True_Pareto),Spacing(Obtained_Pareto)];
else
%计算每个算法的Spacing,Spacing越小说明解集分布越均匀
ResultData=Spacing(Obtained_Pareto);%计算的Spacing
end
%%
% Display info
disp('Repository fitness values are stored in REP.pos_fit');
disp('Repository particles positions are store in REP.pos');部分结果:
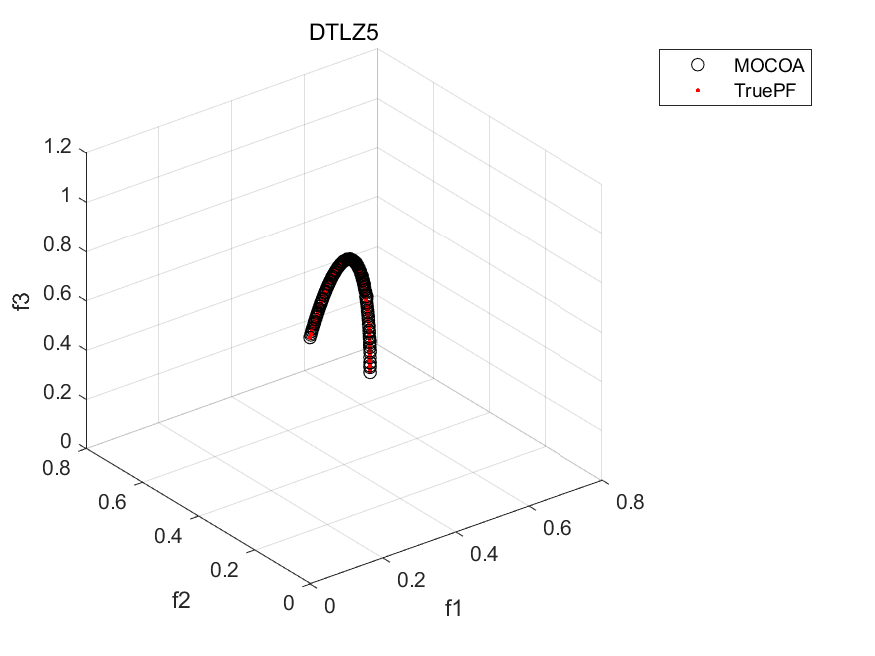

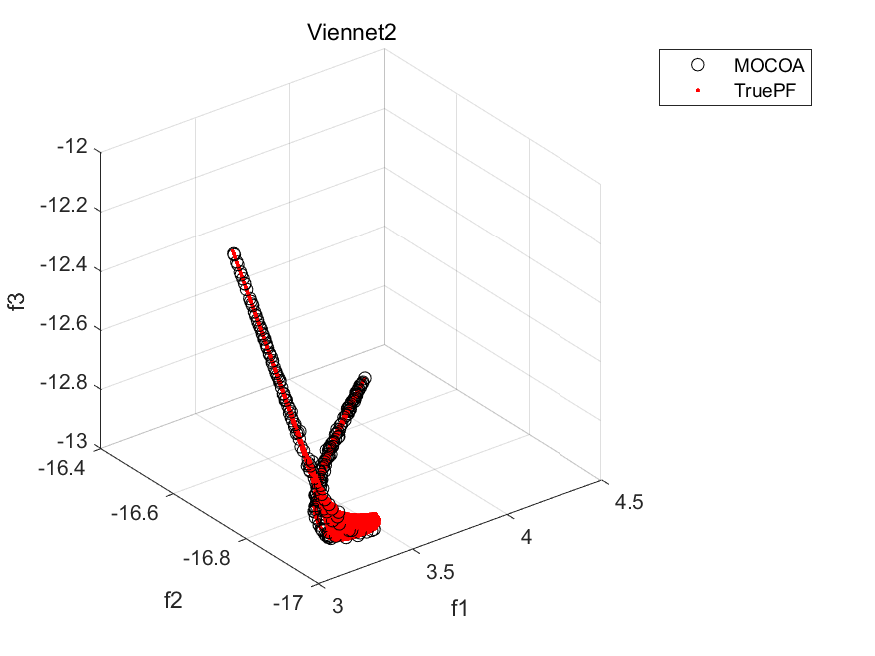






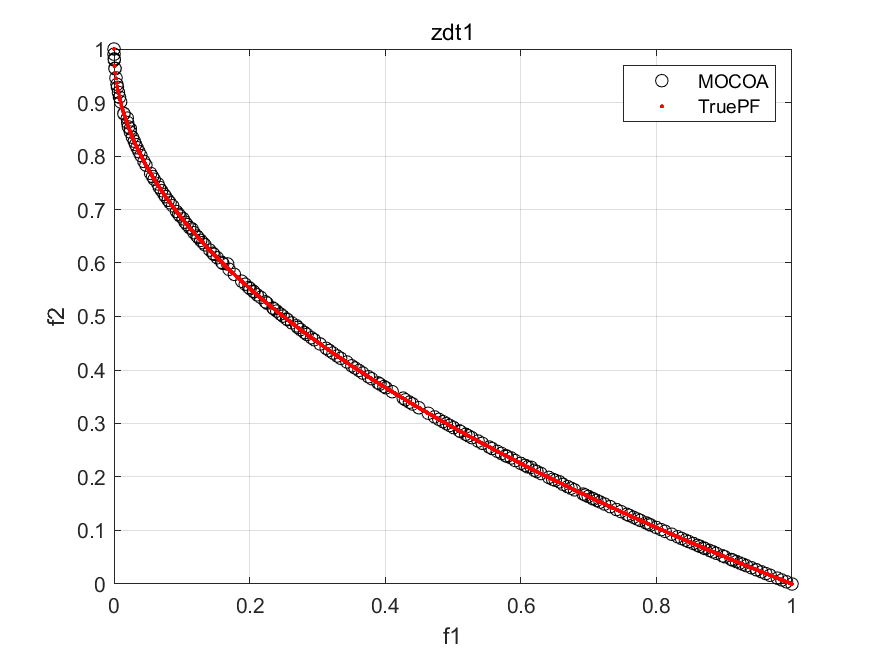










 文章介绍了浣熊优化算法(COA)及其多目标版本MOCOA,COA以其强大的进化能力和快速收敛性在优化问题中展现出优势。MOCOA则扩展到多目标场景,通过在多种测试函数和工程问题上的实验,证明了其有效性和性能。提供的MATLAB代码示例展示了MOCOA的实现过程和结果可视化。
文章介绍了浣熊优化算法(COA)及其多目标版本MOCOA,COA以其强大的进化能力和快速收敛性在优化问题中展现出优势。MOCOA则扩展到多目标场景,通过在多种测试函数和工程问题上的实验,证明了其有效性和性能。提供的MATLAB代码示例展示了MOCOA的实现过程和结果可视化。
















 5608
5608

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








