MATLAB 控制系统设计与仿真

本文链接：https://blog.youkuaiyun.com/weixin_46185665/article/details/145978061

二阶系统的时域分析

一般控制系统均为高阶系统，但在一定准确条件下，可忽略某些次要因素从而近似的用一个二阶系统来表示。

一般研究二阶系统有较大的实际意义。

例如，描述力反馈型电液伺服阀的微分方程一般为四阶，五阶高次方程，但在实际中，电液控制系统通常按二阶系统来分析已经足够准确了。

二阶系统的实例很多，例如RCL电网络，带有惯性载荷的液压助力器，质量弹簧阻尼机械系统。

二阶系统的数学模型

二阶系统是指用二阶微分方程描述的控制系统。其传递函数的一般格式为：

$\Phi(s)=\frac{C(s)}{R(s)}=\frac{K}{Ts^2+Ds+K}$

其中，控制系统的时间常数为T，增益为K，阻尼为D。在控制系统研究领域，为了使研究的结果具有普遍意义，通常将上式改写为标准形式：

$\Phi(s)=\frac{w_n^2}{s^2+2\zeta w_ns+w_n^2}$

其中，系统的阻尼比为 ζ ,固有频率为 $w_n$ ,即自然振荡频率，两个参数之间的关系为：

$w_n=\sqrt{\frac{K}{T}}, \zeta =\frac{D}{2\sqrt{KT}}$

二阶系统的分类

二阶系统的分母就是一个二元一次方程，其特征方程的根为：

$s_{1,2}=-\zeta w_n\pm w_n \sqrt{\zeta ^2 -1}$

根据阻尼比 ζ 的大小情况，对二阶系统进行如下分类:

(1) ζ<0 ,负阻尼系统，系统不稳定

(2) ζ=0 ,零阻尼系统， $s_{1,2}=\pm jw_n$

(3) 0<ζ<1 ,欠阻尼系统， $s_{1,2}=-\zeta w_n\pm jw_n \sqrt{\zeta ^2 -1}$

(4) ζ=1 ,临界尼系统， $s_{1,2}=-w_n$

(5) ζ>1 ,过阻尼系统， $s_{1,2}=-\zeta w_n\pm w_n \sqrt{\zeta ^2 -1}$

欠阻尼系统的性能分析

如果采用单位阶跃输入信号，我们可以推到出二阶欠阻尼系统的解析解，进而我们可以根据各个指标的定义计算出

（1）延迟时间

（2）上升时间

（3）峰值时间

（4）调节时间

（5）最大超调量

二阶欠阻尼系统，单位阶跃信号输入的解析解为：

$y(t)=1-e^{-\zeta w_n}(cos(w_n\sqrt{1-\zeta^2})t+sin(w_n\sqrt{1-\zeta^2})t)$

(如果大家需要推到过程，请留言，我会单独出一篇文章来说明推到过程）

clear all;clc;
tFinal=1;
t=0:0.001:tFinal;
zeta=0.015;
wn=62.8;
w=wn*sqrt(1-zeta^2);
y=1-exp(-zeta*wn*t).*(cos(w*t)-zeta/sqrt(1-zeta^2)*sin(w*t));
plot(t,y);
grid on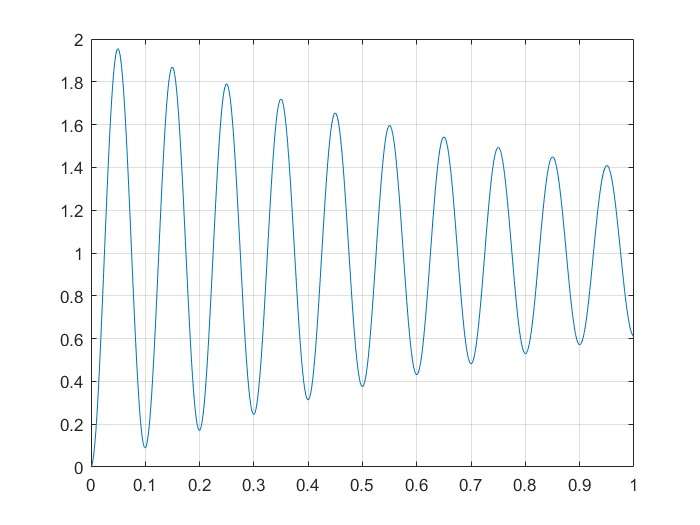

最后，欢迎大家有问题给我留言。

另外欢迎小伙伴们点赞转发加关注。

谢谢大家！！

MATLAB 控制系统设计与仿真 - 10

二阶系统的时域分析