一阶系统的时域分析
一阶系统的微分方程为:
当初始条件为零时,线性系统的传递函数为:
对于不同的典型输入信号,系统的响应是不同的。
1。 一阶系统的单位阶跃响应
由于单位阶跃信号的Laplace变换为 ,则系统的输出为:
对于上式求取Laplace逆变换,可以得到
MATLAB 实例
clear all;clc;
T=0.1;
sys=tf(1,[T 1]);
[y_1 t x]=step(sys,1);
y_2=1-exp(-t/T);
plot(t,y_1,'-b');
hold on
grid on
plot(t,y_2,'o');
legend('y_1','y_2')运行结果为:
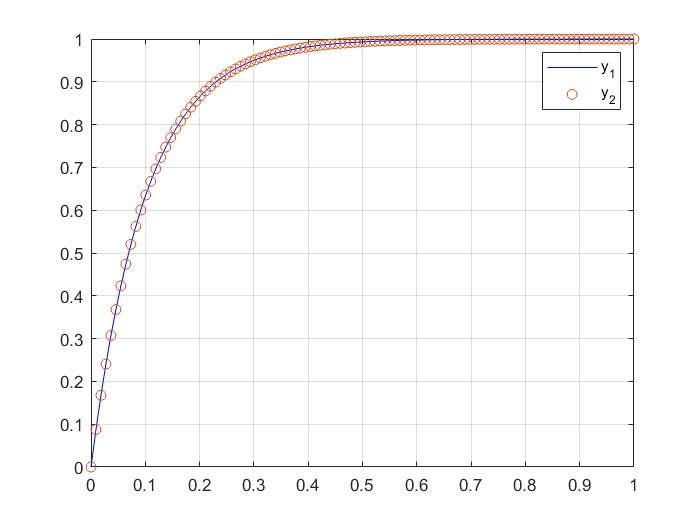
两个方法的出的结构完全一致。
2。 一阶系统的脉冲响应
如果输入为单位脉冲函数,即
所以系统的响应与原来系统的传递函数相同, 即
对上式进行Laplace逆变换可得到系统的单位脉冲响应:
MATLAB 实例
clear all;clc;
T=0.1;
sys=tf(1,[T 1]);
[y_1 t x]=impulse(sys,1);
y_2=1/T*exp(-t/T);
plot(t,y_1,'-b');
hold on
grid on
plot(t,y_2,'o');
legend('y_1','y_2')运行结果为:
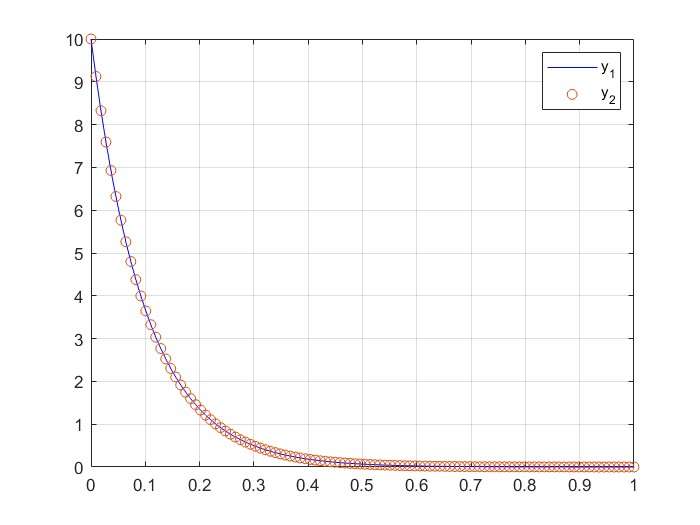
3。同理,我们可以得到一阶系统的单位斜坡响应
clear all;clc;
T=0.1;
sys=tf(1,conv([T 1],[1 0]));
[y_1 t x]=step(sys,1);
y_2=t-T+T*exp(-t/T);
plot(t,y_1,'-b');
hold on
grid on
plot(t,y_2,'o');
legend('y_1','y_2')运行结果为:
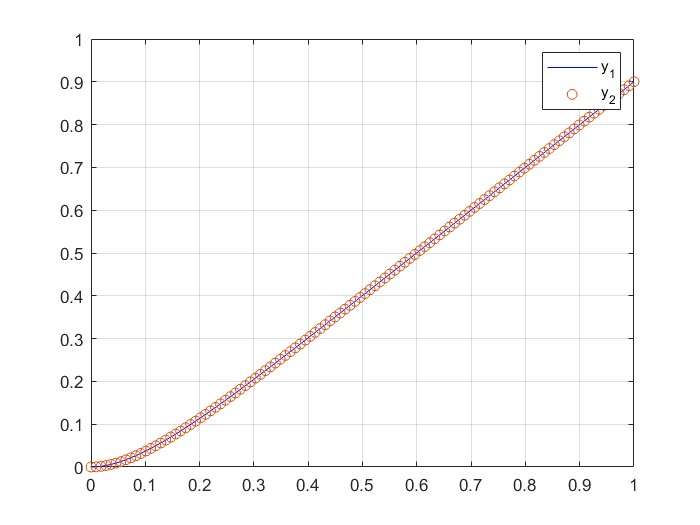
最后,欢迎大家有问题给我留言。
另外欢迎小伙伴们点赞转发加关注。
谢谢大家!!


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










