01背包最小字典序方案（dp）

最新推荐文章于 2024-06-17 18:00:01 发布

原创最新推荐文章于 2024-06-17 18:00:01 发布 · 378 阅读

1 ·

CC 4.0 BY-SA版权

这篇博客讨论了01背包问题的一个变种，即在保证最大价值的同时，求解使得物品选择顺序具有最小字典序的方案。通过动态规划方法，博主详细阐述了如何修改经典01背包算法，以找到剩余容量下能取得的最大价值，并给出了一段C++代码实现这一过程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目链接
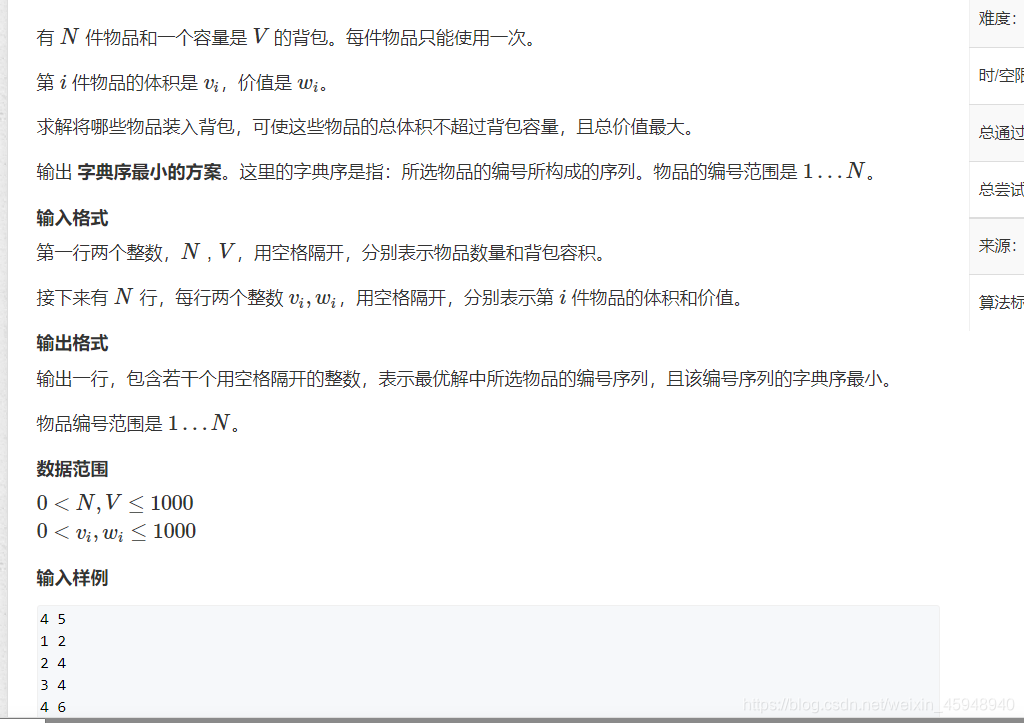
在这里插入图片描述
与01背包相比多了一个输出最小字典序的方案。
原本01背包表示dp[i][j] 前i个数使用了容量为j的背包能获得的最大值
现在来考虑dp[i][j] 对于【i,n】个物品剩余容量为j时候能放的最大价值
dp[i][j]: [i,n]剩余j的最大价值
dp[i+1][j-a[i]] ：取了 i

 #include<bits/stdc++.h>
#include<stdlib.h>
#include<algorithm>
#include<stdio.h>
#include<string.h>
#include<queue>
#include<time.h>
#include <cstdio>
#include <iostream>
#include <vector>
#define ll long long
#define int long long
#define inf 0x3f3f3f3f
#define mods 1000000007
#define modd 998244353
#define PI acos(-1)
#define fi first
#define se second
#define lowbit(x) (x&(-x))
#define mp make_pair
#define pb push_back
#define si size()
#define E exp(1.0)
#define fixed cout.setf(ios::fixed)
#define fixeds(x) setprecision(x)
#define IOS ios::sync_with_stdio(false);cin.tie(0)
 using namespace std;
 ll gcd(ll a,ll b){if(a<0)a=-a;if(b<0)b=-b;return b==0?a:gcd(b,a%b);}
template<typename T>void read(T &res){bool flag=false;char ch;while(!isdigit(ch=getchar()))(ch=='-')&&(flag=true);
for(res=ch-48;isdigit(ch=getchar());res=(res<<1)+(res<<3)+ch - 48);flag&&(res=-res);}
ll lcm(ll a,ll b){return a*b/gcd(a,b);}
ll qp(ll a,ll b,ll mod){ll ans=1;if(b==0){return ans%mod;}while(b){if(b%2==1){b--;ans=ans*a%mod;}a=a*a%mod;b=b/2;}return ans%mod;}//快速幂%
ll qpn(ll a,ll b, ll p){ll ans = 1;a%=p;while(b){if(b&1){ans = (ans*a)%p;--b;}a =(a*a)%p;b >>= 1;}return ans%p;}//逆元   (分子*qp(分母,mod-2,mod))%mod;

ll a[1111];
ll b[1111];
ll dp[1111][1111];
ll v[11111];
signed main()
{

    ll n,m;
    read(n);
    read(m);
    for(int i=1; i<=n; i++)
    {
        read(a[i]);// v
        read(b[i]);
    }
    for(int i=n; i>=1; i--)
    {
        for(int j=0; j<=m; j++)
        {
            dp[i][j]=dp[i+1][j];
            if(j>=a[i])
                dp[i][j]=max(dp[i+1][j-a[i]]+b[i],dp[i][j]);
        }
    }
    // dp[i][j]: [i,n]剩余j的最大价值
    // dp[i+1][j-a[i]]  ：取了 i
    ll le=m;
    for(int i=1; i<=n; i++)
    {

        if(i==n&&le>=a[i])
        {
            printf("%lld",i);
            break;
        }
        if(le<=0)
            break;
        if(le-a[i]>=0&&dp[i][le]==dp[i+1][le-a[i]]+b[i])
        {
            printf("%lld ",i);
            le=le-a[i];
        }

    }

}