力扣刷题 | 二叉树专题

最新推荐文章于 2025-06-01 06:59:08 发布
最新推荐文章于 2025-06-01 06:59:08 发布
阅读量406 收藏
点赞数
分类专栏： 力扣刷题笔记 文章标签： 笔记 力扣 刷题 golang
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/weixin_45904051/article/details/123539282
版权
本文详细解析了15道二叉树相关的算法题目，包括从上到下打印二叉树、计算深度、查找子结构、翻转、计算节点数、判断对称、平衡、子树、左下角节点、合并、搜索、验证、众数、最近公共祖先、插入、删除等操作。通过递归、双队列等方法进行高效实现，涉及二叉搜索树、深度优先搜索、广度优先搜索等概念。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

各自努力，最高处见！加油！

二叉树专题

1、从上到下打印二叉树I

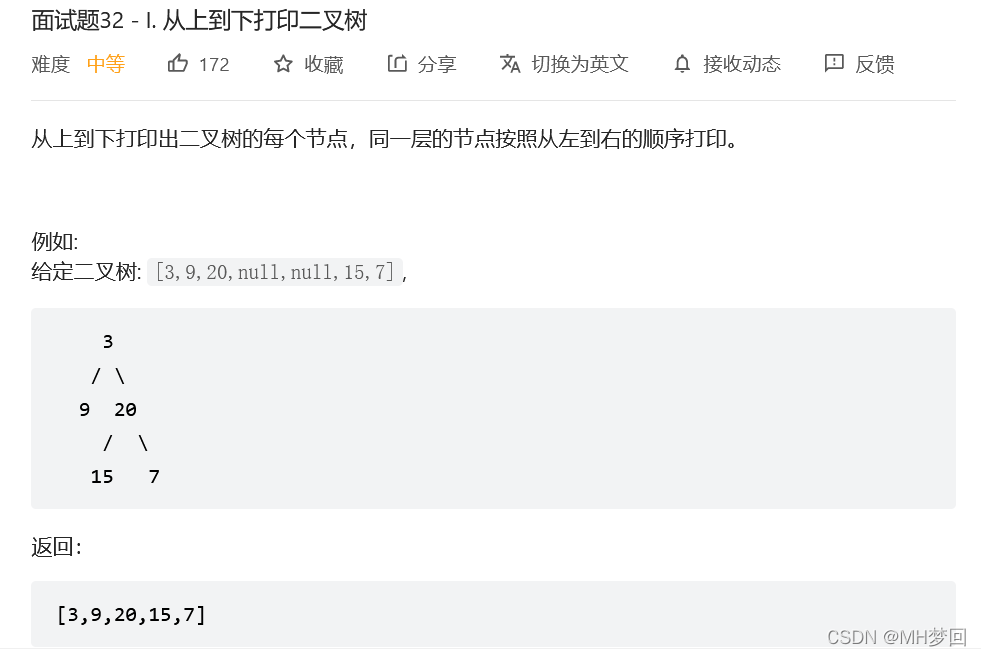
在这里插入图片描述

打印二叉树属于广度优先搜索（BFS）问题，通常用队列来解决问题。go语言中没有官方定义的队列类型，但是可以使用list包来完成队列的功能。
go语言中list的具体操作学习：https://haicoder.net/golang/golang-list.html

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func levelOrder(root *TreeNode) []int {
	result:=make([]int,0)

	if root==nil{
		return result
	}
	que:=list.New()
	que.PushBack(root)
	for que.Len()!=0{
		value := que.Front().Value.(*TreeNode)
		result=append(result,value.Val)
		if value.Left!=nil{
			que.PushBack(value.Left)
		}
		if value.Right!=nil{
			que.PushBack(value.Right)
		}
		que.Remove(que.Front())//更新队头
	}
	
	return result
}

2、 二叉树的深度

在这里插入图片描述

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func maxDepth(root *TreeNode) int {
    count:=0
    arr:=list.New()//存放一层数据
    que:=list.New()
    if root!=nil{
        arr.PushBack(root)
    }else{
        return count
    }
	

	for arr.Len()!=0{
        count++
        //把arr中存的一层数据全部放入队列中
        que.PushBackList(arr)
        arr=list.New()
        for que.Len()!=0{
            value := que.Front().Value.(*TreeNode)
            que.Remove(que.Front())//更新队头
            if value.Left!=nil{
                arr.PushBack(value.Left)
            }
            if value.Right!=nil{
                arr.PushBack(value.Right)
            }
        }

	}
    return count

}

上面方法是利用层序遍历的方法来计算深度，该方法利用了两个队列，消耗的内存很大，需要继续优化。

3、从上到下打印二叉树 II

在这里插入图片描述

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
import "container/list"
func levelOrder(root *TreeNode) [][]int {
    if root==nil{
        return nil
    }
    var array [][]int
    queue:=list.New()
    arr:=list.New()
    arr.PushBack(root)
    var value *TreeNode

    for arr.Len()!=0{
        temp:=make([]int,0)
        for arr.Len()!=0 {
            value = arr.Front().Value.(*TreeNode)
            queue.PushBack(value)
            temp=append(temp,value.Val)
            arr.Remove(arr.Front())//更新队头
        } 
        array=append(array,temp)

        for queue.Len()!=0{
            value=queue.Front().Value.(*TreeNode)
            if value.Left!=nil{
                arr.PushBack(value.Left)
            }
            if value.Right!=nil{
                arr.PushBack(value.Right)
            }
            queue.Remove(queue.Front())
        }
    }
    return array

}

双队列法实现，速度很快，但是消耗内存较多

4、从上到下打印二叉树 III

在这里插入图片描述在这里插入图片描述

多了一步数组的倒序处理，这个方法的运行速度很快，但是内存占比很大，如何优化使用内存？

func levelOrder(root *TreeNode) [][]int {

    queue:=list.New()
    next:=list.New()
    statu:=true
    result:=make([][]int,0)
    if root==nil {
            return nil
    }
    queue.PushBack(root)
    for queue.Len()!=0{
        array:=make([]int,0)
        for queue.Len()!=0{
            var value *TreeNode
            value=queue.Front().Value.(*TreeNode)//取出队头
            queue.Remove(queue.Front())//更新队头
            array=append(array,value.Val)//加入数组中

            if value.Left!=nil{
                next.PushBack(value.Left)
            }
            if value.Right!=nil{
                next.PushBack(value.Right)
            }
        }
        if statu == false {
			l := len(array)
			for i := 0; i < l-1-i; i++ {
				temp := array[l-1-i]
				array[l-1-i] = array[i]
				array[i] = temp
			}
		}
        result=append(result,array)//数组输出
        queue.PushBackList(next)
        next=list.New()
        //转换输出方式
        if statu==true{
            statu=false
        }else{
            statu=true
        }
    }
    return result

}

5、对称的二叉树

在这里插入图片描述

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func isSymmetric(root *TreeNode) bool {
    if root==nil{
        return true
    }
    return recure(root.Left,root.Right)
}
func recure(L,R *TreeNode)bool{
    if L==nil&&R==nil{
        return true
    }
    if L==nil||R==nil||L.Val!=R.Val{
        return false
    }

    f1:=recure(L.Left,R.Right)
    f2:=recure(L.Right,R.Left)

    return f1&&f2
}

递归法
在这里插入图片描述

6、平衡二叉树

在这里插入图片描述
在这里插入图片描述

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func isBalanced(root *TreeNode) bool {
    if recure(root)==-1{
        return false
    }
    return true
}

func recure(root *TreeNode) int {
    if nil==root{
        return 0
    }
    L:=recure(root.Left)
    if L==-1{
        return -1
    }

    R:=recure(root.Right)
    if R==-1{
        return -1
    }

    if L-R<2&&L-R>-2{
        return max(L,R)+1
    }

    return -1
}

func max(a int,b int) int{
    if a>b{
        return a
    }
    return b
}

解题的关键点：如何求解二叉树的深度差

此树的深度 =max(左子树的深度 , 右子树的深度) +1

递归的方法，从底层开始算起，根节点为nil就向上返回0，表示这是第0层。此后每层的计算方法都按照上面的公式计算，逐层递增1，直到根节点。在递归过程中，如果出现一边的返回结果为-1，说明有子树不满足平衡二叉树的要求，直接返回-1.

7、树的子结构

在这里插入图片描述
在这里插入图片描述

回溯法+递归比对
用递归函数查找某节点的树结构跟目标树结构是否一致。
回溯法切换查找的节点。

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func isSubStructure(A *TreeNode, B *TreeNode) bool {
    if B==nil||A==nil{
        return false
    }

    return (recur(A,B)||isSubStructure(A.Left,B)||isSubStructure(A.Right,B))
    // return recur(A,B)//这种写法只是判断根节点开始的树有没有与目标树相同的结构

}

func recur(A *TreeNode, B *TreeNode) bool{//递归结构：如果节点的值相同，判断它的左右子树是否跟目标结构相同
    if B==nil{
        return true//子树的节点为空，说明检索完成，存在完全相同的子结构
    }
    if A==nil||A.Val!=B.Val{
        return false
    }
    return recur(A.Left,B.Left)&&recur(A.Right,B.Right)
}

8、翻转二叉树

在这里插入图片描述

递归解法：递归前序遍历翻转每个节点的左右节点

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func invertTree(root *TreeNode) *TreeNode {
    if root==nil{
        return nil
    }
    //交换左右节点
    temp:=root.Left
    root.Left=root.Right
    root.Right=temp

    invertTree(root.Left)
    invertTree(root.Right)

    return root
}

前序迭代法

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func invertTree(root *TreeNode) *TreeNode {
    if root==nil{
        return nil
    }
    stack:=list.New()
    stack.PushBack(root)
    // stack.PushBack(nil)

    for stack.Len()>0{
        back:=stack.Back().Value
        stack.Remove(stack.Back())
        if back==nil{
            node:=stack.Back().Value.(*TreeNode)
            stack.Remove(stack.Back())
            node.Left,node.Right=node.Right,node.Left
            continue
        }
        node:=back.(*TreeNode)
        if node.Right!=nil{
            stack.PushBack(node.Right)
        }
        if node.Left!=nil{
            stack.PushBack(node.Left)
        }
        stack.PushBack(node)
        stack.PushBack(nil)
    }
    return root

}

9、完全二叉树的节点个数

在这里插入图片描述

层序遍历解法

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func countNodes(root *TreeNode) int {
    //层序遍历
    count:=0
    if root==nil{
        return count
    }
    queue:=list.New()
    queue.PushBack(root)
    count++
    for queue.Len()>0{
        front:=queue.Front().Value.(*TreeNode)
        queue.Remove(queue.Front())
        if front.Left!=nil{
            count++
            queue.PushBack(front.Left)
        }
        if front.Right!=nil{
            count++
            queue.PushBack(front.Right)
        }

    }
    return count

}

完全二叉树递归解法

10、另一棵树的子树

在这里插入图片描述

递归解法
暴力遍历该二叉树的节点，如果发现跟subroot根节点值相同的节点，就以该节点为根节点判断该子树是否与subroot树结构相同。isSub()判断两棵树是否为相同的树。

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func isSubtree(root *TreeNode, subRoot *TreeNode) bool {
    if root==nil&&subRoot==nil{
        return true
    }
    if root==nil||subRoot==nil{
        return false
    }
    if root.Val==subRoot.Val{
        if isSub(root,subRoot){
            return true
        }
    }
    return isSubtree(root.Left,subRoot)||isSubtree(root.Right,subRoot)
}
func isSub(root *TreeNode, subRoot *TreeNode)bool{//
    if root==nil&&subRoot==nil{
        return true
    }
    if root==nil||subRoot==nil||root.Val!=subRoot.Val{
        return false
    }
    return isSub(root.Left,subRoot.Left)&&isSub(root.Right,subRoot.Right)
}

11、找树左下角的值

在这里插入图片描述
递归法
需要搞明白的两个问题：
1、最左边的节点不一定在最底层
2、最底层最左边的节点不一定是左节点
递归解答本题的核心在于

if root.Left==nil&&root.Right==nil{//叶子节点
        if length>maxLength{//只有该层的第一个元素执行这个if语句
            maxLength=length
            leftNode=root.Val
        }
}

扫描到叶子节点就检测该节点所在的层是否大于已经扫描的最大层数，如果大于，就更新全局数据。这个if语句只有在扫描到每一层的第一个节点才会更新，所以就保证了该数据存的是该层的最左节点。

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
var maxLength int
var leftNode int
func findBottomLeftValue(root *TreeNode) int {
    //递归法需要搞明白的两个问题：
    //1、最左边的节点不一定在最底层
    //2、最底层最左边的节点不一定是左节点
    if root.Left==nil&&root.Right==nil{
        return root.Val
    }
    maxLength=0
    leftNode=0
    findLeftLeaves(root,0)
    return leftNode

}
func findLeftLeaves(root *TreeNode,length int){//当前为length层
    if root.Left==nil&&root.Right==nil{//叶子节点
        if length>maxLength{//只有该层的第一个元素执行这个if语句
            maxLength=length
            leftNode=root.Val
        }
    }

    if root.Left!=nil{
        findLeftLeaves(root.Left,length+1)
    }
    if root.Right!=nil{
        findLeftLeaves(root.Right,length+1)
    }
}

12、合并二叉树

在这里插入图片描述

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func mergeTrees(root1 *TreeNode, root2 *TreeNode) *TreeNode {
    if root1==nil&&root2==nil{
        return nil
    }else if root1==nil{
        return root2
    }else if root2==nil{
        return root1
    }
    // root:=&TreeNode{
    //     Val:root2.Val+root1.Val,
    //     Left:mergeTrees(root1.Left,root2.Left),
    //     Right:mergeTrees(root1.Right,root2.Right),
    // }
    root1.Val+=root2.Val
    root1.Left=mergeTrees(root1.Left,root2.Left)
    root1.Right=mergeTrees(root1.Right,root2.Right)
    //递归是从最底层回溯，所以可以更改root1节点
    
    return root1
}

13、二叉搜索树中的搜索

在这里插入图片描述

循环解法

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func searchBST(root *TreeNode, val int) *TreeNode {
    
    for {
        if root==nil{
            return nil
        }else if root.Val==val{
            return root
        }
        if root.Val>val{
            root=root.Left
        }else{
            root=root.Right
        }
        
    }
}

递归解法

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func searchBST(root *TreeNode, val int) *TreeNode {
    if root==nil{
        return nil
    }
    if root.Val==val{
        return root
    }
    if root.Val<val{
        return searchBST(root.Right,val)
    }else{
        return searchBST(root.Left,val)
    }
}

14、验证二叉搜索树

在这里插入图片描述

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
var isBST func(node *TreeNode) bool
func isValidBST(root *TreeNode) bool {
	var pre *TreeNode = nil

	isBST = func(root *TreeNode) bool {
		if root == nil {
			return true
		}
		left := isBST(root.Left)

		if pre != nil && pre.Val >= root.Val {
			return false
		}
		pre = root

		right := isBST(root.Right)

		return left && right
	}

	return isBST(root)

}

15、二叉搜索树中的众数

在这里插入图片描述
递归解法:
判断截止该节点，相同值的节点数量是否大于maxCount，如果大于则更新maxCount并清空数组的数据。

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
var searchBST func(*TreeNode)
func findMode(root *TreeNode) []int {
    res:=make([]int,0)
    if root.Left==nil&&root.Right==nil{//only one
        res=append(res,root.Val)
        return res
    }
    var pre *TreeNode
    maxCount:=0
    count:=0
    searchBST=func(root *TreeNode){
        if root==nil{
            return 
        }
        searchBST(root.Left)
        if pre==nil{
            count=1
        }else if pre!=nil{
            if pre.Val==root.Val{
                count++
            }else{
                
                count=1//重新计数
            }
            
        }
        pre=root
        if count>maxCount{//计算到本节点为止众数的数量是否超过maxCount
            res=make([]int,0)
            res=append(res,pre.Val)
            maxCount=count
        }else if count==maxCount{
            res=append(res,pre.Val)
        }
        searchBST(root.Right)
    }
    searchBST(root)
    return res


}

16、二叉树的最近公共祖先

在这里插入图片描述如果找到一个节点，发现左子树出现结点p，右子树出现节点q，或者 左子树出现结点q，右子树出现节点p，那么该节点就是节点p和q的最近公共祖先。(摘自代码随想录)这道题有一个点是，即使两个pq两个节点都在根节点的左子树，其右子树一样也会遍历，只不过返回的是nil。如在本题例子中（上图），p为jiedian4，q为节点5，公共祖先为5.采用如下递归法遍历到5时便向上一层返回该节点。而1节点返回nil，这时程序就可以判定5就是公共祖先。

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
     if root==nil||root==p||root==q{
         return root
     }


     left:=lowestCommonAncestor(root.Left,p,q)
     right:=lowestCommonAncestor(root.Right,p,q)
     if left!=nil&&right!=nil{
         return root
     }else if left==nil&&right!=nil{
        return right
     }else if left!=nil&&right==nil{
         return left
     }else{
         return nil
     }
}

17、二叉搜索树中的插入操作

在这里插入图片描述

递归解法
我写的代码如下，我的思路是只有当val所在的方向为空时，才接受返回值，但是其实这一步完全可以省略。因为这是在递归中，在递归回溯的时候，左子节点或右子节点会赋值到原来的位置。见改进写法（参考代码随想录）。

func insertIntoBST(root *TreeNode, val int) *TreeNode {
    if root==nil{
        root=&TreeNode{
            Val:val,
            Left:nil,
            Right:nil,
        }
    }
    if val<root.Val&&root.Left!=nil{
        insertIntoBST(root.Left,val)
    }else if val>root.Val&&root.Right!=nil{
        insertIntoBST(root.Right,val)
    }else if val<root.Val&&root.Left==nil{
        root.Left=insertIntoBST(root.Left,val)
    }else if val>root.Val&&root.Right==nil{
        root.Right=insertIntoBST(root.Right,val)
    }
    return root
}

改进写法

func insertIntoBST(root *TreeNode, val int) *TreeNode {
    if root==nil{
        root=&TreeNode{
            Val:val,
            Left:nil,
            Right:nil,
        }
    }
    if val<root.Val{
        root.Left=insertIntoBST(root.Left,val)
    }else if val>root.Val{
        root.Right=insertIntoBST(root.Right,val)
    }
    return root
}

18、删除二叉搜索树中的节点

在这里插入图片描述

递归法分情况讨论：代码随想录yyds

  • 第一种情况：没找到删除的节点，遍历到空节点直接返回了

  • 找到删除的节点

  1. 第二种情况：左右孩子都为空（叶子节点），直接删除节点， 返回NULL为根节点

  2. 第三种情况：删除节点的左孩子为空，右孩子不为空，删除节点，右孩子补位，返回右孩子为根节点

  3. 第四种情况：删除节点的右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点

  4. 第五种情况：左右孩子节点都不为空，则将删除节点的左子树头结点（左孩子）放到删除节点的右子树的最左面节点的左孩子上，返回删除节点右孩子为新的根节点。

func deleteNode(root *TreeNode, key int) *TreeNode {
    if root==nil{
        return nil
    }
    if root.Val==key{//找到删除的节点
        if root.Left==nil&&root.Right==nil{
            return nil
        }
        if root.Left==nil&&root.Right!=nil{
            return root.Right
        }
        if root.Right==nil&&root.Left!=nil{
            return root.Left
        }
        if root.Right!=nil&&root.Left!=nil{
            ptr:=root.Right
            for ptr.Left!=nil{
                ptr=ptr.Left
            }
            ptr.Left=root.Left
            return root.Right
        }
    }
    //没找到要删除的节点
    root.Left=deleteNode(root.Left,key)
    root.Right=deleteNode(root.Right,key)
    return root
    
}

19、将有序数组转换为二叉搜索树(递归+二分思想)

在这里插入图片描述

func sortedArrayToBST(nums []int) *TreeNode {
    return traversal(nums,0,len(nums)-1)
}
func traversal(nums []int,left int,right int)*TreeNode{
    if left>right{
        return nil
    }
    mid:=left+(right-left)/2
    root:=&TreeNode{
        Val:nums[mid],
        Left:traversal(nums,left,mid-1),
        Right:traversal(nums,mid+1,right),
    }
    return root
}

经验：

力扣runtime: out of memory: cannot allocate 4194304-byte block (469499904 in use

出现这种错误先检查代码中是否存在死循环，可能是循环的条件有错或者for循环的 i 变量没有递增导致的。

如何计算树的最大深度

func maxdepth(root *TreeNode)int{
    if root==nil{
        return 0
    }
    return max(maxdepth(root.Left),maxdepth(root.Right))+1
}
func max(a,b int)int{
    if a>b{
        return a
    }
    return b
}

递归法什么时候有返回值？

如果需要遍历整棵树，递归函数就不能有返回值。如果需要遍历某一条固定路线，递归函数就一定要有返回值！

本专栏所有力扣题目的目录链接, 刷算法题目的顺序(由易到难/面试频率)/注意点/技巧, 以及思维导图源文件问题(持续更新中)
孤柒的博客
05-14 1万+
这篇文章为本专栏所有力扣题目提供目录链接,更加方便读者根据题型或面试频率进行阅读,此外也会介绍我在刷题过程中总结的刷算法题目的顺序/注意点/技巧,最后说下文中出现的思维导图源文件的问题. 我主页中的思维导图中内容大多从我的笔记中整理而来,相应技巧可在笔记中查找原题, 有兴趣的可以去 我的主页了解更多计算机学科的精品思维导图整理 本文可以转载，但请注明来处，觉得整理的不错的小伙伴可以点赞关注支持一下哦！ 博客中思维导图的高清PDF版本,可关注公众号 一起学计算机 点击 资源获取 获得 一.所...
Python 刷题笔记：二叉树专题一
TEDxPY
05-11 657
今天来看二叉树专题，首先我们先整理下关于二叉树的基础知识点；基于在 LeetCode 推荐题解中发现了一个适用于二叉树遍历的套路解法，我们今天也会连刷三道关于前序、中序和后序遍历的 LeetCode 题目。 这个改变对二叉树认知的神奇解法，真的非常值得一看！ 基础知识点 树 首先看下“树”的概念： 树是一种抽象数据类型（ADT）或是实现这种抽象数据类型的数据结构，用来模拟具有树状结构性质的数据集合。它是由 n(n>0) 个有限节点组成一个具有层次关系的集合。 链接：https://leetcode-
力扣刷题之准备工作
weixin_47040031的博客
05-01 4872
在刷算法题的过程中进行总结是非常重要的，它可以帮助你梳理思路、加深理解、记录学习成果，并提升解题能力。每天回顾：在每天结束时，对当天解决的题目进行回顾。检查解决方案的正确性，并思考是否有更优化的方法。记录下遇到的难点和解决方法，以及学到的新知识点和技巧。整理这些笔记并归档到适当的分类中，以便今后参考。每周汇总：在每周末或开始新一周时进行总结。复习过去一周解决的题目，分析解题过程中使用的算法和数据结构。总结你学到的关键知识点、解题技巧和模式，并将其整理到博客中。
【力扣刷题】Day17——二叉树专题
涛涛的个人博客
10-07 410
【力扣刷题】Day17——二叉树专题
【力扣刷题】Day14——二叉树专题
涛涛的个人博客
10-05 752
【力扣刷题】Day14——二叉树专题
力扣刷题路线
FAQEW的博客
03-27 1057
结合高频题、经典题和算法思想学习建议，分阶段从基础到进阶编排，覆盖所有核心标签，并标注题号与学习方法。：画图模拟快慢指针移动，如移动零时快指针探路、慢指针标记非零位置。：括号生成时，左括号数不能超过n，右括号数不能超过左括号数。：LCA问题中，若左右子树均含目标节点，则当前节点为祖先。：终止条件、递归调用、返回值，如二叉树深度递归返回。：掌握虚拟头节点、递归反转、环形检测。：掌握索引操作、快慢指针、滑动窗口。：熟悉括号匹配、单调栈、层序遍历。：熟悉反转、哈希统计、回文处理。
【力扣刷题】Day18——二叉树专题
涛涛的个人博客
10-08 634
【力扣刷题】Day18——二叉树专题
【力扣刷题】Day16——二叉树专题
涛涛的个人博客
10-06 766
【力扣刷题】Day16——二叉树专题
【力扣刷题】Day20——二叉树专题
涛涛的个人博客
10-10 944
【力扣刷题】Day20——二叉树专题
【力扣刷题】Day15——二叉树专题
涛涛的个人博客
10-05 883
【力扣刷题】Day15——二叉树专题
【力扣刷题】Day21——二叉树专题
涛涛的个人博客
10-11 595
【力扣刷题】Day21——二叉树专题
leetcode力扣刷题攻略路线推荐
02-15
### LeetCode 力扣 刷题 攻略 学习 路线 推荐 #### 合理规划学习路径 对于初学者而言，在LeetCode上盲目地从头开始做题并不是最优策略，因为这可能导致早期遇到困难而失去信心。合理的刷题攻略应该遵循由易至难的...
Leetcode-How-What 力扣Leetcode刷题指南
edwardwjz的博客
03-05 3296
Leetcode-How-What 力扣Leetcode刷题指南 About the way how to use Leetcode wisely for preparing the interview and the solutions to some Leetcode problems’. 怎样为准备面试机智聪明的刷题（高效刷题）以及一些题目的题解。 同 github 链接： https:/...
力扣树专题-3 树的重建 leetcode105 106 Java刷题笔记
一碗菜粥的博客
05-31 330
两道很像的题~通过中序 + 后序 或者 中序 + 前序 来进行二叉树的重建
uni-app学习笔记十五-vue3页面生命周期(二)
shenxiaomo1688的博客
05-28 550
onShow：用于监听页面显示，页面每次出现在屏幕上都触发，包括从下级页面点返回露出当前页面；onHide:监听页面隐藏，当离开当前页面时触发。
学习笔记：3个学习AI路上反复看到的概念：RAG，Langchain，Agent
FBeetle的博客
05-31 272
RAG的能力核心是有效结合了检索和生成两种方法。基本思路是把私有数据进行切片，向量化后通过向量检索进行召回，再作为上下文输入到通用大模型，模型再进行分析和回答。同时，AI Agent也可以利用RAG技术来提高其在特定任务（如问答或对话系统）中的性能，尤其是在需要外部知识来支持决策时。RAG可以作为LangChain（如果它是一个语言处理工具）的一部分，用于提供更加丰富和准确的语言生成能力。AI Agent可能使用LangChain来处理自然语言的任务，比如理解用户输入和生成响应。
pikachu靶场通关笔记07 XSS关卡03-存储型XSS
mooyuan的网络安全博客
05-29 813
本系列为通过《pikachu靶场通关笔记》的XSS关卡(共10关）渗透集合，通过对XSS关卡源码的代码审计找到XSS风险的真实原因，讲解XSS的原理并进行渗透实践，本文为XSS关卡03-存储型XSS的渗透部分。
【C语言极简自学笔记】项目开发——扫雷游戏
LQYYDSY的博客
05-29 559
本次项目旨在使用 C 语言开发一个控制台版本的扫雷游戏，实现以下基本功能： 初始化游戏棋盘，包括雷区的布置和非雷区域周围雷数的计算。 玩家通过输入坐标来翻开棋盘格子，若翻开雷则游戏失败，若翻开所有非雷格子则游戏胜利。 提供标记雷的功能，方便玩家识别可能有雷的区域。 具备良好的用户交互界面，显示棋盘状态和游戏提示信息。
SAP学习笔记 - 开发17 - 前端Fiori开发 Component 配置（组件化）
最新发布
shi_ly的专栏
06-01 529
本章讲 Component 配置（组件化），其本质就是把一些共通处理给拿出来放到 Component.js 里面。这样做就会缩减Controller.js 里面的代码。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值