Lesson 5.3 ROC-AUC 的计算方法、基本原理与核心特性

原创

已于 2024-11-30 18:31:32 修改 · 1.8k 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#python #人工智能

于 2023-02-05 17:21:02 首次发布

文章详细介绍了ROC曲线和AUC值的概念及其关系，包括ROC曲线的绘制方法、AUC值的计算以及它们的基本性质。通过实例展示了ROC曲线的绘制过程，解释了AUC值如何反映模型分类性能，并与F1-Score进行了对比。ROC曲线的类别对称性和概率敏感性是其重要特性，适合评估模型在偏态数据上的表现。

文章目录

一、ROC 曲线与 AUC 值
- 1. ROC 曲线绘制方法与 AUC 值计算方法
- 2. ROC-AUC 基本性质

接下来，我们进一步讨论关于ROC曲线AUC值的相关内容。

# 科学计算模块
import numpy as np

# 绘图模块
import matplotlib as mpl
import matplotlib.pyplot as plt

# 自定义模块
from ML_basic_function import *

一、ROC 曲线与 AUC 值

1. ROC 曲线绘制方法与 AUC 值计算方法

除了 F1-Score 以外，还有一类指标也可以很好的评估模型整体分类效力，即 ROC 曲线与 AUC 值。
当然这二者其实是一一对应的，ROC（全称为Receiver operating characteristic，意为受试者特征曲线）是一个二维平面空间中一条曲线，而 AUC 则是曲线下方面积（Area Under Curve）的计算结果，是一个具体的值，例如下图所示：

其实 ROC 和 AUC 是一一对应的，因此二者其实是同一个评估指标。
ROC 曲线同样也是基于混淆矩阵衍生的二级指标来进行构建，该指标的计算有些类似于交叉熵的计算过程，会纳入分类模型的分类概率来进行模型性能的评估。
例如此前所说，对正例样本概率越大、负例样本概率越小，则模型性能越好。
ROC 曲线绘制与 AUC 面积计算
接下来，我们来讨论 ROC 曲线的绘制过程。首先，假设逻辑回归对某一组数据分类结果如下，我们按照预测概率从大到小进行排序：

107

数据总共 20 条样本，11 条 1 类样本、9 条 0 类样本。
此时，我们从 1 开始逐渐降低阈值。
在阈值取值范围为 0.9-1 之间时，模型将判别所有样本都属于 0 类，对于上述数据集来说，有混淆矩阵计算结果如下：

此时，我们令 FDR 为平面坐标的横坐标点、TPR 作为平面坐标的纵坐标点，就可以绘制出 ROC 曲线上的第一个点：(0, 0) 点。
当然，从此结果上仍然看不出其模型评估价值，为了绘制 ROC 曲线，我们还需要进一步调整阈值。
此时我们不断降低阈值，当阈值跨过 0.9 时，即介于 0.8 和 0.9 之间时，上述混淆矩阵计算结果将发生变化，此时模型将判别概率为 0.9 的样本为 1 类，其余样本为 0 类，此时上述混淆矩阵计算结果如下：

而此时我们就计算出了 ROC 曲线上的第二个点：(0, 0.09)。
如果我们进一步降低阈值，当阈值移动到 0.7 和 0.8 之间时，模型判别结果又将发生变化，我们可以继续计算此时的 TPR 和 FDR。
在不断调整阈值的过程中，阈值每跨越一个样本的预测概率，FDR 和 TPR 就会发生变化，最终，我们将阈值从 1 逐渐降低到 0 的过程中的所有计算结果放在数据表中进行观察:

当然，我们也可以简单验证上述结果是否正确。例如，当阈值取值范围在 0.4-0.51 之间时，有一半样本被预测 1、另一半被预测为 0，此时混淆矩阵计算结果为：

在这里插入图片描述

能够发现与表格中结果计算结果一致。
当然，FPR 和 TPR 计算结果还有另一个理解角度，那就是我们可以将 FPR 计算结果视作 0 类概率累计结果，TPR 视作 1 类概率累计结果。
对于上述数据，1 类数据共有 11 条，0 类数据共有 9 条，假设当阈值移动到某个位置时，阈值以上总共有 m 条 1 类样本、n 条 0 类样本，则此时 FPR=n/9，TPR=m/11。
例如当阈值移动到 0.6-0.7 之间时，m=2、n=1，此时 FPR=1/9=1.1，TPR=2/18。
当阈值完整从 1 移动 0 之后，我们即可把上述所有由 (FPR,TPR) 所组成的点绘制成一张折线图，该折线图就是 ROC 曲线图：

在这里插入图片描述

而此时，ROC 曲线下方面积就是 AUC 值。
根据上述描述，FPR 实际上是 0 类概率累计，TPR 实际上是 1 类概率累计，则自上而下观察 True Class 这一列，在原点为起始点时，每当出现一个 1 时，点就沿着 Y 轴正方向移动 0.9，每当出现一个 0 时，点就沿着 X 轴正方向移动 0.11，依次类推，最终从原点移动到 (1,1) 这个点的过程，就构成了 ROC 曲线。

2. ROC-AUC 基本性质

首先，由于 FPR 和 TPR 都是在 [0,1] 区间范围内取值，因此 ROC 曲线上的点分布在横纵坐标都在 [0,1] 范围内的二维平面区间内。
其次，对于任意模型来说，ROC 曲线越靠近左上方、ROC 曲线下方面积越大，则模型分类性能越好。
根据点的移动轨迹构成 ROC 曲线角度来理解，刚开始移动时，是朝向 X 还是 Y 轴正向移动，其实是有模型输出概率最高的几个样本决定的，如果这几个样本被判别错了（即实际样本类别为 0），则刚开始从原点移动就将朝着X轴正方向移动，此时曲线下方面积会相对更小（相比刚开始朝着Y轴正方向移动的情况）。
根据此前介绍的理论，此时由于模型对于“非常肯定”的样本都判错了，证明模型本身判别性能欠佳；而反之，如果输出概率最高的头部几条样本都判断正确，样本真实类别确实属于 1，则点开始移动时将朝向 Y 轴正方向移动，此时曲线下方面积就将相对更大，模型判别性能也将相对较好。此处可以举例说明：

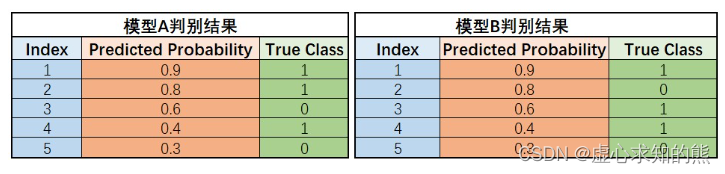
在这里插入图片描述

上述两个模型对于同一组数据的建模结果差异，可以简单看成模型 A 中概率结果为 0.8 和 0.6 的两条样本，在模型 B 中被识别为 0.6 和 0.8，两条样本结果互换。
例如，在 0.5 为阈值的情况下，模型 A 和 B 同样准确率是 80%，但模型 A 是将概率为 0.6 的 1 类样本误判为 0 类、将概率为 0.4 的样本误判为 1 类，尚且有情可原，毕竟 0.6 和 0.4 的模型输出结果代表着模型其实并没有对这两类样本的所属情况有非常强的肯定。
但对于模型 B 来说，有一条概率结果为 0.8 的样本被误判，则说明模型 B 对于一条“非常肯定”属于 1 类的样本判断是错误的，B 模型的“错误”更加“严重”，模型判别性能相对较弱，ROC 曲线下方面积相对较小。
我们可以在 ROC 曲线上能够进行非常清楚的展示，接下来就可以通过代码实现上述两个模型的 ROC 曲线绘制：
从这个角度来看，ROC-AUC 对模型的分类性能评估和交叉熵计算结果类似。

# 定义阈值取值范围
thr_l = np.linspace(1, 0, 100)

# 输入两个模型预测结果和数据真实标签
yhat_A = np.array([0.9, 0.8, 0.6, 0.4, 0.3]).reshape(-1, 1)
y_A = np.array([1, 1, 0, 1, 0]).reshape(-1, 1)
yhat_B = np.array([0.9, 0.8, 0.6, 0.4, 0.3]).reshape(-1, 1)
y_B = np.array([1, 0, 1, 1, 0]).reshape(-1, 1)

# TPR计算过程
y_cla = logit_cla(yhat_A, thr=0.5)
P = y_cla[y_A == 1]
TPR = P.mean()
TPR
#0.6666666666666666

logit_cla(yhat_A, thr=0.5)
#array([[1.],
#       [1.],
#       [1.],
#       [0.],
#       [0.]])

y_A
#array([[1],
#       [1],
#       [0],
#       [1],
3       [0]])

[y_A == 1]
#[array([[ True],
#        [ True],
#        [False],
#        [ True],
#        [False]])]

logit_cla(yhat_A, thr=0.5)[y_A == 1].mean()
#0.6666666666666666

# FPR计算过程
N = y_cla[y_A == 0]
FPR = N.mean()
FPR
#0.5

y_cla = logit_cla(yhat_A, thr=0.5)
y_cla
#array([[1.],
#       [1.],
#       [1.],
#       [0.],
#       [0.]])

y_A
#array([[1],
#       [1],
#       [0],
#       [1],
#       [0]])

[y_A == 0]
#[array([[False],
#        [False],