ROC-AUC 与 PR-AUC 的区别与联系

最新推荐文章于 2024-05-19 19:34:38 发布

笑傲NLP江湖

最新推荐文章于 2024-05-19 19:34:38 发布

阅读量1.2k

点赞数

本文链接：https://blog.youkuaiyun.com/KaikebaAI/article/details/119417039

版权

ROC-AUC 和 PR-AUC 是评估分类模型性能的指标。ROC-AUC 关注模型对正负样本的排序能力，不受数据不平衡影响，而 PR-AUC 更适用于数据不平衡场景，强调正样本的识别能力。两者计算涉及真正例率(TPR)、假正例率(FPR)、精确度(Precision)和召回率(Recall)。在评估时，ROC-AUC 更关注整体性能，PR-AUC 更侧重正样本的性能提升。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

相关术语解释：

	正例	负例
预测正	真正例 (true positive, TP)	假正例 (false positive, FP)
预测负	假负例 (false negative, FN)	真负例 (true negative, TN)

真正例率 (true positive ratio) ： $TPR=\frac{TP}{TP+FN}$ ，表示的是所有正例中被预测为正例的比例
假正例率 (false positive ratio)： $FPR=\frac{FP}{FP+TN}$ ，表示所有负例中被错误地预测为正例的比例
精确度 (precision)： $P=\frac{TP}{TP+FP}$ ，表示所有预测为正的样本中真正为正样本的比例
召回率 (recall)： $R=\frac{TP}{TP+FN}$ ，表示的是所有正例中被预测为正例的比例

其中，真正例率等于召回率

ROC-AUC 与 PR-AUC

定义及计算

ROC，Receiver Operation Characteristics

AUC，Area Under Curve

ROC-AUC 指的是 ROC 曲线下的面积

通过在 [0, 1] 范围内选取阈值 (threshold) 来计算对应的 TPR 和 FPR，最终将所有点连起来构成 ROC 曲线。

一个没有任何分类能力的模型，意味着 TPR 和 FPR 将会相等 (所有正例将会有一半被预测为正例，所有负例也将会有一半被预测为正例)，这时 ROC 曲线将会如下图蓝色虚线所示。

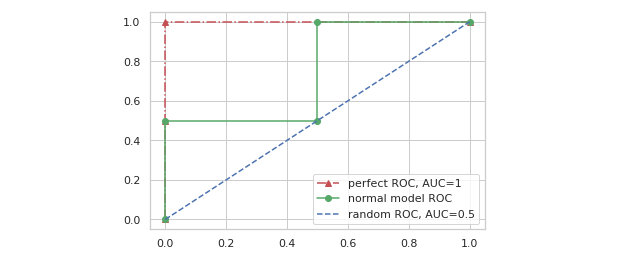
那么在 ROC-AUC 的衡量下，一个理想模型的输出应该是怎样的呢？可以从 TPR 和 FPR 的定义出发，我们肯定是希望理想中的模型在面对正样本时预测为正的概率一定比面对负样本时预测为正的概率大，假设有样本标签和模型预测概率如下：

y = np.array([0, 0, 1, 1])
pred = np.array([0.1, 0.4, 0.45, 0.8])

现在分别选择 5 个阈值 0，0.3，0.42，0.6，1，TPR 和 FPR 如下：

阈值等于 0 时：

$TP=2,\quad TN=0,\quad FP=2,\quad FN=0 \\ TPR=\frac{2}{2+0}=1 \\ FPR=\frac{2}{2+0}=1$

阈值等于 0.3 时：
$TP=2,\quad TN=1,\quad FP=1,\quad FN=0 \\ TPR=\frac{2}{2+0}=1 \\ FPR=\frac{1}{1+1}=0.5$

最低0.47元/天解锁文章