#赛前快速过一遍基础和提高的动态规划课（持续更新）

最新推荐文章于 2025-06-13 14:09:45 发布

欧阳小百合

最新推荐文章于 2025-06-13 14:09:45 发布

阅读量186

点赞数 1

分类专栏： acwing 文章标签：动态规划算法

本文链接：https://blog.youkuaiyun.com/weixin_45849398/article/details/120993879

版权

acwing 专栏收录该内容

1 篇文章

订阅专栏

动态规划

Y总，唯一一个心甘情愿让我为他花钱的男人。

时间复杂度：状态数量*转移计算次数。

常用模型背包

$n$ 个物品，容量为 $v$ 的背包，每个物品有价值 $v_i$ 和重量 $w_i$ 。

01背包：每个物品就一个，只有有或没有两个状态。
完全背包：每个物品无限个。
多重背包：每个物品有限个，最多 $s_i$ 个。
分组背包：每组里最多选1个物品，物品间可能有互斥关系。

在背包容量内寻找符合条件的取法。

状态表示：几维分别表示什么；
表示的集合是什么。
条件和所有选法。
集合的属性是什么。
属性可以考虑 $m i n, m a x, n u m$ 。
从集合角度理解Dp。
状态计算：和状态怎么递推。
对应集合划分，保证不重不漏！
Dp优化：对代码和计算方式等价变形

01背包里面就是把集合划分为两大类，选法包含第i个物品，不包含第i个物品。
dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+w[i]);
考虑j-w[i]是否合法
转化为一维。
在这里插入图片描述
要从大往小枚举j，不然就是用这个划分来更新同一个划分，因为j-v[i]肯定先更新，那每次都是j-v[i]再搞了。反正模拟一下就懂了。所以j要从大往小。
要求算dp[j]的时候，dp[j-v[i]]还没被算过。

滚动数组：
如果这一层更新只用到了上一层，只要开两层就行。滚动交替来算。

完全背包
在这里插入图片描述
对不起Y总。

递推：第i个物品选了多少个，最多到剩余容量个。
代码第一代就是朴素三重循环：

    for (int i = 1; i <= n; i++)
        for (int j = 0; j < m; j++) {
            for (int k = 0; k * v[i] <= j; k++)
                dp[i][j] = max(dp[i][j], dp[i - 1][j - k * v[i]] + k * w[i]);
        }

![在这里插入图片描述](https://img-blog.csdnimg.cn/6a73a60dbc79452b9ef71b9759631246.png?x-oss-process=image/watermark,type_ZHJvaWRzYW5zZmFsbGJhY2s,shadow_50,text_Q1NETiBA5qyn6Ziz5bCP55m-5ZCI,size_20,color_FFFFFF,t_70,g_se,x_16

滚动数组惊奇优化。
在这里插入图片描述
时间复杂度小了5倍。
那就和01背包很像了，区别在于：

01背包都是 $i - 1$ 层转过来
完全背包是 $i - 1 a n d i$ 层转过来。
因为01背包涉及到上个物品和下个物品的转化，这个物品的状态是上一个推过来的；完全背包则是这个物品选了几个以及上一个物品状态结合起来转移的。

多重背包
dp[i][j]=max(dp[i-1][j-v[i]*k]+w[i]*k);
k=0,1,2,3..s[i];

在这里插入图片描述
参考完全背包优化，选中部分可以转移，但是多了一坨…
分组为1，2，4，8…512，理论上通过每一个的选与不选得出所有组合方案。
其中一维变成log。
二进制优化！

最后一个不用要满二进制，sum==s。
等于里面叠了个01背包，选与不选。
复杂度变成nvlogs。
在这里插入图片描述

分组背包
dp[j]=max(dp[j],dp[j-v[i][k];
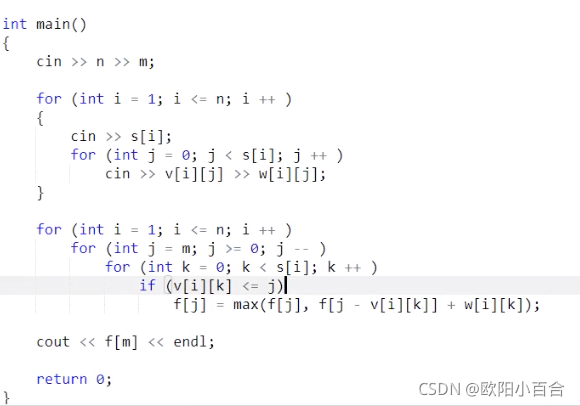
在这里插入图片描述
选这一组和不选的转移。

例题

题目传送门

定义 $dp_{i,j}$ =前 $i$ 个物品，体积不超过 $j$ 的最大价值。

#include<bits/stdc++.h>

using namespace std;

const int MAXN = 1010;
int v[MAXN];    
int w[MAXN];   
int f[MAXN][MAXN]; 

int main() 
{
    int n, m;   
    cin >> n >> m;
    for(int i = 1; i <= n; i++) 
        cin >> v[i] >> w[i];

    for(int i = 1; i <= n; i++) 
        for(int j = 1; j <= m; j++)
        {
            if(j < v[i]) 
                f[i][j] = f[i - 1][j];
            // 能装，需进行决策是否选择第i个物品
            else    
                f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
        }           
    cout << f[n][m] << endl;

}

#include<bits/stdc++.h>

using namespace std;

const int MAXN = 1010;
int f[MAXN];  

int main() 
{
    int n, m;   
    cin >> n >> m;

    for(int i = 1; i <= n; i++) {
        int v, w;
        cin >> v >> w;    
        for(int j = m; j >= v; j--)
            f[j] = max(f[j], f[j - v] + w);
    }

    cout << f[m] << endl;
}

线性dp

dp的下标，涉及[i-1]的话一般从1开始，反之从0开始。

#include<bits/stdc++.h>
using namespace std;

const int N=510,INF=0x3f3f3f3f;
int f[N][N];
int a[N][N];

int main(){
    int n;
    cin>>n;

    for(int i=1;i<=n;i++){
        for(int j=1;j<=i;j++){
            cin>>a[i][j];
        }
    }

    for(int i=1;i<=n;i++){             
        for(int j=0;j<=i+1;j++){          //因为有负数，所以应该将两边设为-INF
        //不然取max出问题了捏
            f[i][j]=-INF;
        }
    }

    f[1][1]=a[1][1];
    for(int i=2;i<=n;i++){
        for(int j=1;j<=i;j++){
            f[i][j]=a[i][j]+max(f[i-1][j-1],f[i-1][j]);
        }
    }

    int res=-INF;
    for(int i=1;i<=n;i++) res=max(res,f[n][i]);
    cout<<res<<endl;
}

这有种倒叙做法很酷。
不用考虑边界问题，因为从下往上转移，下面的东西都有了已经，不会出错，不用赋为-INF，但写个INF也不吃力。
但这种思想还是要掌握。

#include<bits/stdc++.h>
using namespace std;

const int N=510;
int f[N][N];
int n;

int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=i;j++){
            cin>>f[i][j];
        }
    }

    for(int i=n;i>=1;i--){
        for(int j=i;j>=1;j--){
            f[i][j]=max(f[i+1][j],f[i+1][j+1])+f[i][j];
        }
    }
    cout<<f[1][1]<<endl;
}