数据结构与算法：二叉树

二叉树

（一）二叉树

1.二叉树

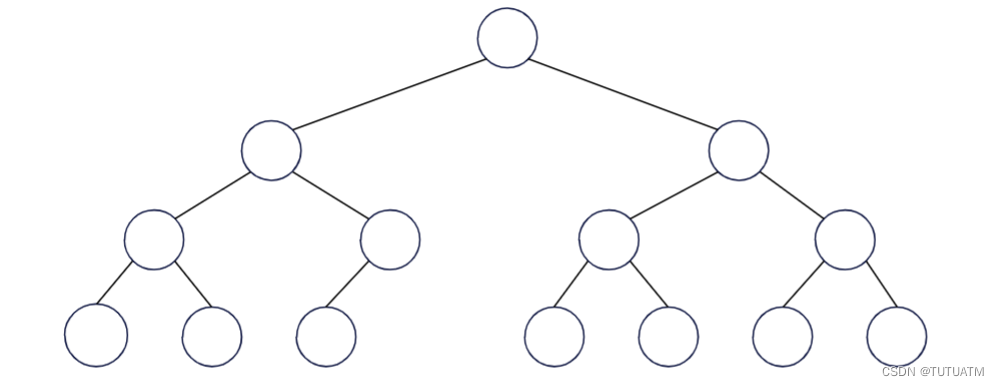
（1）每个节点最多只有两个子节点

---

2.满二叉树

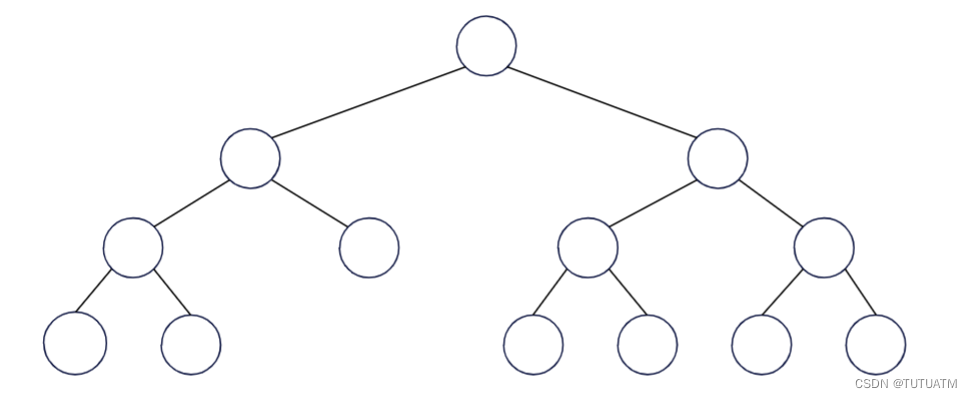
（1）每个节点只有0个或者2个子节点

---

3.完全二叉树

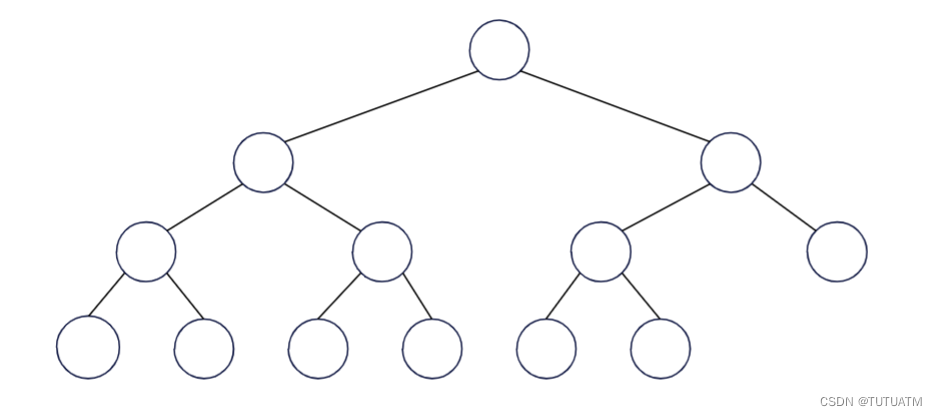
（1）每一层节点缺失的子节点只能在右边

---

4.完美二叉树

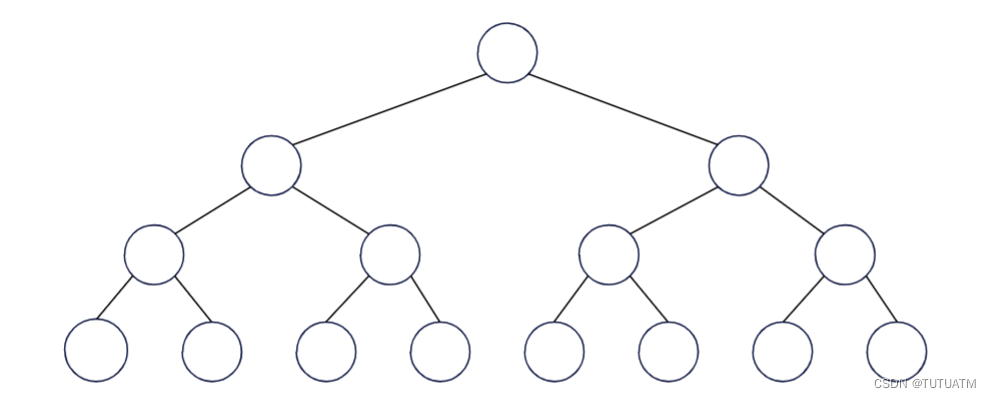
（1）每一层都是满节点

---

（二）二叉树遍历

1.递归

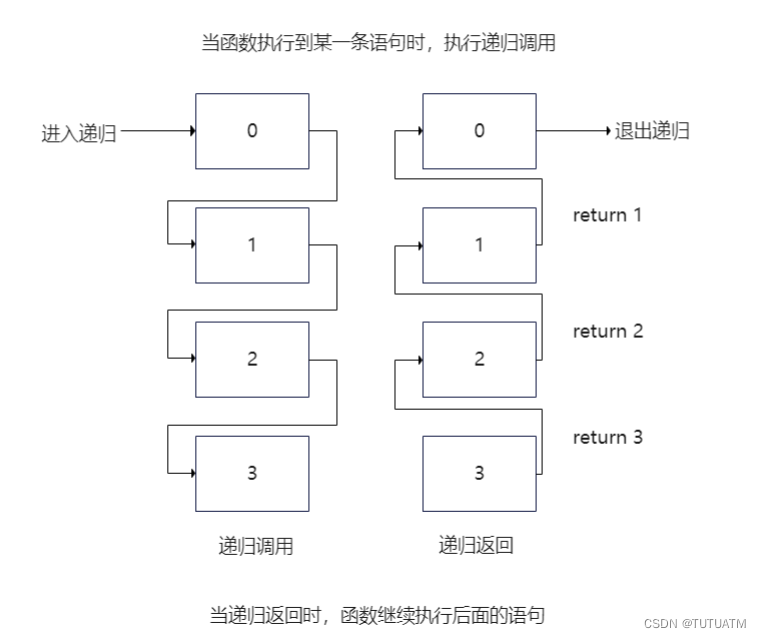
（1）递归退出条件

（2）何时递归

---

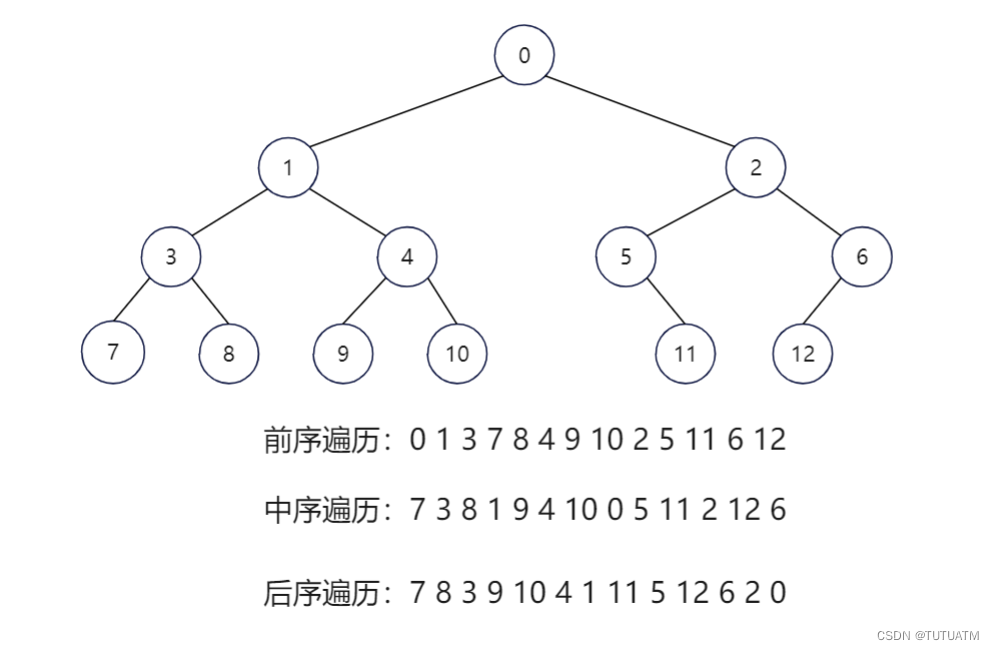
2.前序遍历：访问根节点，遍历左子树，遍历右子树

（1）递归法

void preOrderRecTrav(BinNode* root)
{
	if(root == NULL)
		return;
	printf("%d ",root->data);
	preOrderRecTrav(root->left);
	preOrderRecTrav(root->right);
}

---

（2）迭代法

void preOrderIterTrav(BinNode* root)
{
	stack<BinNode*> s;
	vector<Elem> v;
	
	while(root || !s.empty())
	{
		while(root)
		{
			v.push_back(root->data);
			s.push(root);
			root = root->left;
		}
		
		if(!s.empty())
		{
			root = s.top();
			s.pop();
			root = root->right;
		}
	}
	
	for(int i = 0;i < v.size();i++)
		cout << v.at(i) << " ";
}

---

3.中序遍历：遍历左子树，访问根节点，遍历右子树

（1）递归法

void midOrderRecTrav(BinNode* root)
{
	if(root == NULL)
		return;
	midOrderRecTrav(root->left);
	printf("%d ",root->data);
	midOrderRecTrav(root->right);
}

---

（2）迭代法

void midOrderIterTrav(BinNode* root)
{
	stack<BinNode*> s;
	vector<Elem> v;
	
	while(root || !s.empty())
	{
		while(root)
		{
			s.push(root);
			root = root->left;
		}
		
		if(!s.empty())
		{
			root = s.top();
			v.push_back(root->data);
			s.pop();
			root = root->right;
		}
	}
	
	for(int i = 0;i < v.size();i++)
		cout << v.at(i) << " ";
	
}

---

4.后续遍历：遍历左子树，遍历右子树，访问根节点

（1）递归法

void posOrderRecTrav(BinNode* root)
{
	if(root == NULL)
		return;
	posOrderRecTrav(root->left);
	posOrderRecTrav(root->right);
	printf("%d ",root->data);
}

---

（2）迭代法

void posOrderIterTrav(BinNode* root)
{
	stack<BinNode*> s;
	vector<Elem> v;
	
	while(root || !s.empty())
	{
		while(root)
		{
			v.push_back(root->data);
			s.push(root);
			root = root->right;
		}
		
		if(!s.empty())
		{
			root = s.top();
			s.pop();
			root = root->left;
		}
	}

	reverse(v.begin(),v.end());
	
	for(int i = 0;i < v.size();i++)
		cout << v.at(i) << " ";
	
}

---

5.层序遍历

void layOrderTrav(BinNode* root)
{
	queue<BinNode*> q;
	vector<Elem> v;
	
	q.push(root);

	while(root || !q.empty())
	{
		v.push_back(root->data);
		q.pop();
		if(root->left)
			q.push(root->left);
		if(root->right)
			q.push(root->right);
		
		root = q.front();
	}
	
	for(int i = 0;i < v.size();i++)
		cout << v.at(i) << " ";
}

---

（三）二叉树操作

1.插入

2.遍历

#include <iostream>
using namespace std;

#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <queue>
#include <vector>
#include <algorithm>

#define Elem int

typedef struct BinNode {
	
	Elem data;
	struct BinNode* left;
	struct BinNode* right;
}BinNode;

BinNode* createNode(Elem data)
{
	BinNode* node = (BinNode*)malloc(sizeof(BinNode));
	
	node->data = data;
	node->left = NULL;
	node->right = NULL;
	
	return node;
}

BinNode* findNode(BinNode* root,Elem x)
{
	//中间变量，用于存放下层递归返回值
	BinNode* temp;
	
	if(root == NULL)
		return NULL;
	
	if(root->data == x)
		return root;
	
	temp = findNode(root->left,x);
	return temp?temp:findNode(root->right,x);
}

int insert(BinNode* root,Elem x,int LR,Elem data)
{
	int flag = 0;
	if(root == NULL)
		flag = -1;
	else
	{
		root = findNode(root,x);
		
		if(LR == 0)
		{
			if(root->left == NULL)
				root->left = createNode(data);
			else
				flag = -1;
		}
		else
		{
			if(root->right == NULL)
				root->right = createNode(data);
			else
				flag = -1;
		}
	}
		
	return flag;
}

void preOrderRecTrav(BinNode* root)
{
	if(root == NULL)
		return;
	printf("%d ",root->data);
	preOrderRecTrav(root->left);
	preOrderRecTrav(root->right);
}

void midOrderRecTrav(BinNode* root)
{
	if(root == NULL)
		return;
	midOrderRecTrav(root->left);
	printf("%d ",root->data);
	midOrderRecTrav(root->right);
}

void posOrderRecTrav(BinNode* root)
{
	if(root == NULL)
		return;
	posOrderRecTrav(root->left);
	posOrderRecTrav(root->right);
	printf("%d ",root->data);
}

void preOrderIterTrav(BinNode* root)
{
	stack<BinNode*> s;
	vector<Elem> v;
	
	while(root || !s.empty())
	{
		while(root)
		{
			v.push_back(root->data);
			s.push(root);
			root = root->left;
		}
		
		if(!s.empty())
		{
			root = s.top();
			s.pop();
			root = root->right;
		}
	}
	
	for(int i = 0;i < v.size();i++)
		cout << v.at(i) << " ";
}

void midOrderIterTrav(BinNode* root)
{
	stack<BinNode*> s;
	vector<Elem> v;
	
	while(root || !s.empty())
	{
		while(root)
		{
			s.push(root);
			root = root->left;
		}
		
		if(!s.empty())
		{
			root = s.top();
			v.push_back(root->data);
			s.pop();
			root = root->right;
		}
	}
	
	for(int i = 0;i < v.size();i++)
		cout << v.at(i) << " ";
	
}

void posOrderIterTrav(BinNode* root)
{
	stack<BinNode*> s;
	vector<Elem> v;
	
	while(root || !s.empty())
	{
		while(root)
		{
			v.push_back(root->data);
			s.push(root);
			root = root->right;
		}
		
		if(!s.empty())
		{
			root = s.top();
			s.pop();
			root = root->left;
		}
	}

	reverse(v.begin(),v.end());
	
	for(int i = 0;i < v.size();i++)
		cout << v.at(i) << " ";
	
}

void layOrderTrav(BinNode* root)
{
	queue<BinNode*> q;
	vector<Elem> v;
	
	q.push(root);

	while(root || !q.empty())
	{
		v.push_back(root->data);
		q.pop();
		if(root->left)
			q.push(root->left);
		if(root->right)
			q.push(root->right);
		
		root = q.front();
	}
	
	for(int i = 0;i < v.size();i++)
		cout << v.at(i) << " ";
}


int main()
{
   	/*  Write C code in this online editor and run it. */
	BinNode* root = createNode(0);
	
	insert(root,0,0,1);
	insert(root,0,1,2);
	insert(root,1,0,3);
	insert(root,1,1,4);
	insert(root,2,0,5);
	insert(root,2,1,6);
	insert(root,3,0,7);
	insert(root,3,1,8);
	insert(root,4,0,9);
	insert(root,4,1,10);
	insert(root,5,1,11);
	insert(root,6,0,12);
	
	cout << "递归遍历:"<<endl;
	preOrderRecTrav(root);
	cout <<endl;
	midOrderRecTrav(root);
	cout <<endl;
	posOrderRecTrav(root);
	cout <<endl<<endl<< "迭代遍历:"<<endl;
	preOrderIterTrav(root);
	cout <<endl;
	midOrderIterTrav(root);
	cout <<endl;
	posOrderIterTrav(root);
	cout <<endl<<endl<< "层序遍历:" <<endl;
	layOrderTrav(root);
   
   	return 0;
}