Python用Scipy作数据插值

最新推荐文章于 2025-04-24 13:13:38 发布

HarvestII

最新推荐文章于 2025-04-24 13:13:38 发布

阅读量6.2k

点赞数 11

分类专栏： python

本文链接：https://blog.youkuaiyun.com/weixin_45008173/article/details/107094422

版权

python 专栏收录该内容

9 篇文章

订阅专栏

本文深入探讨SciPy库中的插值技术，包括线性插值、样条插值、拉格朗日插值及多维插值。通过数学原理解析和代码示例，展示不同插值方法的应用场景和实现细节。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章目录

概述

写在前面 😀😀😀😀😀：
因为SciPy有很多的板门，我这个是基于SciPy1.5.0的文档进行解释的。如果后者看到这篇博客，建议先确定一下自己使用多个版本。
Sciy是什么？

SciPy is a collection of mathematical algorithms and convenience functions built on the NumPy extension of Python. It adds significant power to the interactive Python session by providing the user with high-level commands and classes for manipulating and visualizing data. With SciPy, an interactive Python session becomes a data-processing and system-prototyping environment rivaling systems, such as MATLAB, IDL, Octave, R-Lab, and SciLab.

这是官方解释的第一段话，主要就是下面几个点：

基于numpy的Python扩展
提供一些高层的数学方法和数据可视化命令
水平很高，功能比较强大

基础

SciPy有很多模块，我们在对数据进行插值时，使用核心模块的是scipy.interpolate这个模块，其他部分也会有使用，使用到会以注释的形式给出解释。

插值的数学原理

分段线性插值

分段线性插值的基本原理就是把相邻的两个节点连起来，从而实现节点两两之间的线性插值，我们这条分段的折线记作 $I_n(x_i) =y_i$ ，且 $I_n(x_i)$ 在每个小区间 $x_i,x_{i+1}]$ 上都是线性函数。
直接我们可以通过一系列推导(推导方法写在后面)得出 $I_n$ 的表达式 $I_n(x) = \sum_{i=0}^ny_il_i(x)$ ：
$l_i(x)= \begin{cases} \cfrac {x-x_i}{x_i-x_{i-1}} &x\in[x_i,x_{i+1}],i\neq0 \\ \\ \cfrac {x-x_{i+1}}{x_{i}-x_{i+1}} &x\in[x_{i+1},x_{i+2}],i\neq0 \\ \\ 0& \text{其他} \end{cases}$
可以发现当 $x\in[a,b]$ 时， $I_n(x)$ 的收敛性是很好的：
$\lim_{n\rightarrow\infin} I_n(x) = f(x)$
推导方法：（该推导方法只是方便理解，并非真正的推导过程）
我们选择使用三个点 $x_1,x_2$ ，他们对应的函数值分别是 $y_1,y_2$ :
由 $\cfrac {y_2-y_1}{x_2-x_1}(x-x1)+y1$
得 $\cfrac {x-x_1}{x_2-x_1}(y_2-y_1)+y1$
拆开化简得
$\cfrac{x-x_1}{x_2-x_1}y_2+\cfrac{x-x_2}{x_1-x_2}y_1$
理解完毕。
从上面模式我们可以看出，如果要进行这种插值，我们只需要获得 $(x, y)$ 的点坐标就够了。具体代码实现：

### 引入库函数
import numpy as np 
from scipy import interpolate as inter
import matplotlib.pyplot as plt
from scipy import constants as Const

x = np.linspace(0,4,5) #使用numpy中的linspace方法生成[0,4]之间等间距的5个数
y = np.sin(x)
f = inter.interp1d(x,y,kind ="linear") #进行线性插值
xli = np.linspace(0,4,50)
yli = f(xli)
yreal = np.sin(xli)
plt.plot(x,y,'o',xli,yli,'-',xli,yreal,'--') #配置图像
plt.legend(['data','linear','real'], loc='best') #配置图标
plt.show() #展示图像

结果图在这里插入图片描述
解释一下interp1d这个方法：

class scipy.interpolate.interp1d(x, y, kind='linear',\ 
 axis=- 1, copy=True, bounds_error=None,\
  fill_value=nan, assume_sorted=False)

x和y就是点坐标向量，这两个值得类型为ndarray，就是numpy支持得那个类，如果是python得array可以通过

x = np.ararry([1,2,3,4]) #可以转化

第三个kind就是interpr1d的扩展方法，他不光可以做分段线性插值，还可以进行：

‘linear’, ‘nearest’, ‘zero’, ‘slinear’, ‘quadratic’,‘cubic’, ‘previous’, ‘next’, where ‘zero’, ‘slinear’, ‘quadratic’ and ‘cubic’ refer to a spline interpolation of zeroth, first, second or third order

样条插值
最邻近插值
……

效果图如下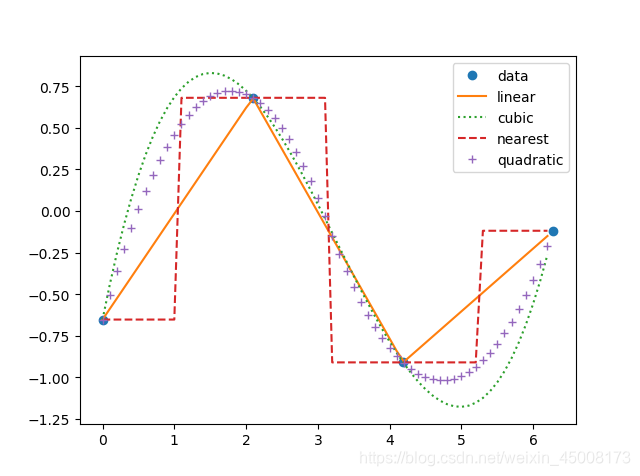：在这里插入图片描述
代码：

x = np.linspace(0,constants.pi*2,4)
y = np.cos(x**2/3+4)
xli = np.arange(0,constants.pi*2,0.1)
fli = inter.interp1d(x,y,kind ="linear")
yli = fli(xli)
ycub = inter.interp1d(x,y,kind ="cubic")(xli)
ynear = inter.interp1d(x,y,kind ="nearest")(xli)
yquadratic = inter.interp1d(x,y,kind ="quadratic")(xli)

plt.plot(x,y,'o',xli,yli,'-')
plt.plot(xli,ycub,':',xli,ynear,'--',xli,yquadratic,'+')
plt.legend(['data','linear','cubic','nearest','quadratic'],loc='best')
plt.show()

上面的方法包含了，线性插值，三次样条插值，最邻近插值，二次样条插值，还有一种插值方法，为拉格朗日插值。

拉格朗日插值

注意，拉格朗日插值的不好的点就在于点的个数越多，多项式的阶就会变高，这样为我们的计算带来很大的障碍。所以我们这里只是见到那介绍，是否使用看你的需求啦。原理：他描述的不错

咱们直接上代码，拉格朗日插值并不是被interp1d方法包含的。他有一个专门的方法，就叫lagrange插值法，方法介绍：

scipy.interpolate.lagrange(x, w)
Return a Lagrange interpolating polynomial.Given two 1-D arrays x and w, returns the Lagrange interpolating polynomial through the points (x, w).
Warning: This implementation is numerically unstable. Do not expect to be able to use more than about 20 points even if they are chosen optimally.

依然注意最后一句，这也是我开篇说那句话的原因，上代码：

from scipy.interpolate import lagrange
x = np.array([0, 1, 2])
y = x**3
poly = lagrange(x, y)
print(list(poly))
#结果
[ 3., -2.,  0.]

可以发现我一共插入了3个点，拉格朗日插值就会产生3个阶数为2的多项式，然后解出三个系数，系数的向量就是返回的结果，他们从低次到高次排列。

样条插值

前面已经介绍了样条插值的一种函数表示，并没有介绍其数学原理，这里来解释一下。并给出SciPy的功能更全面的的样条插值方法。
原来工人们为了画出圆滑的曲线，都会在两个点之间放一个样条，然后沿着样条将去先画出，这也是样条插值叫法的来源。那么从这个故事上应该可以直观的感受到，样条插值应该是在两点之间建立起一个多项式。
但是这个多项式怎样做到在点与点之间平滑呢？那就是他们的导数在该点相等。正式定义：
给定区间 $[a, b]$ ,做出如下划分
$\triangle :a = x_0<x_1<x_2<\cdots<x_{n-1}<x_n =b$
如果函数 $S (x)$ 满足
4. 每个小区间 $x_i,x_{i+1}]$ 上方程 $S (x)$ 为 $m$ 次多项式。
5. $S (x)$ 在 $[a, b]$ 上具有 $m - 1$ 阶连续导数。
那么称 $S (x)$ 为样条函数，显然分段线性插值方法为一次样条函数。

三次样条函数大多数教材教材讲的挺多，这里截图的是司守奎老师在数学建模文章中提到的：
在这里插入图片描述
解释一下上面的一些参数怎么得来的：
为什么会有4n-2个方程，我们可以理解成一共有n+1个点，但是由于边界点即 $x_0$ 和 $x_n$ 不能保证边界可导，这两个点不能得出（5.2）中的三个等式，所以这样就会有 $4 (n + 1) - 3 * 2 = 4 n - 2$ 。那少两个式子怎么处理呢？下面给出了的三种方法，但是其实我们实际插值的时候不用考虑这个问题，我也不知道SciPy里面到底怎么插值的，他没有给出具体的解释。
对于样条插值，又是我们并不一定只需要样条插值产生的曲线，有可能还需要样条的导数，样条的积分，那么之前的方法就不足以我们去作这件事情了，SciPy提供了另外一个更适合样条插值的类Spline，官方解释：
在这里插入图片描述
提取一下重点：

进行插值之前有两个重要步骤：（1）计算出一个样条曲线的代表（2）样条预期点被估计
获取样条曲线代表的方法有两种，直接获取，参数填入获取。
在2维平面上使用splrep这个方法。这个方法将会在下面解释。
N维空间使用splprep这方法允许参数化的定义曲面，然后就解释了一下这个方法。
有一个关键参数s，这个参数应该识smoothing的简写，是用来调整图像平滑度的s有个方程，s的默认值有个关于m的计算方法(见上图)，m为估计点的数量。如果没有出图光滑度的要求，把S赋值为0就是常规的默认数值。
Spline不光可以进行N维插值，由于他的可导性，我们还能搞定它导数、积分的曲线，超过8个点的三次样条插值还能估计样条曲线的根的取值。

x = np.linspace(0,10,12)
y = np.exp(x**2+3*x)
tck = inter.splrep(x,y,s = 0) 
xnew = np.linspace(0,10,120)
ynew = inter.splev(xnew,tck,der =0)
plt.figure()
plt.plot(x, y, 'x', xnew, ynew, '--',xnew, np.exp(xnew**2+3*xnew))
plt.legend(['data','Cubic Spline','True'])
plt.title('Cubic-spline interpolation')
plt.show()

图像：
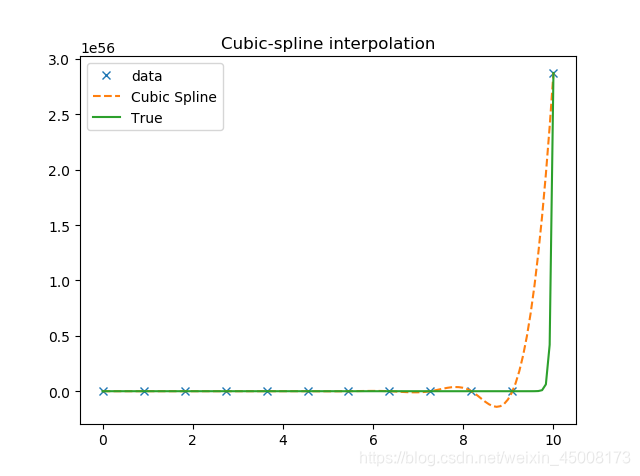
在这里插入图片描述
解释splrep这个方法，方法解释传送门
注意splev这个方法它可以求导，其中控制参数为der，der来求几阶导数。方法解释传送门
代码：

x = np.linspace(0,10,12)
y = np.sin(x)
tck = inter.splrep(x,y,s = 0)
xnew = np.linspace(0,10,120)
ynew = inter.splev(xnew,tck,der =1)
plt.figure()
plt.plot(xnew, ynew, '--',xnew, np.cos(xnew))
plt.legend(['Der of Cubic Spline','True'],loc='upper right')
plt.title('Der of Cubic-spline interpolation')
plt.show()

图形：
在这里插入图片描述
积分方法：

def integ(x, tck, constant=-1):
    x = np.atleast_1d(x)
    out = np.zeros(x.shape, dtype=x.dtype)
    for n in range(len(out)):
        out[n] = inter.splint(0, x[n], tck)
    out += constant
    return out
x = np.linspace(0,10,12)
y = np.sin(x)
xnew = np.linspace(0,10,120)   
tck = inter.splrep(x,y,s = 0) 
yint = integ(xnew, tck)
plt.figure()
plt.plot(xnew, yint, xnew, -np.cos(xnew), '--')
plt.legend(['Integ of Cubic Spline', 'True'],loc = 'upper right')
plt.title('Integral estimation from spline')
plt.show()

在这里插入图片描述

多维插值

多维插值使用的是griddata这个方法来来进行二维空间插值，这里给出一个该方法的解释：官方传送门

scipy.interpolate.griddata(points, values, xi, method='linear', fill_value=nan, rescale=False)

该方法支持多种插值方式，直接上代码例子来看一下吧，本次代码上由于要保证图形显示所以会用到一些复杂的方法，这里会给出注释，详细内容请查看官方文档跳转：

def func(x,y):
    return x*(1-x)*np.cos(4*np.pi*x**2) * np.sin(4*np.pi*y**2)
grid_x , grid_y = np.mgrid[0:1:100j,0:1:100j] #形成1X1的等间隔格网
points = np.random.rand(1000,2) #生成1000x2的随机数，值介于[0,1]之间
value = func(points[:,0],points[:,1]) #代入第一列和第二列
grid_zli = inter.griddata(points,value,(grid_x, grid_y), method = 'linear')#将点和值查到网格中，方法为线性
grid_zCu = inter.griddata(points,value,(grid_x, grid_y), method ='cubic')
grid_znea = inter.griddata(points,value,(grid_x, grid_y), method ='nearest')
plt.figure()#开始产生图形
plt.subplot(221)#设置副图的位置
fig1 = plt.imshow(func(grid_x, grid_y), extent=(0,1,0,1), origin='lower',cmap='spring')#展示图片，cmap配色为spring，origin为配置原点，默认为upper不符合我们的习惯
plt.plot(points[:,0], points[:,1], 'k.', ms=1) #讲点显示到图上
plt.colorbar(fig1)#对fig1配置colorbar
plt.title('Original')#图像题目设置成Original
plt.subplot(222)
fig2 = plt.imshow(grid_zli.T, extent=(0,1,0,1), origin='lower',cmap='summer')
plt.colorbar(fig2)
plt.title('Linear')
plt.subplot(223)
fig3 = plt.imshow(grid_zCu.T, extent=(0,1,0,1), origin='lower',cmap='autumn')
plt.colorbar(fig3)
plt.title('Cubic')
plt.subplot(224)
fig4 = plt.imshow(grid_znea.T,extent=(0,1,0,1), origin='lower',cmap='winter')
plt.colorbar(fig4)
plt.title('Nearest')
plt.gcf().set_size_inches(6, 6)
plt.show()