图优化库g2o中的节点(Vertex)和边(Edge)

陌~路~人

已于 2023-01-17 15:14:30 修改

阅读量2.1k

点赞数 1

分类专栏： g2o 文章标签：算法

于 2023-01-17 09:58:39 首次发布

本文链接：https://blog.youkuaiyun.com/weixin_44884561/article/details/128706473

版权

g2o 专栏收录该内容

2 篇文章

订阅专栏

文章介绍了图优化的基本概念，以非线性最小二乘问题为例，展示了如何用图结构表示优化问题。g2o是一个图优化库，采用通用超图结构处理优化问题，分为图优化架构、优化算法和线性求解器三层。OptimizableGraph类用于表示节点和边，提供基类如BaseVertex和BaseUnaryEdge用于自定义节点和边。优化过程中，使用BlockSolver和不同的线性求解器如CSparse、Cholmod等解决线性系统。最后，通过一个视觉SLAM的代码示例展示了g2o在实际问题中的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、图优化简介

图优化本质上仍然是非线性优化。只不过利用图的方式表现出来，使问题可视化，然后可以根据可视化的结果来更好的调整优化过程。

图是一种数据结构。在图优化中，用节点 (vertex) 表示优化变量，用边 (edge) 表示误差项。于是，对于任意一个上述形式的非线性最小二乘问题，都可以构建一个与之对应的图。

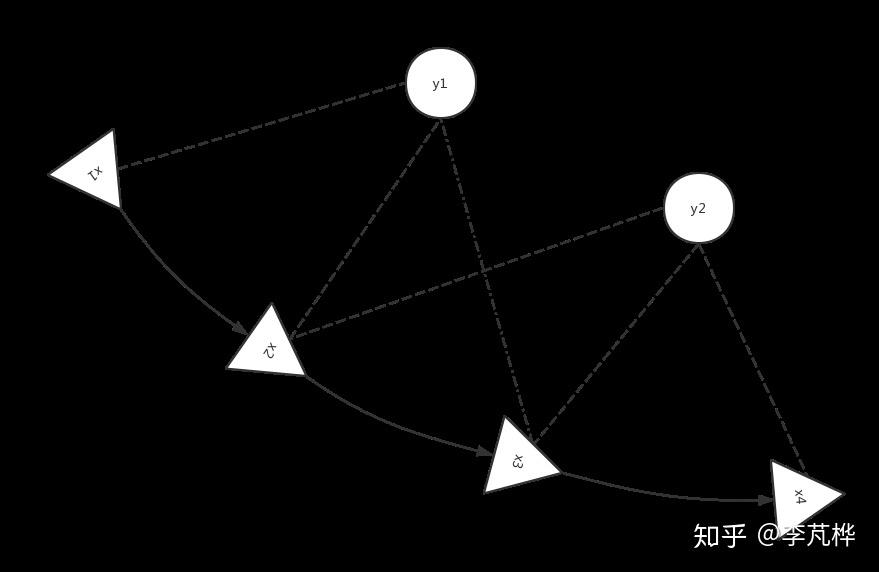
以视觉SLAM为例，用三角形表示相机，圆表示路标，它们共同构成了图优化的顶点；用实线表示相机的运动模型，用虚线表示观测模型，它们构成了图优化的边。则图就表示如下图所示：

二、g2o简介

g2o 是一个是一个图优化库，它使用一个generic hyper-graph 结构来表达一个优化问题。其内部类关系图如下图所示：

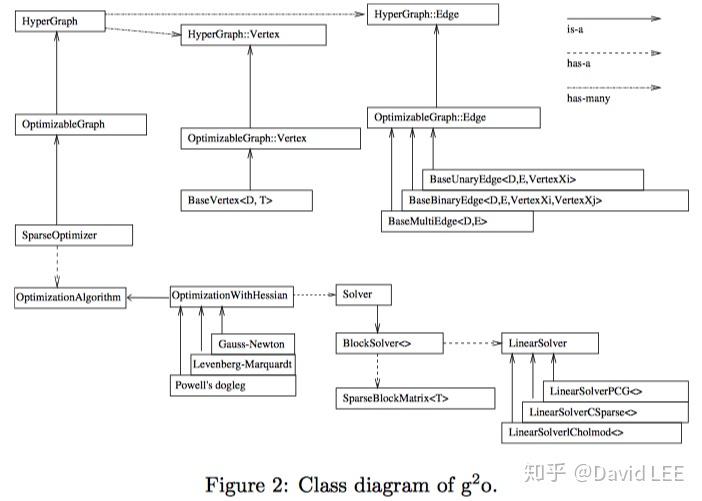
由这张图可以看出，整个g2o的架构分为了三层：

外层的图优化架构：包含了图、节点和边等等。这也是最主要的和用户进行交互的一层，用于构建整个优化问题

中间的优化算法：这是具体的最小二乘优化算法，包括了GN、LM和狗腿算法。用户一般只要选择某个优化算法即可（根据问题性质），并不用太关心内部实现。而且，在g2o中，这些优化算法只专注于本次迭代中的求解，至于说何时停止、如何更新节点都是外层的图优化来维护的

最里层的线性求解器：这是所有优化算法的核心，即如何高效求解一个大型（稀疏或稠密）的线性系统 (Hx=b)，也是最复杂的。除非对效率由极致追求（必须选择最合适的计算方式），否则用户一般不关心

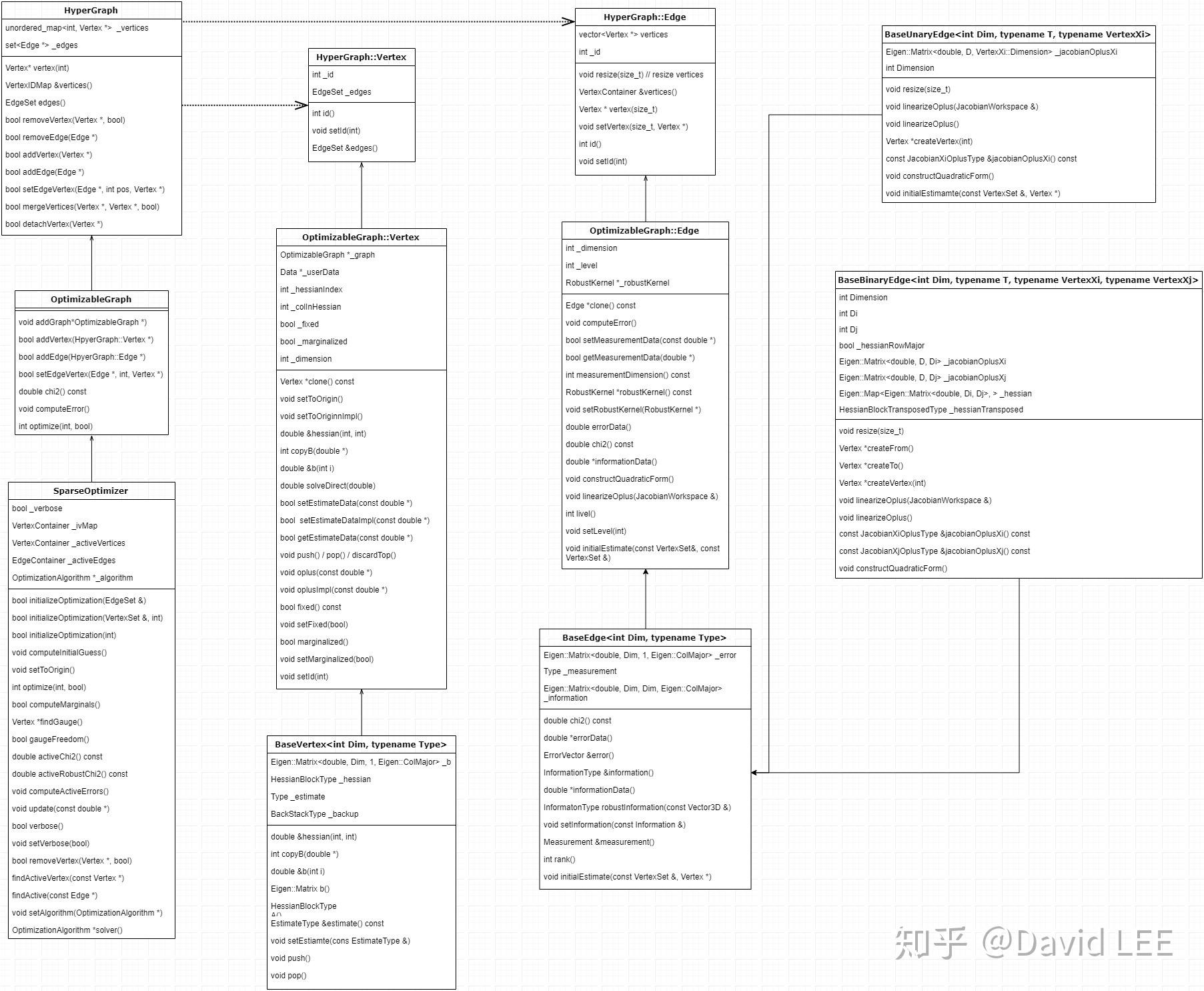
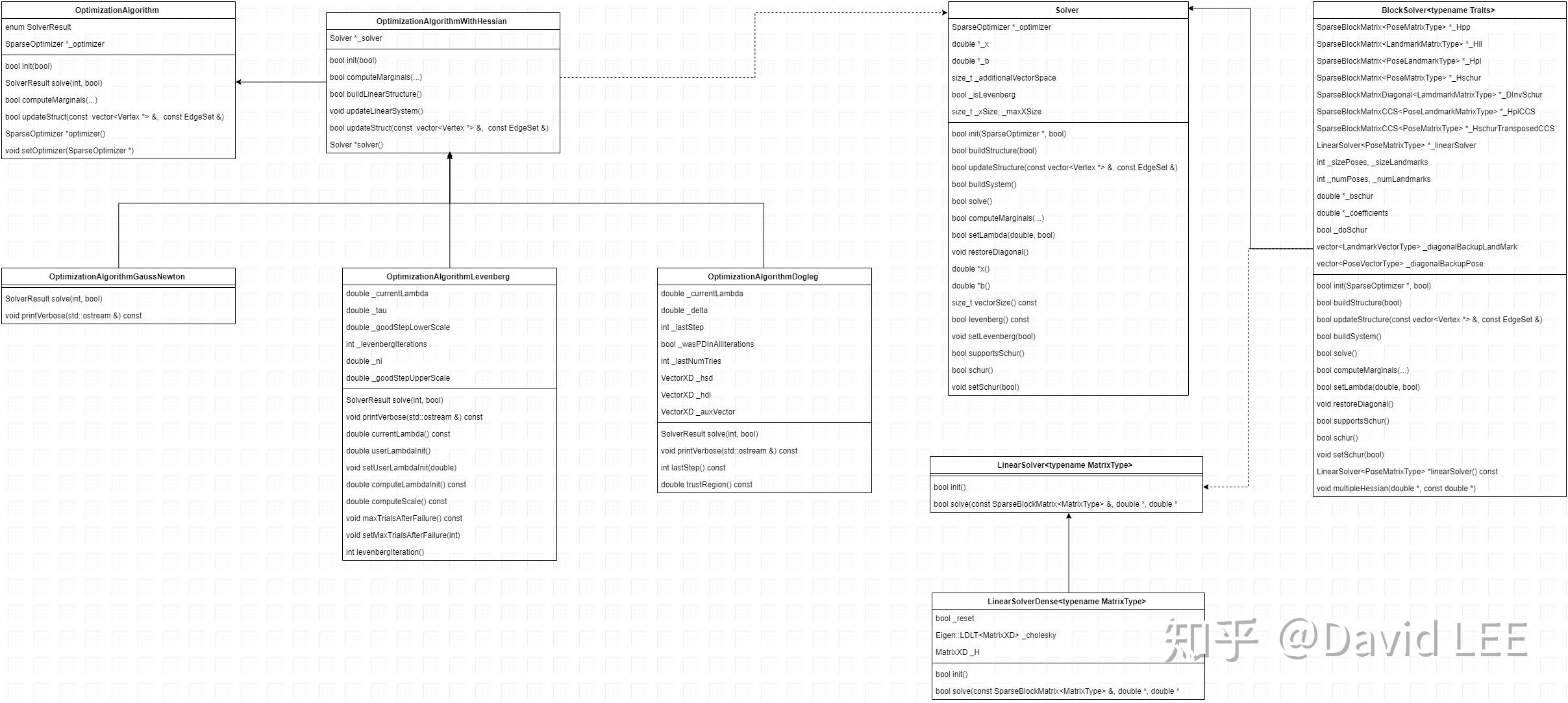
g2o中个各类的属性和方法如下图所示:

三、OptimizableGraph

类OptimizableGraph 定义在optimizable_graph.h 中。两个内部类OptimizableGraph::Vertex 和OptimizableGraph::Edge 来表示节点和超边。这两个类比较基础，所以系统也提供了一些模版类来协助扩展

1、BaseVertex

_estimate：储存节点的值

setToOriginImpl()：重置节点的值

setEstimate(type)：定义估计值

setId(int) ：定义节点编号

oplusImpl(type)：节点的更新函数

  class myVertex: public g2::BaseVertex<Dim, Type>
  {
      public:
      EIGEN_MAKE_ALIGNED_OPERATOR_NEW
      
      myVertex(){}
      
      virtual void read(std::istream& is) {}
      virtual void write(std::ostream& os) const {}
      
      virtual void setOriginImpl()
      {
          _estimate = Type();
      }
      virtual void oplusImpl(const double* update) override
      {
          _estimate += /*update*/;
      }
  }

2、BaseUnaryEdge

_measurement：存储观测值

_error：存储误差

_vertices[]：存储节点

setId(int)：定义边的编号

setMeasurement(type)：定义观测值

setVertex(int, vertex)：设置连接的节点

setInformation()：设置信息矩阵（协方差矩阵之逆）

linearizeOplus()：计算雅可比矩阵

computeError()：计算误差

_jacobianOplusXi：雅可比矩阵，由Eigen::Matrix<观测维度，节点维度>定义而来

lass myEdge: public g2o::BaseBinaryEdge<errorDim, errorType, Vertex1Type, Vertex2Type>
  {
      public:
      EIGEN_MAKE_ALIGNED_OPERATOR_NEW
      
      myEdge(){}
      
      virtual bool read(istream& in) {}
      virtual bool write(ostream& out) const {}
      
      virtual void computeError() override
      {
          // ...
          _error = _measurement - Something;
      }
      
      virtual void linearizeOplus() override
      {
          _jacobianOplusXi(pos, pos) = something;
          // ...
          
          /*
          _jocobianOplusXj(pos, pos) = something;
          ...
          */
      }
      
      private:
      // data
  }

四、Solver

最小二乘中的一个问题就是求解线性系统 $\text{[math]}$ ，为此，g2o 提供了Solver 类。但利用Solver 类进行优化需要设置很多参数。所以g2o 提供了模版类BlockSolver<> （内置了SparseBlockMatrix<> 类）来简化流程。BlockSolver<> 可以进行Schur 消元并利用另一个模版类LinearSolver<> 来求解。g2o 提供了多种线性求解器，包括CSparse, CHOLMOD 等等。

  #include <g2o/core/base_vertex.h>
  #include <g2o/core/base_binary_edge.h> // base_unary_edge.h
  #include <g2o/core/block_solver.h>
  #include <g2o/core/optimization_algorithm_levenberg.h>
  #include <g2o/core/optimization_algorithm_gauss_newton.h>
  #include <g2o/core/optimization_algorithm_dogleg.h>
  #include <g2o/solvers/dense/linear_solver_dense.h>
  
  int main(int argc char** argv)
  {
      typedef g2o::BlockSolver<g2o::BlockSolverTraits<poseDim, landmarkDim> > Block;
      
      // 线性方程求解器
      // linear solver using dense cholesky decompositio
      Block::LinearSolverType* linearSolver = new g2o::LinearSolverDense<Block::PoseMatrixType>(); //稠密增量方程
      
      // linear solver which uses the sparse Cholesky solver from Eigen
      // Block::LinearSolverType* linearSolver = new g2o::LinearSolverEigen<Block::PoseMatrixType>();
      
      // linear solver which uses CSparse
      // Block::LinearSolverType* linearSolver = new g2o::LinearSolverCSparse<Block::PoseMatrixType>();
      
      // basic solver for Ax = b which has to reimplemented for different linear algebra libraries
      // Block::LinearSolverType* linearSolver = new g2o::LinearSolverCholmod<Block::PoseMatrixType>();
      
      Block* solver_ptr = new Block(linearSolver); // 矩阵块求解器，设置线形求解器
      
      // 梯度下降法
      g2o::optimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLenvnberg(solver_ptr);
      
      // g2o::optimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton(solver_ptr);
      
      //g2o::optimizationAlgorithmGaussDogleg* solver = new g2o::OptimizationAlgorithmDogleg(solver_ptr);
      
      g2o::SparseOptimizer optimizer; // 图模型
      
      optimizer.setAlgorithm(solver); // 设置求解器
      // optimizer.setVerbose(true); // 打开调试输出
      
      // vertex
      g2o::VertexSE3Expmap* pose = new g2o::VeretxSE3Expmap(); // 相机位姿
      pose->setId(0);
      pose->setEstimate(/*something*/);
      optimizer.addVertex(pose);
      
      int index = 1;
      for (const Point p : points) // 伪码
      {
          g2o::PointType* point = new g2o::pointType(); // 伪码
          point->setId(index++);
          point->setEstimate(/*something*/);
          // point->setMarginalized(true); // 该点在解方程时进行Schur消元
          
          optimizer->addVertex(point);
      }
      
      // parameter: camera intrinsics 可有可无
      g2o::CameraParameters* camera = new g2o::CameraParameters(/*K*/);
      camera->setId(0);
      optimizer.addParameter(camera);
      
      // edges
      index = 1;
      for (const Point2d p : point_2d) // 伪码
      {
          g2o::EdgeType* edge = new g2o::EdgeType(); // 伪码
          edge->setId(index);
          // huber loss, 默认为不用设置
          /*
          if (robustify)
          {
              g2o::RobustKernelHuber* rk = new g2o::RobustKernelHuber;
              rk->setDelta(1.0);
              edge->setRobustKernel(rk);
          }
          */
          edge->setVertex(0, dynamic_cast<g2o::PointType*>(optimizer.vertex(index))); // 二元边，第一个顶点为节点
          edge->setVertex(1, pose); // 第二个顶点为相机
          
          edge->setMeasurement(/*something*/);
          // edge->setParameterId(0, 0);
          edge->setInformation(/*Identity*/); // 协方差矩阵之逆
          
          optimizer.addEdge(edge);
          index++;
      }
      
      
      optimizer.setVerbose(true);
      optimizer.initializeOptimization();
      optimizer.optimize(/*iteration times*/);
      return 0;
  }

五、代码示例

视觉SLAM十四讲部分代码

#include <iostream>
#include <opencv2/core/core.hpp>
#include <opencv2/features2d/features2d.hpp>
#include <opencv2/imgcodecs/legacy/constants_c.h>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/calib3d/calib3d.hpp>
#include <Eigen/Core>
#include <g2o/core/base_vertex.h>
#include <g2o/core/base_unary_edge.h>
#include <g2o/core/sparse_optimizer.h>
#include <g2o/core/block_solver.h>
#include <g2o/core/solver.h>
#include <g2o/core/optimization_algorithm_gauss_newton.h>
#include <g2o/solvers/dense/linear_solver_dense.h>
#include <sophus/se3.hpp>
#include <chrono>

class VertexPose : public g2o::BaseVertex<6, Sophus::SE3d> {
public:
  EIGEN_MAKE_ALIGNED_OPERATOR_NEW;

  virtual void setToOriginImpl() override {
    _estimate = Sophus::SE3d();
  }

  /// left multiplication on SE3
  virtual void oplusImpl(const double *update) override {
    Eigen::Matrix<double, 6, 1> update_eigen;
    update_eigen << update[0], update[1], update[2], update[3], update[4], update[5];
    _estimate = Sophus::SE3d::exp(update_eigen) * _estimate;
  }

  virtual bool read(istream &in) override {}

  virtual bool write(ostream &out) const override {}
};

class EdgeProjection : public g2o::BaseUnaryEdge<2, Eigen::Vector2d, VertexPose> {
public:
  EIGEN_MAKE_ALIGNED_OPERATOR_NEW;

  EdgeProjection(const Eigen::Vector3d &pos, const Eigen::Matrix3d &K) : _pos3d(pos), _K(K) {}

  virtual void computeError() override {
    const VertexPose *v = static_cast<VertexPose *> (_vertices[0]);
    Sophus::SE3d T = v->estimate();
    Eigen::Vector3d pos_pixel = _K * (T * _pos3d);
    pos_pixel /= pos_pixel[2];
    _error = _measurement - pos_pixel.head<2>();
  }

  virtual void linearizeOplus() override {
    const VertexPose *v = static_cast<VertexPose *> (_vertices[0]);
    Sophus::SE3d T = v->estimate();
    Eigen::Vector3d pos_cam = T * _pos3d;
    double fx = _K(0, 0);
    double fy = _K(1, 1);
    double cx = _K(0, 2);
    double cy = _K(1, 2);
    double X = pos_cam[0];
    double Y = pos_cam[1];
    double Z = pos_cam[2];
    double Z2 = Z * Z;
    _jacobianOplusXi
      << -fx / Z, 0, fx * X / Z2, fx * X * Y / Z2, -fx - fx * X * X / Z2, fx * Y / Z,
      0, -fy / Z, fy * Y / (Z * Z), fy + fy * Y * Y / Z2, -fy * X * Y / Z2, -fy * X / Z;
  }

  virtual bool read(istream &in) override {}

  virtual bool write(ostream &out) const override {}

private:
  Eigen::Vector3d _pos3d;
  Eigen::Matrix3d _K;
};

void bundleAdjustmentG2O(
  const VecVector3d &points_3d,
  const VecVector2d &points_2d,
  const Mat &K,
  Sophus::SE3d &pose) {

  // 构建图优化，先设定g2o
  typedef g2o::BlockSolver<g2o::BlockSolverTraits<6, 3>> BlockSolverType;  // pose is 6, landmark is 3
  typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType> LinearSolverType; // 线性求解器类型
  // 梯度下降方法，可以从GN, LM, DogLeg 中选
  auto solver = new g2o::OptimizationAlgorithmGaussNewton(
    g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));
  g2o::SparseOptimizer optimizer;     // 图模型
  optimizer.setAlgorithm(solver);   // 设置求解器
  optimizer.setVerbose(true);       // 打开调试输出

  // vertex
  VertexPose *vertex_pose = new VertexPose(); // camera vertex_pose
  vertex_pose->setId(0);
  vertex_pose->setEstimate(Sophus::SE3d());
  optimizer.addVertex(vertex_pose);

  // K
  Eigen::Matrix3d K_eigen;
  K_eigen <<
          K.at<double>(0, 0), K.at<double>(0, 1), K.at<double>(0, 2),
    K.at<double>(1, 0), K.at<double>(1, 1), K.at<double>(1, 2),
    K.at<double>(2, 0), K.at<double>(2, 1), K.at<double>(2, 2);

  // edges
  int index = 1;
  for (size_t i = 0; i < points_2d.size(); ++i) {
    auto p2d = points_2d[i];
    auto p3d = points_3d[i];
    EdgeProjection *edge = new EdgeProjection(p3d, K_eigen);
    edge->setId(index);
    edge->setVertex(0, vertex_pose);
    edge->setMeasurement(p2d);
    edge->setInformation(Eigen::Matrix2d::Identity());
    optimizer.addEdge(edge);
    index++;
  }

  chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
  optimizer.setVerbose(true);
  optimizer.initializeOptimization();
  optimizer.optimize(10);
  chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
  chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
  cout << "optimization costs time: " << time_used.count() << " seconds." << endl;
  cout << "pose estimated by g2o =\n" << vertex_pose->estimate().matrix() << endl;
  pose = vertex_pose->estimate();
}