第二章 统计学基础（三）假设检验

一、假设检验的基本问题

1.1假设问题的提出

什么是假设(hypothesis)：对总体参数的的数值所作的一种陈述

什么是假设检验：事先对总体参数或分布形式作出某种假设，然后利用样本信息来判断原假设是否成立。采用逻辑上的反证法，依据统计上的小概率原理。

1.2提出原假设和备择假设：

①原假设：待检验的假设，又称“0假设”。研究者想收集证据予以反对的假设。总是有=, < 或>。

表示为H0

②备择假设：与原假设对立的假设。表示为 H1。

1.3 假设检验中的两类错误

①第一类错误（弃真错误）：原假设为真时拒绝原假设

第一类错误的概率为α，被称为显著性水平

②第二类错误（取伪错误）：原假设为假时接受原假设

第二类错误的概率为β(Beta)

1.4 假设检验的流程

①提出假设 ②确定适当的检验统计量 ③规定显著性水平α ④计算检验统计量的值 ⑤统计决策

什么是检验统计量？选择统计量的方法与参数估计相同，需考虑：是大样本还是小样本 、总体方差已知还是未知

什么是显著性水平？原假设为真时，拒绝原假设的概率，被称为抽样分布的拒绝域。常用的α值有0.01, 0.05, 0.10。由研究者事先确定。

如何作出统计决策？根据给定的显著性水平α，查表得出相应的临界值。将检验统计量的值与 水平的临界值进行比较。

1.5 利用P值进行决策

如果原假设为真，P-值是抽样分布中大于或小于样本统计量的概率。

左侧检验时，P-值小于等于检验统计量部分的面积。

右侧检验时，P-值大于等于检验统计量 部分的面积

被称为观察到的(或实测的)显著性水平

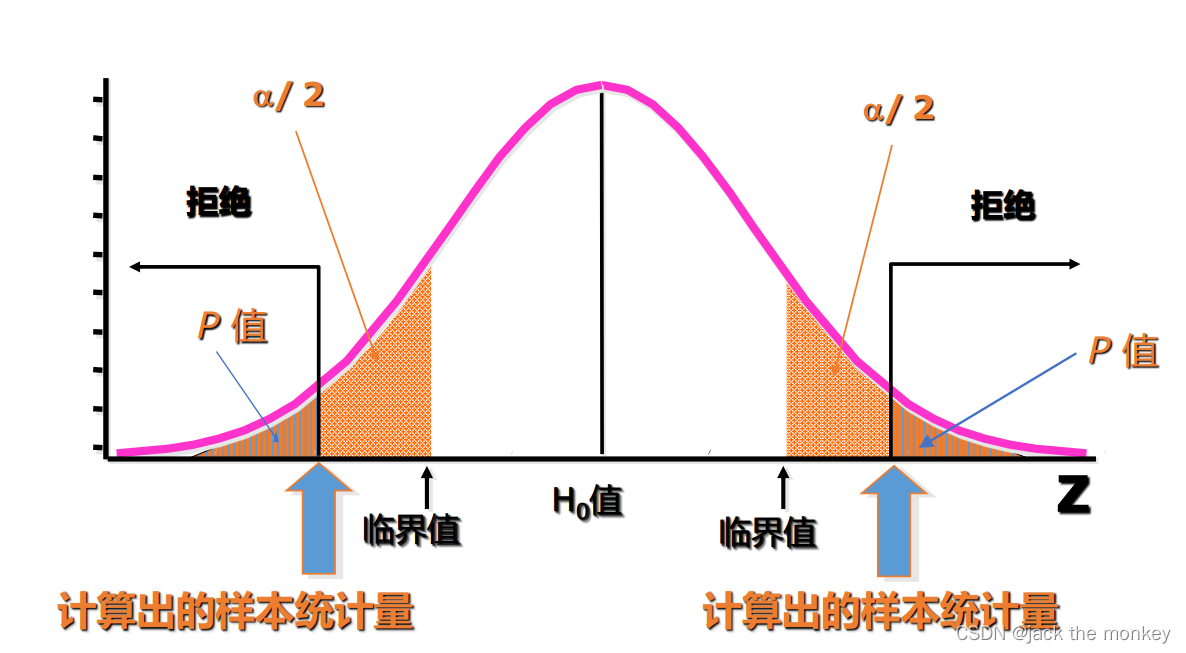
 决策准则