第二章 统计学基础（二）

第五章 参数估计

5.1基本概念

估计量：用于估计总体参数的随机变量。

参数用θ 表示，估计量用θ帽表示。如果样本均值 x帽 =80，则80就是θ 的估计值

5.1.1点估计：用样本的估计量的某个取值直接作为总体参数的估计值。点估计量的可靠性是由它的抽样标准误差来衡量，表明一个具体的点估计值无法给出估计的可靠性的度量。

5.1.2区间估计

区间估计：在点估计的基础上，给出总体参数估计的一个区间 范围，该区间由样本统计量加减估计误差而得到。能够对样本统计量与总体参数的接近程度给出一个概率度量。

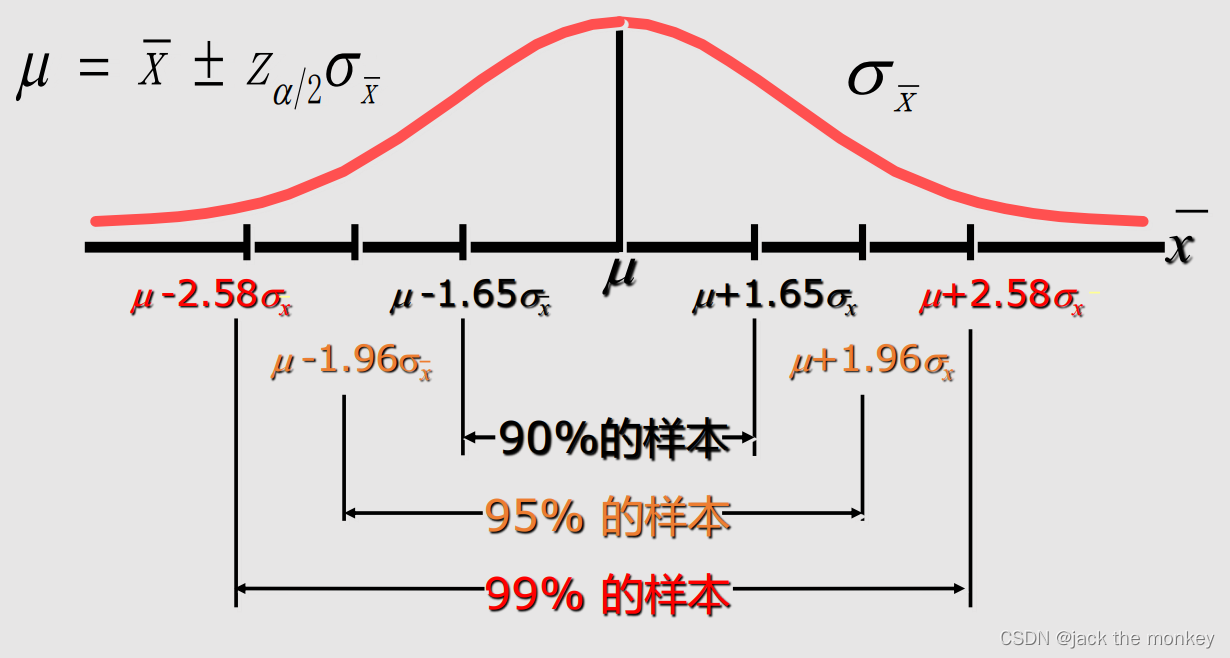
5.1.3置信水平

将构造置信区间的步骤重复很多次，置信区间包 含总体参数真值的次数所占的比例称为置信水平

表示为：(1-α)% 。其中α（显著性水平）是总体参数未在区间内的比例

常用的置信水平值有 99%, 95%, 90% 。相应的 α 为0.01，0.05，0.10。

5.1.4置信区间

由样本统计量所构造的总体参数的估计区间称为置信区间

总体参数以一定的概率落在这一区间的表述是错误的

5.2 评价估计量的标准

①无偏性(unbiasedness)：估计量抽样分布的数学期望等于被估计的总体参数。即无偏性的直观意义是样本估计量的数值在参数的真值附近摆动，且无系统误差。表现为这些估计量的平均值等于未知参数的真值。

②有效性(efficiency)：对同一总体参数的两个无偏点估计 量，有更小标准差的估计量更有效

③一致性(consistency)：随着样本量的增大，估计量的值越来越接近被估计的总体参数

5.3 点估计的应用

5.3.1点估计问题的提法