typora-copy-images-to: Risk and institurion
文章目录
Risk management and Financial Institutions —— Valuation and Scenario Analysis
-
Valuation:calculating the expected values (i.e., average values) of the future cash flows across all alternative outcomes and discounting the expected values back to today,预期现金流价值贴现
-
Scenario Analysis,a financial institution is interested in exploring the full range of situations that might exist at a particular future time
-
Valuation——what happen onaverage,Scenario analysis focus on extreme outcoms
7.1 Volatility and Asset Price

- 资产期末价格St服从lognormal正态分布,那么In St就服从正态分布
- 逗号前为此正态分布的均值,逗号后是该资产的方差

- 期末资产价格小于V的概率等同于In St小于In V的概率
- N 代表了累积正态分布函数,Excel 中未NORMSDIST,

-
图7.3表示了期末资产价格大于V的概率等同于In St大于In V的概率
-
d2的表达式:

-
已知N(d2)= q求V,则:

7.2 Risk-Neutral Valuation 风险中性定价
-
衍生品定价最重要的就是风险中性定价
-
风险中性世界的定义是投资者对承受的风险不要求回报的理想世界
-
因此任何的预期回报都应该是无风险收益率
-
我们可以对任何衍生品通过风险中性来定价
-
我们以底层资产的价格来为衍生品定价,风险上升,要求更多回报,底层资产价格下跌,相反的,风险下降,不能要求更多回报,底层资产价格上升
-
风险中性的估值意味着,将底层资产价格转换为衍生品价值的公式是独立与投资者的风险偏好的
-
风险中性世界,所有未来的预期现金流都以无风险利率贴现,简化了估值
- 简化后的步骤:
- 假定股票的预期平均收益在3%
- 计算call option 的预期payoff
- payoff贴现
- 简化后的步骤:
-
All we need to ask ourselves is: If we lived in a world where investors required an expected return equal to the risk-free rate on all investments, how would we value the derivative
-
当中性估值从中性世界到现实世界时,衍生品的预期收益与payoff的贴现率都会发生变化,而这样的变化往往正好相抵
7.2.1 Application to Forward Contract 远期合约的应用
-
long forward contract on no divident paying stock,dilivery price K,time to maturity is T
- 到期合约价值是St - K
- 中性定价理论指出,在 0 时间 远期合约的价值等于 T 时间的预期价值,并按照无风险利率贴现,公式如下:

-
股价的预期收益率在中性世界中为r,因此E(St) = S0erT
-
最终化简后,中性定价公式为:

7.2.2 Application to Binary Option 两值期权的风险中性定价应用
- 无红利的股价为30,有衍生品payoff 固定为100,条件是如果1年后股价大于40,上述称为binary option 或者 digital cash or nothing option ,risk free rate 3%,股价的增长率为10%,股价的波动率为30%
- 在风险中性世界,股价的预期增长率为3%,则μ= 0.03,T=1,σ=0.3,S0=30,V=40,把这些数据代入,求得期末价格大于40的概率 q

- 得出期末的预期收益为 100 * 0.1565 =15.65, 再以无风险利率贴现得到衍生品的定价为15.19
- 现实世界的股价以10%增长,得出payoff 为21.9,因此可以推算出现实世界的贴现率为36.6%

7.2.3 The Black-Scholes-Merton Application BSM公式的风险中性应用
- 条件:无红利股票的欧式期权,执行价格 K ,到期 T,无风险利率 r
- 则风险中性的期权价值为:

- 详情见Appendix E
7.2.4 Discrete Outcomes 离散的结果
-
风险中性定价可以在结果是离散的情况下使用
-
条件:π1 是payoff 为 1 的衍生品价值、π2 是payoff为1的衍生品价值,两者互斥完备,则有以下结论,到期一定会收到 payoff 1

- 普遍化,衍生品的价值为:

-
p1 和p2是风险中性世界中两个事件发生的概率
-
The result can be extended to the situation where there are many outcomes, The value of a derivative that pays Vi for outcome i (1 ⩽ i ⩽ n) is:

7.2.5 Application to Default Probabilities 违约概率的应用
-
信用衍生品的风险中性定价步骤:
- Estimating risk‐neutral default probabilities 估计风险中性违约概率
- 计算预期payoff
- 预期payoff 贴现
-
19章节会讲述,风险中性违约概率隐含在债券利率之中以及违约互换spreads中
7.3 Scenario Analysis 情景分析
-
应用于现实世界,并非风险中性世界
-
Moving between the real world and the risk-neutral world is simplified by a result known as Girsanov’s theorem
-
这个理论证明了,当风险偏好从中性世界转移到真实世界的时候,预期增长率会变化,但是波动率不变
-
例如:股票 real world 8% 增长 ,S0 = 30 ,σ = 0.25


-
假设q = 0.05 套用公式得出 V = 20.88 百分之95的概率损失不会超过30 -20.88
-
假设q = 0.01 套用公式得出 V = 17.16 百分之99的概率损失不会超过30-17.61
-
其实以上的例子就是VaR
-
以上就是现实的情景分析,而不是中性估值
7.4 When Both Worlds Have to Be Used 两个世界都使用的时候
- 现实世界设定情景,风险中性来定交易价格
- 比如,2年的远期合约,约定到期销售1m股票,50元的现价,55元的执行价,3%的无风险利率,10%的预期增长,波动率为30%,估计该组合6个月后的情景分析步骤:
- 6个月后股价的概率分布
- 用风险中性定价为6个月后的合约价值进行计算,合约价值也同样是概率分布的
- 依据自身评估需要,切分概率分布

- the worst‐case stock price was calculated in the real world,The forward contract was then valued for this worst‐case outcome using risk‐neutral valuation计算最坏股价的时候用的是现实世界的预期收益率,而在贴现计算远期合同价值的时候,使用的是风险中性定价
7.5 The Calculations in Practice
-
It is necessary to generate many scenarios for what might happen in the real world between today and the horizon date and then value the portfolio for each of these scenarios
-
计算股价、股指、汇率适用的普遍模型,假定预期增长率μ以及波动率σ是常数,或者是一个时间函数,那么得到以下模型:


-
δt的时间间隔来模拟市场变量
-
计算短期利率、波动率、商品价格适用更复杂的模型,因为volatility不固定,但是长期平均趋势被假定,我们把这种现象称之为均值回归
-
不同的市场变量并不一定是独立的,变量之间的相关关系依靠历史数据获得。这些相关关系又反应在ε之中
-
情景分析耗时耗力,需要的计算力极为巨大,蒙特卡罗模拟的实验次数必须被限定
7.6 Estimating Real-World Processes
-
情景分析的主要问题在于,我们在风险中性世界获知的信息要比在现实世界中多
-
现实中,预期回报的计算需要的历史数据远远大于计算波动率的历史数据
-
得到预期回报的一种方式是利用CAPM模型,步骤:
- 计算股票与指数标普500的ρ,计算出β

- 股票的波动率和市场波动率都要计算得出
- 现实世界的预期收益率通过CAPM获得
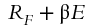
- 计算股票与指数标普500的ρ,计算出β
-
lambda = ρ / σM * E λ 意味着风险的市场定价,E is the expected excess return of the market over the risk‐free rate









 本文探讨了金融衍生品的估值方法,包括风险中性定价及其在不同金融工具中的应用,如远期合约、二元期权等。此外,还介绍了情景分析在评估极端市场状况下的作用。
本文探讨了金融衍生品的估值方法,包括风险中性定价及其在不同金融工具中的应用,如远期合约、二元期权等。此外,还介绍了情景分析在评估极端市场状况下的作用。
















 1352
1352

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








