typora-copy-images-to: Khan Academy
文章目录
-
- @[toc] Khan Academy
- Chapter 2 —— Vectors
- Vector Basis
- Equivalent Vectors
- Components of vectors
- Magnitude of Vectors
- Scalar multiplication
- Adding and subtracting vectors
- Graphically Adding and subtracting vectors
- Practice :Graphically adding and subtracting vectors
- Adding vectors algebraically & graphically
- Combined vector operations
- Vector operations review
- Unit vectors intro
- Worked example: finding unit vector with given direction
- Worked example: Scaling unit vectors
- Direction of vectors from components: 1st & 2nd quadrants
- Direction of vectors from components: 3rd & 4th quadrants
- Vectors forms review
- Vector components from magnitude & direction
- Vector components from magnitude & direction (advanced)
- Vector magnitude and direction review
Khan Academy
文章目录
- @[toc] Khan Academy
- Chapter 2 —— Vectors
- Vector Basis
- Equivalent Vectors
- Components of vectors
- Magnitude of Vectors
- Scalar multiplication
- Adding and subtracting vectors
- Graphically Adding and subtracting vectors
- Practice :Graphically adding and subtracting vectors
- Adding vectors algebraically & graphically
- Combined vector operations
- Vector operations review
- Unit vectors intro
- Worked example: finding unit vector with given direction
- Worked example: Scaling unit vectors
- Direction of vectors from components: 1st & 2nd quadrants
- Direction of vectors from components: 3rd & 4th quadrants
- Vectors forms review
- Vector components from magnitude & direction
- Vector components from magnitude & direction (advanced)
- Vector magnitude and direction review
Chapter 2 —— Vectors
Vector Basis

- A vector is a quantity that can be described as having both magnitude and direction
Equivalent Vectors

Components of vectors


Magnitude of Vectors
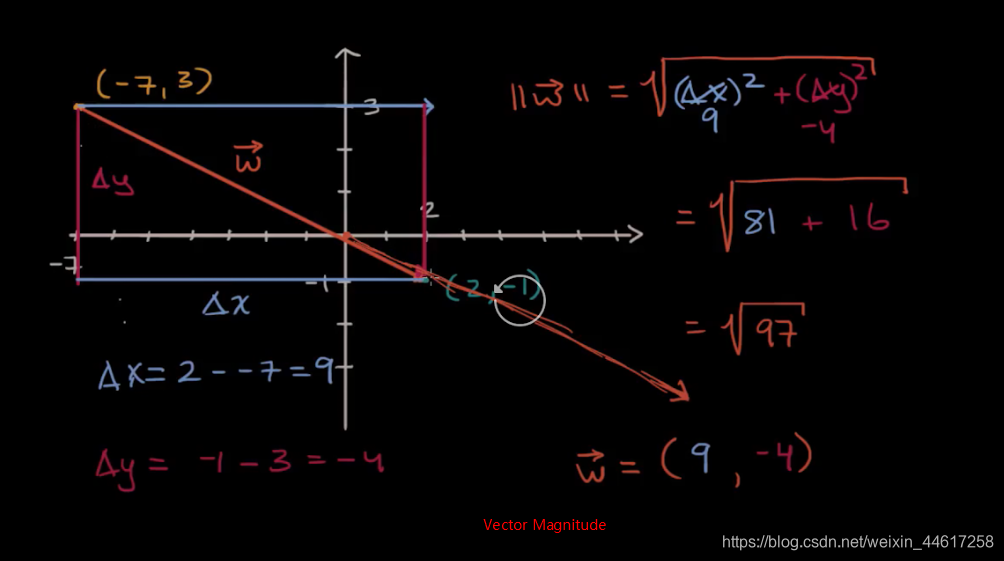
Scalar multiplication


Adding and subtracting vectors
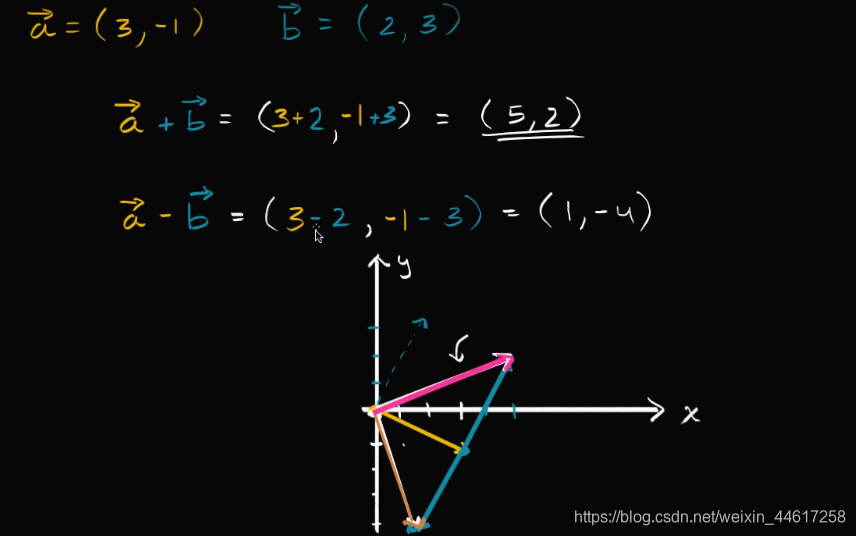
Graphically Adding and subtracting vectors

Practice :Graphically adding and subtracting vectors

Adding vectors algebraically & graphically
To add the vectors (x₁,y₁) and (x₂,y₂), we add the corresponding components from each vector: (x₁+x₂,y₁+y₂). Here’s a concrete example: the sum of (2,4) and (1,5) is (2+1,4+5), which is (3,9). There’s also a nice graphical way to add vectors, and the two ways will always result in the same vector…

Combined vector operations
Watch Sal find new vector 3u + 1/5w when u = (2, -1) and w = (-5, 5).

Vector operations review

Unit vectors intro
Unit vectors are vectors whose magnitude is exactly 1 unit. They are very useful for different reasons. Specifically, the unit vectors [0,1] and [1,0] can form together any other vector

Worked example: finding unit vector with given direction


Worked example: Scaling unit vectors
Watch Sal scale up a unit vector to have a magnitude greater than 1
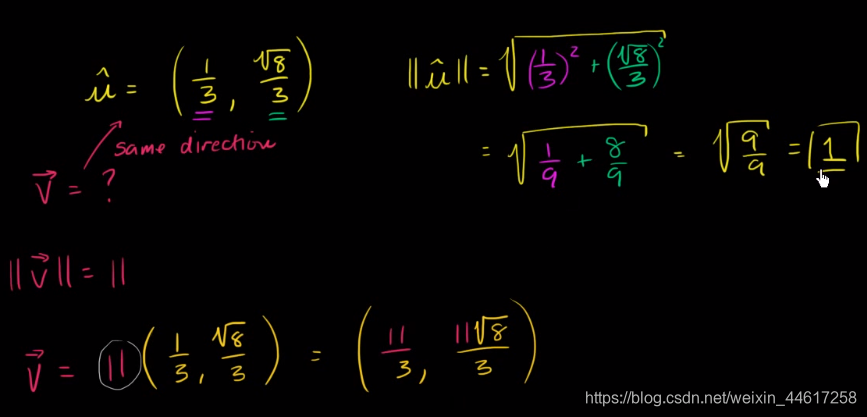
Direction of vectors from components: 1st & 2nd quadrants
Sal first finds the direction angle of a vector in the first quadrant, then moves onto a trickier one in the second quadrant
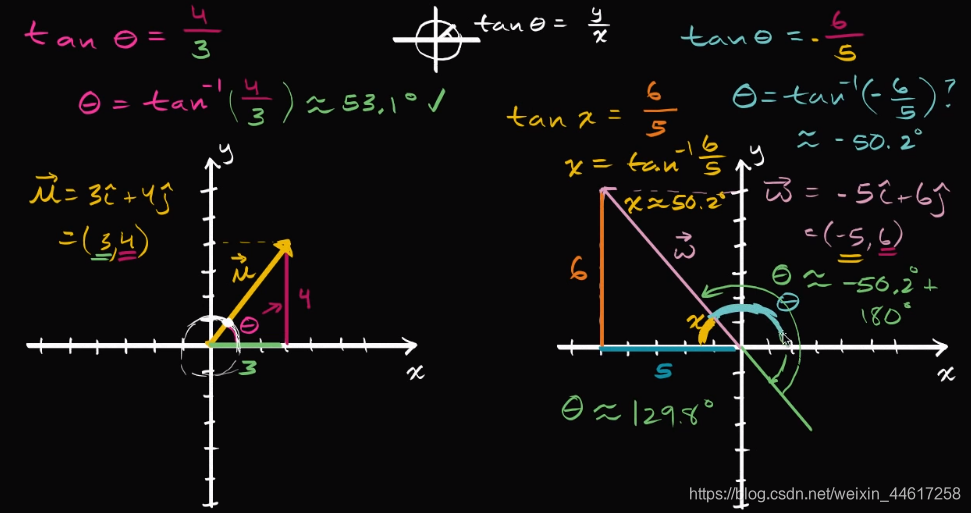
Direction of vectors from components: 3rd & 4th quadrants
Sal finds the direction angle of a vector in the third quadrant and a vector in the fourth quadrant



Vectors forms review

Vector components from magnitude & direction

practice:

Vector components from magnitude & direction (advanced)
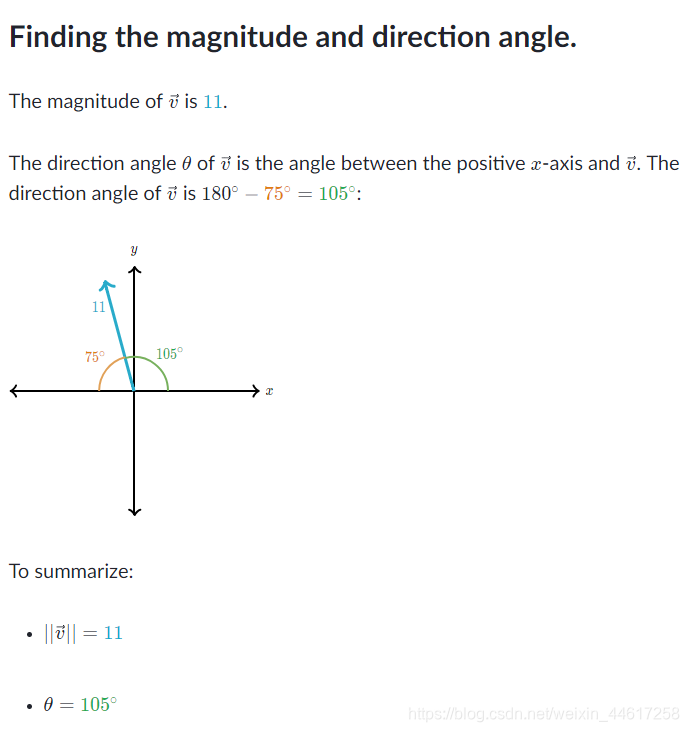

Vector magnitude and direction review










 本文深入探讨向量的概念,包括向量的基础、等效向量、向量的分量、向量的大小、标量乘法、向量加减法的代数与几何方法。同时,讲解了单位向量、向量方向的确定以及向量的综合运算。
本文深入探讨向量的概念,包括向量的基础、等效向量、向量的分量、向量的大小、标量乘法、向量加减法的代数与几何方法。同时,讲解了单位向量、向量方向的确定以及向量的综合运算。
















 9248
9248

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








