第二章 矩阵和数组
2.1. 矩阵的创建和组合
matlab就是矩阵实验室的缩写,可见其优势
2.1.0. 矩阵的定义



创建矩阵的一些实例



2.1.1. 关于向量有话说

2.1.1.1.向量的生成
(1)直接输入法:
直接在命令行之中输入,但是相应的格式有要求:
1)向量元素要用[]括起来;
2)元素之间可以用空格,逗号,或者分号隔开;

(2)冒号法:
基本格式是:x=first:increment:last
表示创建一个从first开始,到last结束,数据元素增量为increment的向量;
如果增量为1,可以简写为:x=first:last;

(3)利用函数linspace创建向量:
此函数会直接定义数据元素的个数,而不是定义数据元素之间的增量;
调用格式如下:linspace(first_value,last_value,number)
(4)利用函数logspace创建一个对数分隔的向量

2.1.1.2. 向量元素的引用


2.1.1.3. 向量的运算
(1).向量的四则运算:
向量的四则运算与数值的四则运算相同,相当于把向量之中的元素拆开,分别进行加减乘除运算,再将所得的结果组合成向量;
(2).向量的点积运算:
在MATLAB之中,对于向量a,b,点积可以利用a.*b得到,也可以直接用命令dot算出,命令的调用格式如下:
1)dot(a,b):返回向量a和b的点积,a,b需要是同维的,
2)dot(a,b,dim):返回向量a和b在dim维的点积;

(3).向量的叉乘运算
在解析几何之中,向量的叉乘结果是一个过两个相交向量交点且垂直于两向量所在平面的向量,在MATLAB之中,向量的叉乘运算可以由函数cross实现
1)cross(a,b):返回向量a和b叉乘,a,b必须是三维的向量
2)cross(a,b,dim):返回向量a,b在dim维的叉乘,需要注意的是a,必须有相同的维数;

(4).向量的混合积运算
可由两个函数(dot,cross)共同实现,
如下计算的是a点乘(b叉乘c)

2.2. 矩阵的生成
2.2.1. 创建简单矩阵
(1)单个标量的输入示例

(2)创建单行矩阵

规定步长
(3)创建多行多列矩阵

2.2.2. 常见矩阵的生成
(1)利用M文件创建


(2)利用文本创建

2.2.3. 创建特殊矩阵

(1)常用特殊矩阵的创建函数

用户可以直接用函数来生成某些特定的矩阵,常用的函数如下:
1)eye(n):创建n*n单位矩阵;
2)eye(m,n):创建m*n单位矩阵;
3)eye(size(A)):创建与A同类型的矩阵;
4)ones(n):创建一个n*n全一矩阵;
5)ones(m,n),ones(size(A))都是相似的;
6)zero(m,n),zero(n),zero(size(A))创建全0阵;
7)rand(n):在【0,1】区间上创建一个n*n均匀分布的随机矩阵,是随机生成的;
等等等等,还有很多......
(2)关于生成随机数

2.2.4. 矩阵的合并


2.3. 矩阵的寻访和赋值
2.3.1. 矩阵的寻访
有三种寻访方式:全下标,单下标,逻辑1标识,常用全下标,此处不再细说
2.3.2. 矩阵的赋值
知道了如何寻访,矩阵的赋值就很自然,举个例子说明就好了。


2.4. 进行矩阵运算的常用函数
2.4.1. 函数数组运算规则的定义
函数的数组运算是将函数作用于矩阵中的每一个元素,并将最后的结果存储为与原矩阵行列数相同的矩阵
2.4.2. 进行数组运算的常用函数
(1)常用数学函数


注意,这里面的众多函数,不仅仅适用于一个一个数,同时也是用于向量和数组,以及矩阵
(2)常用的三角函数
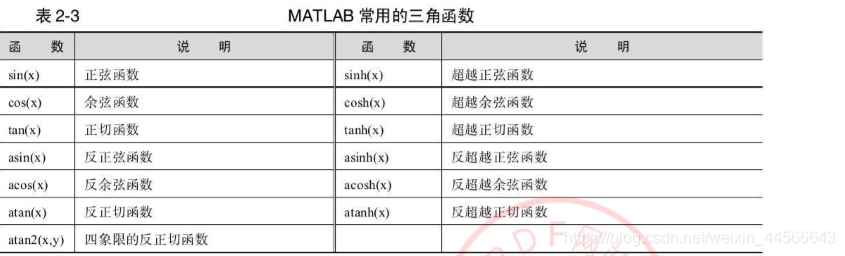
(3)适用于向量的常用函数
 (4)矩阵的加法运算
(4)矩阵的加法运算

(5)矩阵的乘法运算
-
(1)数乘运算

-
(2)乘运算



-
(3)点乘运算


(6)矩阵的除法运算
计算左除A\B的时候,A的行数要与B的行数一致
计算右除A/B的时候,A的列数要与B的列数一致 -
左除运算


-
右除运算

2.5. 查询矩阵信息
在矩阵的使用过程中,经常需要查询某个矩阵的一些基本信息,比如行数,列数,总元素个数,元素数据类型等等
2.5.1. 矩阵的形状信息


2.5.2. 矩阵的数据类型

2.5.3. 矩阵的数据结构

2.6. 数组运算与矩阵运算
矩阵和数组在一般情况下是没有区别的,。严格来说的话,一个矩阵就是一个二维的数组


本部分会介绍一些矩阵的基本运算,矩阵的基本运算包括:加,减,乘,数乘,点乘,乘方,左除,右除,求逆。
注意:左除,右除/
例:A*X=B解就是X=A\B,(因为A在左面)
在MATLAB中的矩阵运算的维数要求与线性代数是一致的;
(1)矩阵的加法运算

(2)矩阵的乘法运算
-
(1)数乘运算

-
(2)乘运算



-
(3)点乘运算


(3)矩阵的除法运算
计算左除A\B的时候,A的行数要与B的行数一致
计算右除A/B的时候,A的列数要与B的列数一致 -
左除运算


-
右除运算

(4)幂函数



(
2.5. 查询矩阵信息
(1)矩阵的扩展
很简单,根据需要来看,需要多大就是多大


(2)矩阵元素的删除
通过将行或列或指定元素指定为空矩阵【】,即可从矩阵中删除元素。

2.7.2. 矩阵的重构

Rot90(A):将矩阵A逆时针旋转90度;
Rot90(A,k):将矩阵A逆时针方向旋转90*k度,K为正整数或者负整数;
还有很多翻转命令;
fliplr(X):将X左右翻转;
flipud(X):将X上下翻转;
flipdim(X,dim):当dim为1时对行翻转,为2时对列翻转;矩阵的抽取
主要是指对对角元素和上下三角阵的抽取:
1)diag(X,k),抽取矩阵X的第k条对角线上的元素向量,k为0时抽取主对角线元素,k为正整数时抽取上方第k条对角线的元素;k为负整数时抽取下方第k条对角线的内容
2)diag(X)抽取主对角线元素;
3)tril(X):抽取矩阵X的主下三角部分;
4)tril(X,k):抽取矩阵X第k条对角线下面的部分(注意包括第k条对角线);
5)triu(X,k);抽取矩阵X第k条对角线上面的部分(注意包括第k条对角线);举例说明


矩阵部分元素的提取

2.8. 稀疏矩阵
稀疏矩阵是一种特殊类型的矩阵,矩阵中含有较多的零元素,matlab可以只保留致谢非零元素在矩阵中的位置,计算时减少计算时间。
2.8.1. 稀疏矩阵的存储方式

2.8.2. 稀疏矩阵的创建


2.9. 多维数组
在实际应用中,经常要构造多于二维的数组,我们将多于二维的数组统称为多维数组
对于三维数组,第一维是行,第二维是列,第三维是页
2.9.1. 多维数组的创建
多维数组的创建有以下四种方法:

(1)利用全下标元素赋值方式创建多维数组,

(2)由大小相等的二维数组组合成三维数组


(3)由特殊函数直接创建一个三维数组




2.10. 多项式的表达式及其操作

2.10.1. 多项式的表达式和创建
1)对于带字符多项式
基本方法是直接输入例:a倍的x的n次方加b倍的x的n-1次方

2)对于带数值多项式
最简单的方法就是直接输入向量,通过函数来实现;
调用格式:poly2sym§其中p为多项式的系数向量;

2.10.2. 多项式运算函数
2.10.2.1. 常见多项式运算函数

2.10.2.2. 数值多项式的四则运算:
MATLAB没有专门提供针对多项式加减运算的函数,多项式的加减运算实际上是多项式对应系数的加减运算,
注意:相加减的两个向量必须阶次相同,阶次不同的时候,必须要低阶多项式用0填补,使其与高阶多项式拥有相同的阶次,这样才可以加减运算,
1.乘法运算:
多项式的乘法用函数conv(p1,p2)来实现,相当于执行两个数组的卷积;

注意:多项式的四则运算本质上式对应系数的四则运算。
2.除法运算
多项式的除法运算使用deconv(p1,p2)函数来实现,相当于执行两个数组的解卷
调用格式如下:【k,r】=deconv(p,q)
k返回的是多项式p除以q的商,r是余式
注意:[k,r]=deconv(p,q)<=>p=conv(q,k)+r;


2.10.2.3. 多项式导数运算

2.11. 特殊变量
本节介绍的特殊变量包括单元型变量和结构型变量。这两种数据类型的特点是允许用户将不同但是相关的数据类型继承一个单一的变量,方便数据的管理
2.11.1. 单元型变量
单元型变量是以单元为元素的数组,每一个元素称为单元,每一个单元可以包含其他类型的数组,实数矩阵,字符串,复数向量等
2.11.1.1. 单元型变量的创建
单元型变量的定义有两种方式:
- (1)赋值语句直接定义
- (2)由cell函数预先分配存储空间,然后再对单元元素逐个赋值
(1)赋值语句直接定义
在直接赋值语句中,与在矩阵的定义中使用中括号不同,单元型变量的定义需要使用大括号,而且元素之间要用逗号隔开
 (2)对单元的元素逐个赋值
(2)对单元的元素逐个赋值
这种方法的操作方式就是先预先分配好单元型变量的存储空间,然后再对变量中的元素进行逐个赋值
实现预分配存储空间的函数时cell()

2.11.1.2. 单元型变量的引用
单元型变量的引用应当用大括号作为下标的标识,而小括号作为下标标识符则只显示该元素的压缩形式

2.11.1.3.matlab语言中有关单元型变量的函数


2.11.2. 结构型变量
2.11.2.1. 结构型变量的创建和引用
结构体变量是根据属性名(filed)组织起来的不同数据类型的集合,结构的任何一个属性可以包含不同的数据类型
结构体变量用函数struct()来创建


2.11.2.2. 结构型变量的相关函数









 本文深入探讨了MATLAB中的矩阵和数组操作,包括矩阵的创建、组合、运算及信息查询,向量生成与运算,特殊矩阵生成,矩阵重构,稀疏矩阵处理,多维数组创建,以及多项式表达与操作。同时介绍了单元型和结构型变量的使用。
本文深入探讨了MATLAB中的矩阵和数组操作,包括矩阵的创建、组合、运算及信息查询,向量生成与运算,特殊矩阵生成,矩阵重构,稀疏矩阵处理,多维数组创建,以及多项式表达与操作。同时介绍了单元型和结构型变量的使用。
















 966
966

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








