Why least squares so powerful?

考虑到翻译会有不严谨的地方，很多地方我直接使用英语描述。

1. Residual Distribution

• 通常，我们使用Generalized Gauss-Markov假设。假设输出变量的残差都是zero-mean，服从高斯分布，同时他们之间的关系使用covariance matrix表示（对角线是变量的variance，非对角线则表示了不同变量之间的纠缠关系）。
• 但是明显的是，这样的假设并不一定是正确的。我们面临的可能是非高斯的分布。

在下面我们会看到：

• 对高斯误差的优化，其实是最小二乘优化。
• 对非高斯误差的优化，也可以使用最小二乘获得很好的近似。

2. 不同噪音下线性系统的ML

下面我们分别考虑不同的噪音影响下的，Maximum likelihood estimation的不同形式。
我们列举了高斯噪音，拉普拉斯噪音以及均匀分布噪音。

考虑高斯噪音下的线性系统：
linear measurement model：
matrix form:
$$Y=AX+\nu$$

component form:
$$y_i=a_i^{T}x+{\nu }_i$$

2.1 Maximum likelihood Esimation

对系统，我们优化Maximum log likelihood ：

$$maximize(overx)\log p_x(y)$$

$$maximize(overx)l(x)=\sum _{i=1}^m\log p(y_i-a_i^{T}x)$$

这实际上是一个对penality的优化，penality则是噪音的分布。

2.2 Gaussian noise

考虑高斯噪音 $\mathcal{N}(0,{\sigma }^2)$：

$$p(z)=(2\pi {\sigma }^2{)}^{-1/2}\exp (-z^2/(2{\sigma }^2))$$

那么我们的优化目标函数就变为了：

$$l(x)=-\frac{m}{2}\log (2\pi {\sigma }^2)-\frac{1}{2{\sigma }^2}\sum _{i=1}^m(a_i^{T}x-y_i{)}^2$$

第一项与优化参数x无关，我们只需要考虑上面的第二项，而它则是一个$l_2$范数：最小二乘（least square）。
但是其他的噪音假设会得到什么样的结果呢？我们来考量几个其他的假设。

2.3 Laplacian noise

考虑拉普拉斯噪音：

$$p(z)=\frac{1}{2a}\exp (-\frac{|z|}{a})$$

$$l(x)=-m\log (2a)-\frac{1}{a}\sum _{i=1}^m|a_i^{T}x-y_i|$$

ML的优化其实是对$l_1$范数的优化。

2.4 Unifrom noise

考虑误差均匀分布在$[-a,a]$：

$$l(x)=\{\begin{array}{ll}-m\log (2a)& |a_i^{T}x-y_i|\le a,i=1,..,m\\ -\inf & otherwise\end{array}$$

2.5 Summary

• Least-squares is exactly maximum likelihood estimation under the assumption that the noises are gaussian!
• 但是其他的噪音假设，会导致不同的优化目标函数的表达式。
• 那我们还能不能（几乎）“无脑”得使用最小二乘优化呢？或者说最小二乘是不是比我们想象中得更强大呢？

下面会介绍凸包的一些定理，以展现最小二乘的强大。

3. convex optimization

3.1 convex set

在这里不需要凸优化的过多概念，只需要知道凸函数就足够继续了。

Definition:
for $x_1,x_2\in A$, we say $A$ is a convex set if and only if the following holds for any $\theta \in [0,1]$:
$$\theta x_1+(1-\theta )x_2\in A$$

3.2 Minimum volume ellipsoid around a set

Lowner-John ellipsoid for a set C minimum volume ellipsoid $\mathcal{E}$ such that $C\subseteq \mathcal{E}$

我们考虑一个特殊的例子来证明：



优化问题可以写成：

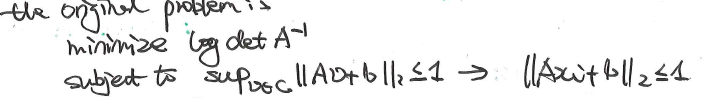
3.3 rewrite constraints

通过一个简单的变化，我们重写原本的约束函数：

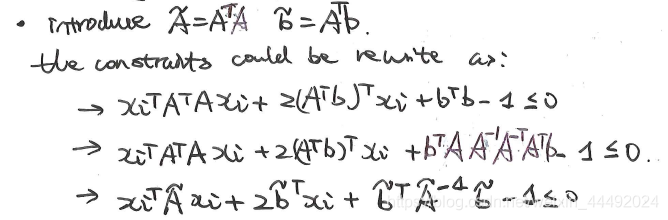
3.4 KKT condition

这个是和凸优化duality相关的特性。具体的话，可以参考convex optimization的课程和教材。
简单来说的话：

• 如果一个凸优化问题有strong dualtiy。
• 那么我们可以通过求解dual problem，来求解原本的问题。
• strong duality的条件之一是KKT condition。
• KKT condition由四个类组成（下面是当前问题的KKT condition）

我们可以（不正式地）理解为由于我们问题的凸函数特征，下面的几个条件是一定满足的。

上面的几个条件的表达明显很复杂，不够幸运的是，我们可以通过一些线性的坐标系变化得到简答的表达式。坐标系变换的例子图示如下：


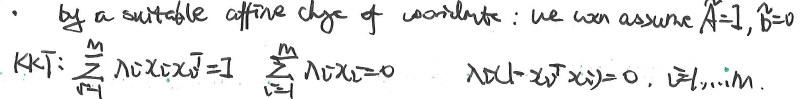
另外，通过上面的条件，我们可以得到：

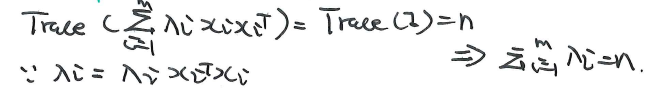
3.5 1/n scale the ellipsoid

我们考虑缩放LJ椭圆，使用一个缩放尺度1/n。然后我们考虑这个新的缩小的椭圆内的元素：

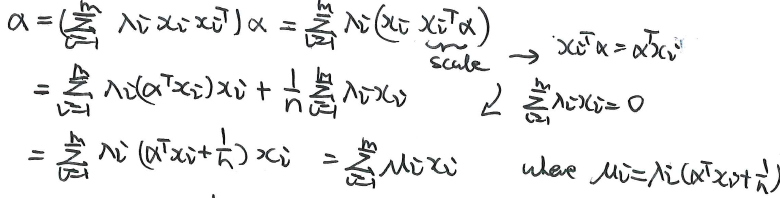
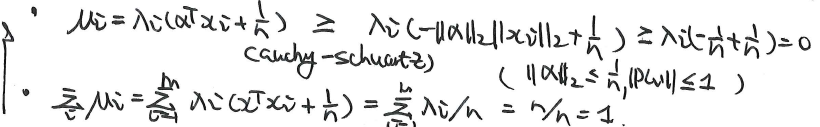
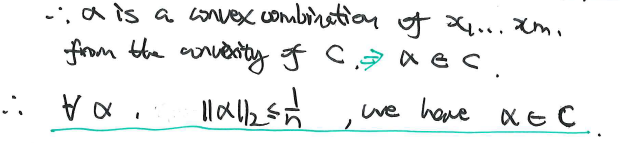
在这里我们证明了，任意新的缩小椭圆内的元素，都属于原本的凸集C。也就是说，这个缩小的椭圆是严格在C集合内部的。

上图来自《convex optimization》page 412。

3.6 for symmetric set

在C是对称集合的情况下，这个缩放因子还能进一步被控制为$\sqrt{n}$。

4. 其他范数

下文来自《convex optimization》page 412-413。


对于这个结论，我们可以有以下几个非常好的描述：

• Ellipsoides are universal approximations of convex sets.

• Any norm on ${\mathcal{R}}^n$，can be approximated by a quadratic norm, with a factor of $\sqrt{n}$

• Any sysmetric convex set can be approximated by an ellipsoid within a factor $\sqrt{n}$

• LJ“椭圆”是所有对称凸集的在scale为$\sqrt{n}$下的近似。

• L2是其他所有模在$\sqrt{n}$下的近似。

总得来说：

• 如果我们假设高斯噪音，那么最小二乘是最合适的范数选择。
• 但是哪怕假设不成立，无论实际是什么样的误差，应该选取什么样的范数。最小二乘都可以取得一个很好的近似。

也就是说，当然高斯假设下用最小二乘是最好的。但是无论你是什么噪音模型，使用最小二乘都可以得到很好的结果！