洛谷 P1579 哥德巴赫猜想（升级版）

最新推荐文章于 2023-10-05 14:14:20 发布

原创最新推荐文章于 2023-10-05 14:14:20 发布 · 131 阅读

0 ·

CC 4.0 BY-SA版权

洛谷专栏收录该内容

56 篇文章

订阅专栏

本文深入探讨了三种高效求解素数的方法：常规判断、埃拉托斯特尼筛法及线性筛法（欧拉筛法）。通过实例展示，解析每种方法的实现原理与代码细节，帮助读者理解并掌握不同场景下最优的素数求解策略。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

在这里插入图片描述
易错样例：
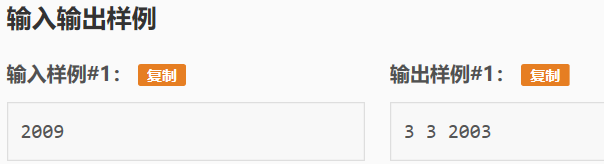
输入：17079
输出：3 23 17053

常规isPrime函数：

#include<bits/stdc++.h>
using namespace std;
int isPrime(int n)//判断素数
{
 if (n <= 1)return 0;
 for (int i = 2; i <= sqrt(n); i++)
  if (n%i == 0)
   return 0;
 return 1;
}
int main()
{
 int n,i,j,k; cin >> n;
 for (i = 2; i < n; i++)//节省时间只写两层循环
  for (j = 2; j < n; j++)
   if (isPrime(i) + isPrime(j) + isPrime(n - i - j) == 3)//利用isPrime函数的返回值判断三个数全为素数
   {cout << i << " " << j << " " << n - i - j << endl;exit(0);}//输出后直接结束程序
 return 0;
}

用埃拉托斯特尼筛法：

#include<bits/stdc++.h>
using namespace std;
const int SIZE = 1000000;
int prime[SIZE], check[SIZE];//全局变量自动赋零，零为素数
void isPrime()//使用埃拉托斯特尼筛法。
{
 int i, j;
 int pos = 0;
 for (i = 2; i < SIZE; i++)
 {
  if (!check[i])prime[pos++] = i;//如果是素数，记录
  for (j = i * 2; j <1SIZE; j += i)check[j] = 1;//标记为合数
 }
}
int main()
{
 int n,i,j,k; cin >> n;
 isPrime();
 for (i = 0; i < n; i++)
  for (j = 0; j < n; j++)
   for (k = 0; k < n; k++)
    if (prime[i] + prime[j] + prime[k] == n)
    {cout << prime[i] << " " << prime[j] << " " << prime[k] << endl; exit(0);}
 return 0;
}

线性筛法（欧拉筛法）：

#include<bits/stdc++.h>
using namespace std;
const int SIZE = 1000000;
int prime[SIZE], check[SIZE];//全局变量自动赋零，零为素数
void isPrime()//线性筛法
{
 int i, j;
 int pos = 0;
 for (int i = 2; i < SIZE; i++)
 {
  if (!check[i])prime[pos++] = i;//如果是素数，记录
  for (int j = 0; j < pos && i*prime[j] < SIZE; j++)
  {
   check[i*prime[j]] = 1;//筛掉
   if (i % prime[j] == 0)break;
  }
 }
}
int main()
{
 int n, i, j, k; cin >> n;
 isPrime();
 for (i = 0; i < n; i++)
  for (j = 0; j < n; j++)
   for (k = 0; k < n; k++)
    if (prime[i] + prime[j] + prime[k] == n)
    {cout << prime[i] << " " << prime[j] << " " << prime[k] << endl; exit(0);}
 return 0;
}