洛谷 P1028 数的计算

最新推荐文章于 2022-01-24 23:18:02 发布

Louis1874

最新推荐文章于 2022-01-24 23:18:02 发布

阅读量201

点赞数

CC 4.0 BY-SA版权

本文链接：https://blog.youkuaiyun.com/weixin_44413191/article/details/89819778

博客围绕找出具有特定性质数的个数展开，先给出题目描述，包括输入一个不超1000的自然数n，按规则处理。通过计算得出规律，给出两种代码，一种递归函数超时，另一种洛谷题解的循环递归节省了时间。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目描述
我们要求找出具有下列性质数的个数(包含输入的自然数nnn):
先输入一个自然数nnn(n≤1000n \le 1000n≤1000),然后对此自然数按照如下方法进行处理:

不作任何处理;

在它的左边加上一个自然数,但该自然数不能超过原数的一半;

加上数后,继续按此规则进行处理,直到不能再加自然数为止.

输入输出格式
输入格式：

111个自然数nnn(n≤1000n \le 1000n≤1000)
输出格式：

111个整数，表示具有该性质数的个数。
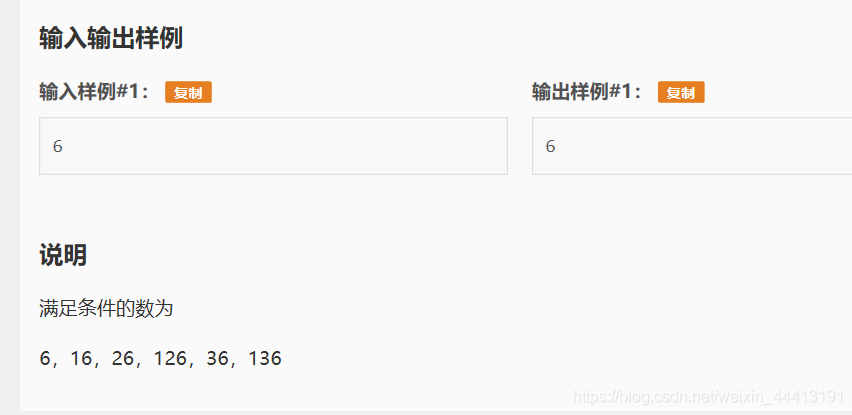
在这里插入图片描述
通过计算几个fn，得出规律：
n%20时
f(n)=f(n-1)+f(n/2)
n%21时
f(n)=f(n-1)
第一段代码使用递归函数，超时

#include<iostream>
using namespace std;
int func(int n)
{
 int fn = 1;
 if (n == 0||n==1)
  return fn;
 else
 {
  if (n % 2 == 0)
   fn = func(n - 1) + func(n / 2);
  else
   fn = func(n - 1);
 }
 return fn;
}
int main()
{
 int n;
 cin >> n;
 cout<<func(n)<<endl;
 return 0;
}

第二段代码来自洛谷题解，使用了循环递归

#include<iostream>
using namespace std;
int main()
{
 int n;
 cin >> n;
 int f[1000];
 f[0] = f[1] = 1;
 for (int i = 2; i <= n; i++)
 {
  if (i % 2 == 0)
   f[i] = f[i - 1] + f[i / 2];
  else
   f[i] = f[i - 1];
 }
 cout << f[n] << endl;
 return 0;
}