Kaplan-Meier生存曲线估计

0. 简介

生存分析（survival analysis）是生物医学研究中常用的分析方法。在队列随访研究中，我们会事先定义一些观察终点，比如肿瘤复发、患者死亡、血压达标等，这些终点称为事件（event）。从研究开始到发生事件的时间间隔称为生存时间（survival time），某些场景下也称为失效时间（failure time）。由于生存时间数据具有以下两个特点，所以提出生存分析这一特殊的分析方法：

（1）偏态分布：生存时间通常具有明显的偏态分布，有正态分布假设的统计方法不能适用。

（2）删失（censoring）：研究对象在观察时间内没有发生事件称为删失。一种情况是研究对象在中途失访或退出，导致没有观察到事件；另一种情况是超过了最长的随访时间事件仍未发生。删失数据是一种不完整数据，是生成分析独有的重要组成部分。

1. 生存曲线

在t检验或回归分析中，我们估计的是研究对象的一些参数，比如均值、标准差、回归系数等。而在生存分析中，我们得到的不是单个特定的数值，而是一条曲线，称为生存曲线（survival curve）。曲线对应的函数称为生存函数（survival function），用S(t)表示，其定义为：

S(t)是个体生存超过时间t的概率

以时间t为横坐标，S(t)为纵坐标，绘制出来的曲线就是生存曲线。生存曲线具有两个特点：

（1）显然，在观察开始的时候，所有个体都是存活的，所以S(t=0)=1；

（2）时间越长，生存的概率越小，所以S(t)是递减的。

2. S(t)的估计

接下来的问题是如何估计S(t)，这也是一切生存分析的前提。有多种方法可以估计生存函数，这里介绍一种常用的方法，适用于小样本的资料，即Kaplan-Meier法（简称KM法），也叫乘积极限法。它的思想其实很简单，就是将S(t)写成一个递推式。假设我们已经计算出了时间t1的生存函数值S(t1)，我们想要计算时间t2（t2>t1）的生存函数值，那么这个个体必须首先存活过时间t1，再从t1存活到t2，用公式表示：

S(t2) = Prob(从t1存活到t2）× S(t1)

其中，Prob表示概率。

那么如何计算从t1存活到t2的概率呢？一个简单的估计方法是：

Prob(从t1存活到t2） = 1 - d/n

其中d代表在t1到t2这段时间内，实际发生了事件的个体数；n代表在t1到t2这段时间内，有可能发生事件的个体总数（可以理解为在t1时刻仍然存活的个体总数）。显而易见，如果t1到t2这段时间内没有个体发生事件(d=0)，那么S(t)的值将保持不变。所以我们只需要在观察到发生了事件的时间点上，通过递推公式去更新S(t)的值。

这里唯一需要注意的是删除数据的处理。假设一个个体在第10年的时候发生了删失，但是如果他在第5年的时候发生了事件，我们也是有可能记录到的。因此，上面公式中的n包含了在该时间点以及该时间点以后删失的个体，而不包含在这之前删失的个体。

以上就是KM估计法所有的内容，具体实现也很容易，请看下面的例子。

3. 计算举例

下面以一个真实的研究案例来展示KM法的详细计算过程。数据集来自于一个淋巴瘤患者的生存时间研究（McKelvey et al., 1976, Cancer, 38, 1484-1493），数字代表患者生存的天数，*号代表数据删失：

6, 19, 32, 42, 42, 43*, 94, 126*, 169*, 207, 211*, 227*, 253, 255*, 270*, 310*, 316*, 335*, 346*

为了方便分析，对数据进行了从小到大排序，删失数据也包含其中。

表1展示了KM法的计算过程。

生存时间 (t)	发生事件个体数 (d)	t时刻仍存活个体数(n)	1-d/n	S(t)
0	-	19	-	1
6	1	19	0.9474	0.947
19	1	18	0.9444	0.895
32	1	17	0.9412	0.842
42	2	16	0.8750	0.737
94	1	13	0.9231	0.680
207	1	10	0.9000	0.612
253	1	7	0.8571	0.525

表1：KM估计法的详细计算过程

表1一共包含5列，最后两列可以通过前三列计算出来。第一列是生存时间t，注意不包含删失的时间，但包含时间0。第二列是t时刻事件发生个体数，可以看到大部分数据为1。第三列是t时刻仍然存活的个体数。

第一行中，即0时刻，所有个体均存活，S(0)=0。后面各行中，第一列和第二列都可以从原始数据中直接得出，第三列是通过上一行的第三列减去上一行的第二列得到。比如第三行，n=18=19（上一行的n）-1（上一行的d）。需要注意的是删失数据的处理。从上一行的生存时间开始（包含）到本行的生存时间（不包含）为止，这段时间内删失的个体数也要一并减去。所以我们可以看到，第六行中，不是16-2=14，而是16-2-1=13，因为有一个患者在第43天的时候发生了删失。

前三行准备好后，第四行就是一个简单的数学计算。除了第一行外，其余各行的第五列等于上一行的第五列乘以本行的第四列。

以第五列S(t)为纵坐标，第一列t为生坐标，就可以绘制生存曲线，如图1所示。读者可能注意到了，表格中的数据只是一些离散的点，但是生存曲线确是一个连续的折线图。这是因为我们将连续两个生存时间之间的函数值（生存概率）都人为设置成了前一个生存时间对应的函数值。

图1 KM生存曲线

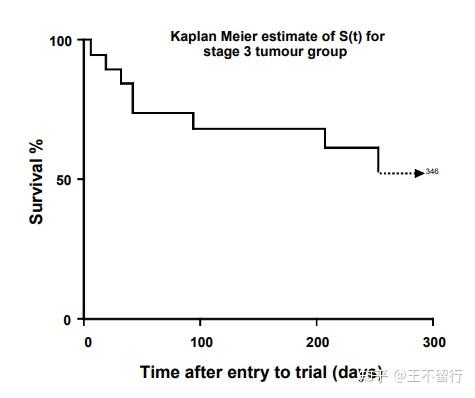
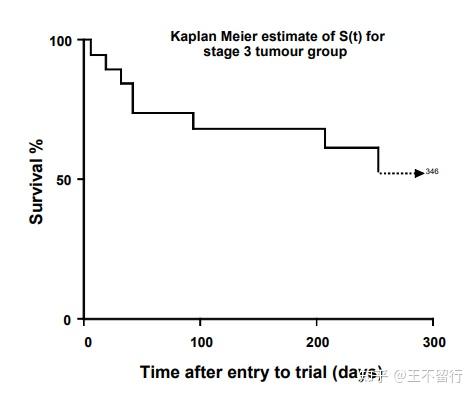
尽管数据中包含了大于253天的数据，但是都删失了。有的作者会画一条水平线延伸到最大的删失时间，而有的作者仅绘制到最大的事件发生时间。这里并没有统一的规定应该怎么做，一般说来，前者展示的信息更全面，但是如果删失的时间数值很大，可能会导致图表变形。

。