但不得不说的是Matlab只需五行代码就解决了~~matlab版的就放最下面了,没有对比就没有伤害,555
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
x_data = np.linspace(0, 1,11)
y_data = 0.5 + 0.4 * np.sin(2 * np.pi * x_data)+ np.random.normal(0.0, 0.05)
plt.scatter(x_data, y_data)
plt.show()
'''#一阶
W = tf.Variable(tf.random_uniform([1],-1.0,1.0),name='W')
b = tf.Variable(tf.zeros([1]))
y = W * x_data + b
'''
#三阶
W1 = tf.Variable(tf.random_uniform([1]))
W2 = tf.Variable(tf.random_uniform([1]))
W3 = tf.Variable(tf.random_uniform([1]))
b = tf.Variable(tf.zeros([1]))
y = W1 * x_data+W2 * np.multiply(x_data,x_data)+W3 *np.multiply( np.multiply(x_data,x_data),x_data) + b
'''#十一阶
W = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
for i in range(11):
W[i] = tf.Variable(tf.random_uniform([1]))
b = tf.Variable(tf.zeros([1]))
y = b
xx = x_data
for i in range(11):
y = y + W[i] * xx
xx = np.multiply(xx, x_data)
'''
loss = tf.reduce_mean(tf.square(y - y_data))
optimizer = tf.train.GradientDescentOptimizer(0.5)
train = optimizer.minimize(loss)
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
# 执行50000次训练
for step in range(50000):
sess.run(train)
W1, W2, W3, b = sess.run([W1, W2, W3, b])
plt.scatter(x_data, y_data)
plt.plot(x_data, W1 * x_data+W2 * np.multiply(x_data,x_data)+W3 *np.multiply( np.multiply(x_data,x_data),x_data) + b, c='r')
plt.show()
'''
W, b = sess.run([W, b])
plt.scatter(x_data,y_data,c='r')
#plt.plot(x_data,sess.run(W1)*x_data+sess.run(W1)*x_data*x_data+sess.run(W1)*x_data*x_data+sess.run(b))
plt.plot(x_data,x_data*W+b)
plt.show()
b = sess.run(b)
axx = x_data
for i in range(11):
b = b + sess.run(W[i]) * axx
axx = np.multiply(x_data, axx)
print(sess.run(W[i]))
plt.scatter(x_data, y_data, c='r')
plt.plot(x_data, b)
plt.show()
'''
输出结果:
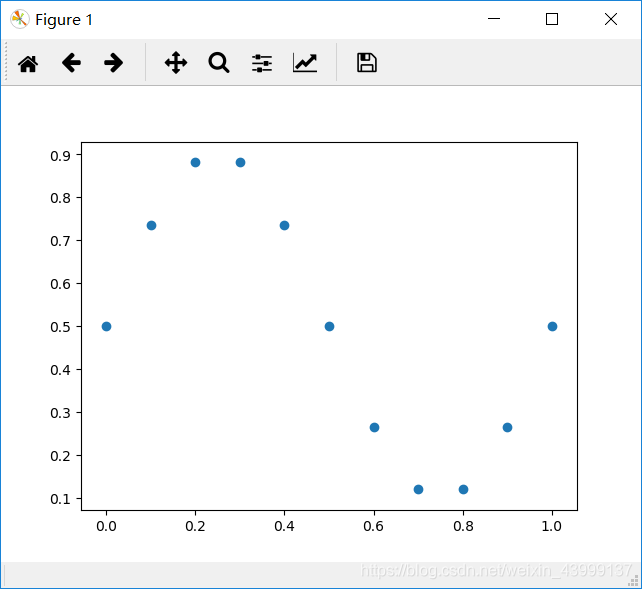
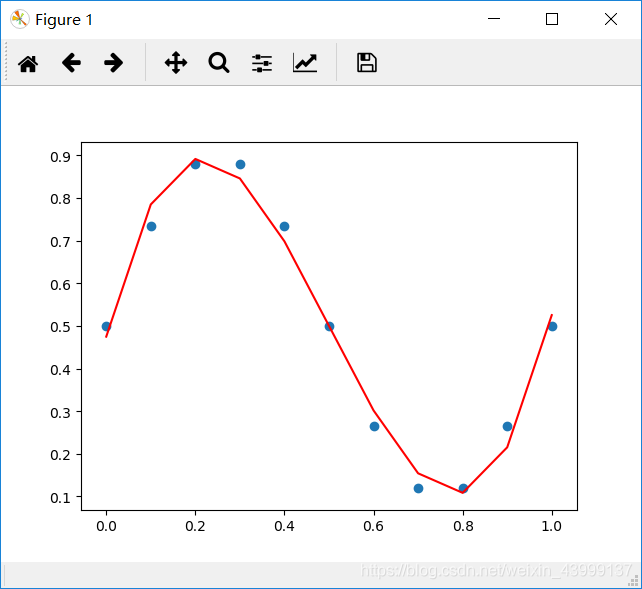
function train_30_3()
x=0:0.2:2;
y=0.5+0.4*sin(2*pi*x)+normrnd(0,0.05);
a=polyfit(x,y,1);
y1=polyval(a,x);
b=polyfit(x,y,3);
y2=polyval(b,x);
c=polyfit(x,y,11);
y3=polyval(c,x);
subplot(1,3,1),plot(x,y,'go',x,y1,'b--')
subplot(1,3,2),plot(x,y,'go',x,y2,'b--')
subplot(1,3,3),plot(x,y,'go',x,y3,'b--')
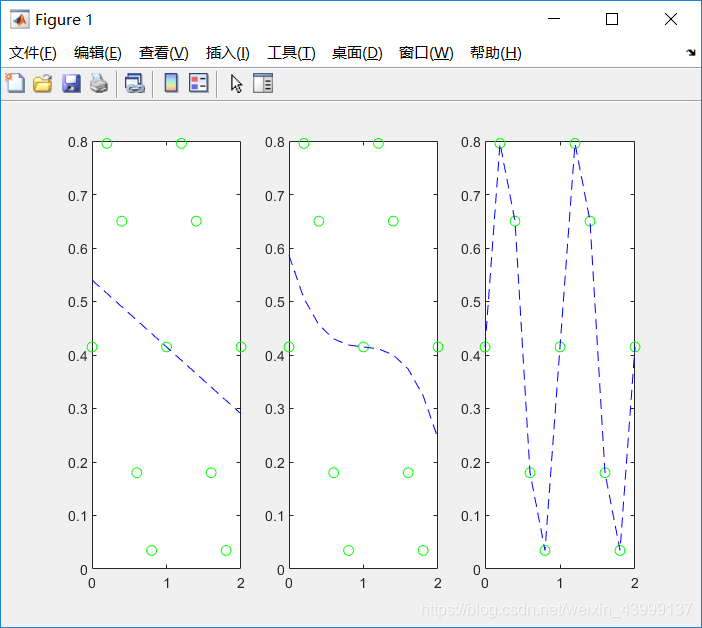





 本文通过使用TensorFlow进行一阶、三阶及十一阶多项式曲线拟合,对比了Matlab的实现效率。展示了如何用TensorFlow从头开始定义变量、计算损失并进行梯度下降优化,最终绘制出拟合曲线。
本文通过使用TensorFlow进行一阶、三阶及十一阶多项式曲线拟合,对比了Matlab的实现效率。展示了如何用TensorFlow从头开始定义变量、计算损失并进行梯度下降优化,最终绘制出拟合曲线。

















 633
633

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










