“函数空间”,“傅立叶级数”,“勒让德多项式”,“希尔伯特空间”我读大学都曾遇到过,我学的教材这些概念是直接给出定义,基本不可能理解。我在Gilbert Strang《线性代数及其应用》中看到了与函数空间有关的内容,篇幅不长,思维方式很清晰,直观。看完就觉得这些概念也并不是那么神秘,都是能够理解的。
本文的目的是把有限维矩阵向量空间的思想,扩展到无限维向量空间。并以傅立叶级数为例讨论。
无限维向量空间
假设3*3矩阵A的列向量线性无关,则矩阵A的列向量构成 R 3 R^3 R3空间。现在将线性无关组的向量个数推广到无穷大,即 R ∞ R^\infty R∞.
相关定义
对于
R
∞
R^\infty
R∞,需要有一定的限制条件,一个自然的想法是向量的长度为有限值。即
v
=
(
v
1
,
v
2
,
v
3
,
.
.
.
)
v=(v_1,v_2,v_3,...)
v=(v1,v2,v3,...)
的长度,无穷级数:
∣
∣
v
∣
∣
2
=
v
1
2
+
v
2
2
+
v
3
2
+
.
.
.
||v||^2=v_1^2+v_2^2+v_3^2+...
∣∣v∣∣2=v12+v22+v32+...
必须收敛于有限和。这类限制条件的无限维向量空间称为希尔伯特空间。
希尔伯特空间的垂直的定义仍然是内积和为0:
w
T
v
=
w
1
v
1
+
w
2
v
2
+
w
3
v
3
+
.
.
.
.
=
0
w^Tv=w_1v_1+w_2v_2+w_3v_3+....=0
wTv=w1v1+w2v2+w3v3+....=0
函数空间
将一个函数视作无限维的向量,这个特殊向量的分量就是函数沿着整个定义域区间的值。如:
f
(
x
)
=
s
i
n
x
,
0
⩽
x
≤
2
π
f(x)=sinx,0\leqslant x \leq 2\pi
f(x)=sinx,0⩽x≤2π
类比一般向量长度的平方,可以视为向量的“面积”,那么函数向量的面积自然是积分。于是函数长度有:
∣
∣
f
∣
∣
2
=
∫
0
2
π
(
s
i
n
x
)
2
d
x
=
∫
0
2
π
1
−
c
o
s
2
x
2
d
x
=
π
||f||^2= \int_{0}^{2\pi}(sinx)^2dx= \int_{0}^{2\pi}\frac{1-cos2x}{2}dx=\pi
∣∣f∣∣2=∫02π(sinx)2dx=∫02π21−cos2xdx=π
那么对于函数
f
,
g
f,g
f,g,函数内积为:
f
T
g
=
∫
a
b
f
(
x
)
⋅
g
(
x
)
d
x
f^Tg=\int_{a}^{b}f(x)\cdot g(x)dx
fTg=∫abf(x)⋅g(x)dx
如果内积为0,则称
f
,
g
f,g
f,g正交。
傅立叶级数
傅立叶级数是一个关于cos和sin的展开式:
y
(
x
)
=
a
0
+
a
1
c
o
s
x
+
b
1
s
i
n
x
+
a
2
c
o
s
2
x
+
b
2
s
i
n
2
x
+
.
.
.
y(x)=a_0+a_1cosx+b_1sinx+a_2cos2x+b_2sin2x+...
y(x)=a0+a1cosx+b1sinx+a2cos2x+b2sin2x+...
项数的规律就是常数
a
0
a_0
a0,余弦项
b
n
c
o
s
n
x
b_ncosnx
bncosnx,正弦项
a
n
s
i
n
n
x
a_nsinnx
ansinnx.
以傅立叶的聪明才智,选取的分量之间应当是正交的。
∫
0
2
π
s
i
n
(
m
x
)
c
o
s
(
n
x
)
d
x
=
1
2
∫
0
2
π
s
i
n
(
m
x
+
n
x
)
+
s
i
n
(
m
x
−
n
x
)
d
x
=
0
\int_{0}^{2\pi}sin(mx)cos(nx)dx= \frac{1}{2}\int_{0}^{2\pi}sin(mx+nx)+sin(mx-nx)dx=0
∫02πsin(mx)cos(nx)dx=21∫02πsin(mx+nx)+sin(mx−nx)dx=0
所以分量正交。
那么
y
(
x
)
y(x)
y(x)与
v
n
=
c
o
s
(
n
x
)
v_n=cos(nx)
vn=cos(nx)的内积为:
y
T
v
n
=
(
a
0
+
b
1
v
1
+
a
1
w
1
+
b
2
v
2
+
a
2
w
2
+
.
.
.
)
T
v
n
=
a
0
v
n
+
b
n
v
n
T
v
n
=
a
0
∫
0
2
π
c
o
s
(
n
x
)
d
x
+
b
n
∫
0
2
π
c
o
s
(
n
x
)
c
o
s
(
n
x
)
d
x
=
0
+
b
n
π
y^Tv_n=(a_0+b_1v_1+a_1w_1+b_2v_2+a_2w_2+...)^Tv_n=a_0v_n+b_nv_n^Tv_n=a_0\int_{0}^{2\pi}cos(nx)dx+b_n\int_{0}^{2\pi}cos(nx)cos(nx)dx=0+b_n\pi
yTvn=(a0+b1v1+a1w1+b2v2+a2w2+...)Tvn=a0vn+bnvnTvn=a0∫02πcos(nx)dx+bn∫02πcos(nx)cos(nx)dx=0+bnπ
所以某一分量
f
f
f的系数为:
b
=
y
T
f
f
T
f
b=\frac{y^Tf}{f^Tf}
b=fTfyTf
例如,
y
(
x
)
y(x)
y(x)在分量
s
i
n
x
sinx
sinx上的投影为:
b
1
s
i
n
x
b1sinx
b1sinx
傅立叶级数恰给出向量y关于一组无限多个相互垂直的坐标轴的坐标。
其他函数空间
在
−
1
⩽
x
≤
1
-1\leqslant x \leq 1
−1⩽x≤1上的多项式函数
f
(
x
)
=
a
0
+
a
1
x
+
a
2
x
2
f(x)=a_0+a_1x+a_2x^2
f(x)=a0+a1x+a2x2,
分量
a
0
a_0
a0,
x
2
x^2
x2的不是正交的。此时可以对
1
,
x
,
x
2
1,x,x^2
1,x,x2进行施密特正交化。
设
v
1
=
1
,
v
2
=
x
v_1=1,v_2=x
v1=1,v2=x,此时求积分有有
v
1
T
v
2
=
0
v_1^Tv_2=0
v1Tv2=0
再设
v
3
=
x
2
+
c
2
v
2
+
c
1
v
1
=
x
2
+
c
2
x
+
c
1
v_3=x^2+c_2v_2+c_1v_1=x^2+c_2x+c_1
v3=x2+c2v2+c1v1=x2+c2x+c1
v
3
T
v
1
=
∫
−
1
1
(
x
2
+
c
2
x
+
c
1
)
d
x
=
2
3
+
2
c
1
=
0
v_3^Tv_1=\int_{-1}^{1}(x^2+c_2x+c_1)dx=\frac{2}{3}+2c_1=0
v3Tv1=∫−11(x2+c2x+c1)dx=32+2c1=0
v
3
T
v
2
=
∫
−
1
1
(
x
3
+
c
2
x
2
+
c
1
x
)
d
x
=
2
3
c
2
=
0
v_3^Tv_2=\int_{-1}^{1}(x^3+c_2x^2+c_1x)dx=\frac{2}{3}c_2=0
v3Tv2=∫−11(x3+c2x2+c1x)dx=32c2=0
所以
v
3
=
x
2
−
1
3
v_3=x^2-\frac{1}{3}
v3=x2−31
用这种方式构造出的多项式称为Legendre(勒让德)多项式,它们在
−
1
⩽
x
≤
1
-1\leqslant x \leq 1
−1⩽x≤1正交。
函数拟合
举例:
0
⩽
x
≤
1
0\leqslant x \leq 1
0⩽x≤1上有
f
(
x
)
=
x
1
2
f(x)=x^\frac{1}{2}
f(x)=x21,用直线
y
=
C
+
D
x
y=C+Dx
y=C+Dx拟合
f
(
x
)
f(x)
f(x).
A
t
=
b
=
[
1
x
]
[
C
D
]
=
[
x
]
At=b=\begin{bmatrix}1 & x \end{bmatrix}\begin{bmatrix} C\\D \end{bmatrix}=\begin{bmatrix} \sqrt{x} \end{bmatrix}
At=b=[1x][CD]=[x]
A
T
(
A
t
−
b
)
=
0
A^T(At-b)=0
AT(At−b)=0
t
=
(
A
T
A
)
−
1
A
T
b
t=(A^TA)^{-1}A^Tb
t=(ATA)−1ATb
注意计算方法不同于一般的矩阵:
矩阵运算法则不变,元素的点乘要化为积分形式。
A
T
A
=
[
1
T
1
1
T
x
x
T
1
x
T
x
]
=
[
1
1
2
1
2
1
3
]
A^TA=\begin{bmatrix} 1^T1 &1^Tx \\ x^T1&x^Tx \end{bmatrix}=\begin{bmatrix} 1 & \frac{1}{2} \\ \frac{1}{2}&\frac{1}{3} \end{bmatrix}
ATA=[1T1xT11TxxTx]=[1212131]
t
=
[
4
15
4
5
]
t=\begin{bmatrix} \frac{4}{15}\\\frac{4}{5} \end{bmatrix}
t=[15454]
函数图像如下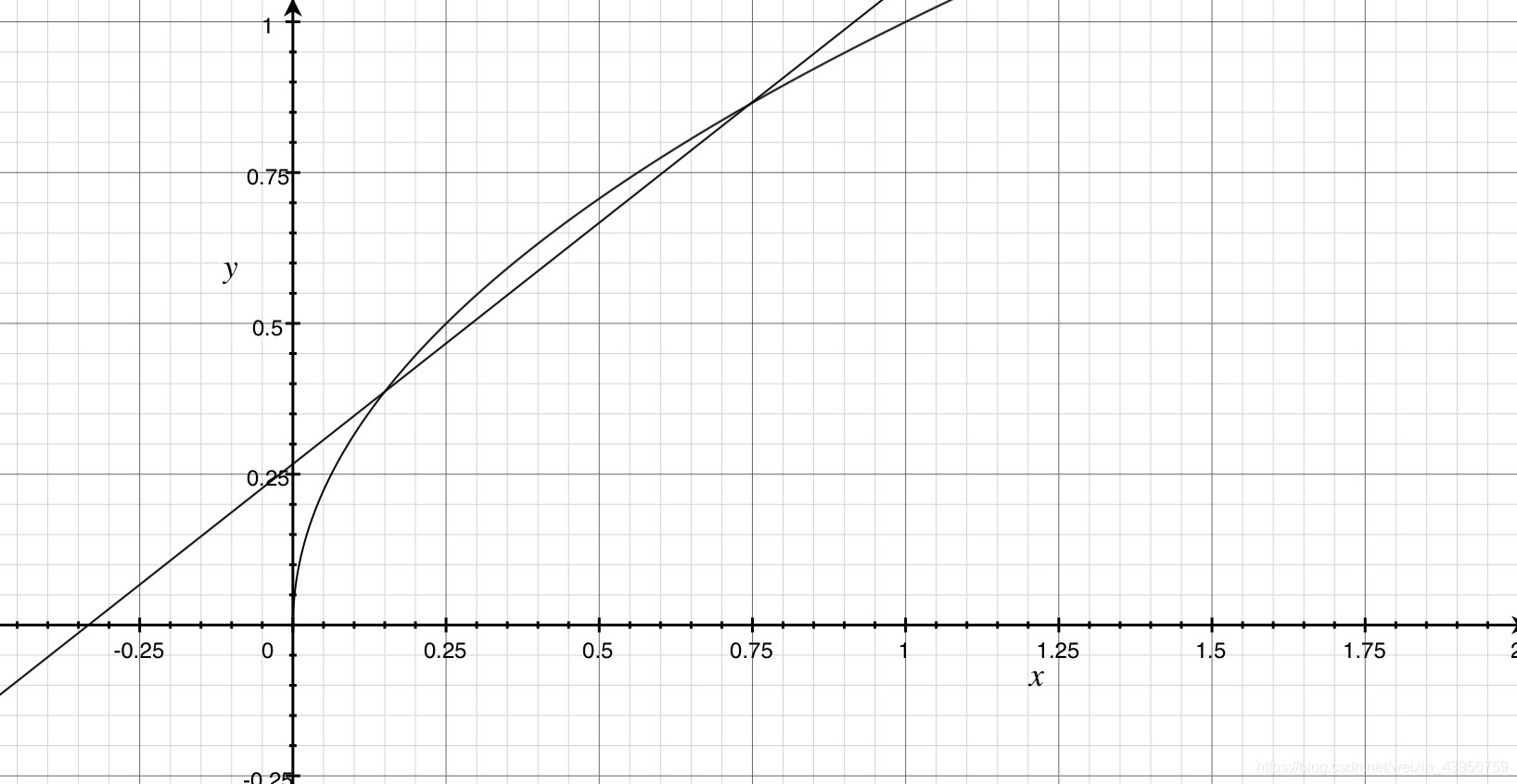





 本文探讨了函数空间的概念,将其与无限维向量空间相联系,并通过傅立叶级数深入理解函数的正交性及投影。同时介绍了希尔伯特空间和勒让德多项式的应用。
本文探讨了函数空间的概念,将其与无限维向量空间相联系,并通过傅立叶级数深入理解函数的正交性及投影。同时介绍了希尔伯特空间和勒让德多项式的应用。
















 735
735

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








