栈模拟二叉树的前序遍历，中序遍历，后序遍历

一、准备工作

首先需要创建一个二叉树，这里我们创建一个简单的二叉树

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;

    TreeNode(int v) : val(v), left(nullptr), right(nullptr) {};
};

int main() {
    TreeNode* root = new TreeNode(1);
    root->left = new TreeNode(2);
    root->right = new TreeNode(3);
    root->left->left = new TreeNode(4);
    root->left->right = new TreeNode(5);
    return 0;
}

这颗二叉树长这样

二、递归解法

当执行二叉树的前序遍历时，首先访问根节点，然后按照"根-左-右"的顺序依次访问所有节点。具体步骤如下：

1. 访问根节点。
2. 递归地对根节点的左子树进行前序遍历。
3. 递归地对根节点的右子树进行前序遍历。

当执行二叉树的中序遍历时，首先访问左子树，然后按照"左-根-右"的顺序依次访问所有节点。具体步骤如下：

1. 递归地对根节点的左子树进行中序遍历。
2. 访问根节点。
3. 递归地对根节点的右子树进行中序遍历。

当执行二叉树的后序遍历时，首先访问左子树，然后按照"左-右-根"的顺序依次访问所有节点。具体步骤如下：

1. 递归地对根节点的左子树进行后序遍历。
2. 递归地对根节点的右子树进行后序遍历。
3. 访问根节点。

所以递归的解法就非常简单

2.1、前序遍历

void dfs(TreeNode* root) {
    if (root == nullptr) return;

    cout << root->val << endl;
    dfs(root->left);
    dfs(root->right);
}

2.2、中序遍历

void dfs(TreeNode* root) {
    if (root == nullptr) return;

    dfs(root->left);
    cout << root->val << endl;
    dfs(root->right);
}

2.3、后序遍历

void dfs(TreeNode* root) {
    if (root == nullptr) return;

    dfs(root->left);
    dfs(root->right);
    cout << root->val << endl;
}

三、栈解法

栈解法本质上是在模拟递归，因为在递归的过程中使用了系统栈，所以在迭代的解法中常用 Stack 来模拟系统栈。为什么会有栈解法，因为栈解法在一些特殊场合会很适用，例如找到二叉搜索树的第k个值，在找到后直接推出就可以了，不用像递归一样要全部遍历一遍。

3.1、前序遍历

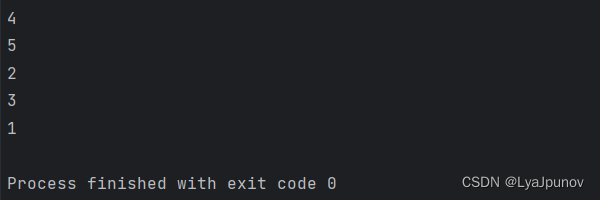
首先我们应该创建一个栈用来存放节点，我们想要打印根节点的数据，此时栈里面的内容为空，所以我们优先将头结点加入栈，然后打印。之后我们应该先打印左子树，然后右子树。所以先加入栈的就是右子树，然后左子树。这里利用了栈的先进后出的特性

void dfs(TreeNode* root) {
    stack<TreeNode*> st;
    st.push(root);

    while (!st.empty()) {
        TreeNode *t = st.top();
        st.pop();

        cout << t->val << endl;
        if (t->right) st.push(t->right);
        if (t->left) st.push(t->left);
    }
}

3.2、中序遍历

1. 创建一个栈，然后按 左 中 右的顺序输出节点。
2. 尽可能的将这个节点的左子树压入栈，此时栈顶的元素是最左侧的元素，其目的是找到一个最小单位的子树(也就是最左侧的一个节点)，并且在寻找的过程中记录了来源，才能返回上层,同时在返回上层的时候已经处理完毕左子树了
3. 当处理完最小单位的子树时，返回到上层处理了中间节点。（如果把整个左中右的遍历都理解成子树的话，就是处理完 左子树->中间(就是一个节点)->右子树）
4. 如果有右节点，其也要进行中序遍历。

void dfs(TreeNode* root) {
    stack<TreeNode*> st;

    TreeNode* t = root;
    while (!st.empty() || t != nullptr) {
        while (t) {
            st.push(t);
            t = t->left;
        }

        TreeNode* t2 = st.top();
        st.pop();
        cout << t2->val << endl;

        if (t2->right) t = t2->right;
    }
}

3.3、后序遍历

1. 前序遍历的过程是 中–左–右。
2. 将其转化成 中–右–左。也就是压栈的过程中优先压入左子树，在压入右子树。
3. 然后将这个结果返回来，这里是利用栈的先进后出倒序打印。

void dfs(TreeNode* root) {
    stack<TreeNode*> st1;
    stack<TreeNode*> st2;
    st1.push(root);

    while (!st1.empty()) {
        TreeNode* node = st1.top();
        st1.pop();
        st2.push(node);
        if (node->left != nullptr) {
            st1.push(node->left);
        }
        if (node->right != nullptr) {
            st1.push(node->right);
        }
    }

    while (!st2.empty()) {
        cout << st2.top()->val << endl;
        st2.pop();
    }
}

四、Morris解法

morris解法还没学会。。。而且也没咋看到别人用，这里暂时放弃