数据分析-深度学习 Day1

目录：

第一节 机器学习&深度学习介绍

第二节 机器学习攻略

一、机器学习的框架

二、模型训练攻略

三、针对Optimization Issue的优化，类神经网络训练不起来怎么办

(一) 局部最优点和鞍点

(二) 批处理和momentum

(三) 自动调节学习率Learning rate

(四) 损失函数带来的影响

第二节 模型训练攻略

一、机器学习的框架

二、模型训练攻略

三、针对Optimization Issue的优化，类神经网络训练不起来怎么办

(一) 局部最优点和鞍点

(二) 批处理和momentum

(三) 自动调节学习率Learning rate

(四) 损失函数带来的影响

本节主要介绍下机器学习和深度学习

1、机器学习的本质

机器学习主要的本质是寻找一个这样一个Function函数，并且使得这个函数具有某种能力，比如声音识别、图像分类、Playing Go等能力。

2、机器学习三大任务

针对不同的函数，自然对应不同的任务，通常我们可以简单的将机器学习任务分为两大类，一类是Regression（回归），一类是Classification（分类），但是在机器学习里面，我们还有一类任务是Structured Learning（结构化学习），意思就是说，当前的机器学习任务已经不仅仅局限于产生一个数字，或者做个简单的分类，而是希望机器能够生成一个有结构的物件，比如画一张图，写一篇文章等等，这种能力可以被称为让机器学会“创造”。

3、如何找到Function函数

假设我们现在有一个任务是做图像分类， 此时我们就需要找到一个函数，并且希望这个函数能够完成当前的任务，通常来讲，要找到这样一个函数需要通过以下三步曲：

定义一个Function with unknown parameters（比如 y=wTx+b ）

定义一个Loss from training data（比如 L=1N∑i=1N(y−y^)2 ）

Optimzation Loss Function（比如SGD）

4、双层神经网络

1. Function 函数

双层神经网络就是在假设空间中寻找一个相对比较复杂的模型。对于比较简单的任务或者场景，也许只需要定义一个线性模型就能解决问题，但是通常情况下，面对复杂的环境条件和任务下，简单的线性模型往往拟合程度不够，存在模型偏差。因此，在这种情况下，想要在假设空间中找一个Function函数，往往需要对应的较为复杂的模型，我们知道，神经网络有一个万能逼近定理，即它可以拟合和逼近任意函数（万能逼近定理可以参考以下两篇知乎文章）

Taylor Wu：寻根问底：为什么神经网络可以作为通用函数逼近器?53 赞同 · 9 评论文章

神经网络的万能逼近定理已经发展到什么地步了？2182 关注 · 27 回答问题

而神经网络本质上是一堆激活函数的线性组合（这里我们特指双层神经网络），因此我们可以得到这样一个通式：

y=b+∑iciσ(bi+∑jwijxj)

其中 σ 就是激活8函数， b+∑jwijxj 表示是数据是输入是多维向量，或者说是多维特征的，单个数据有 j 维，用图展示就是如下所示：

写成矩阵的形式就是： y=b+cTσ(b+wx) ，这就是两层的神经网络（输入层、中间层、输出层）

看到这里有人也许会觉得双层的神经网络是不是就足够可以拟合出我们想要的函数了呢？答案是：理论证明，两层神经网络可以无限逼近任意连续函数。

需要注意的是，相对于单层神经网络，也就是单层感知机，是没有办法处理非线性问题的，而双层神经网络的，通过引入激活函数，可以处理非线性问题，那两层神经网络为什么就可以做非线性任务呢？本质就是，从输入层到隐藏层时，数据发生了空间变换。也就是说，两层神经网络中，隐藏层对原始的数据进行了一个空间变换，使其可以被线性分类，然后输出层的决策分界划出了一个线性分类分界线，对其进行分类。感兴趣的同学可以参考下面这篇博文：

神经网络浅讲：从神经元到深度学习 - 计算机的潜意识 - 博客园www.cnblogs.com/subconscious/p/5058741.html

同时，我们知道，对于高维空间的数据，更容易使数据变得线性可分，这也是为什么神经网络往往在输出层节点数这么多的原因。

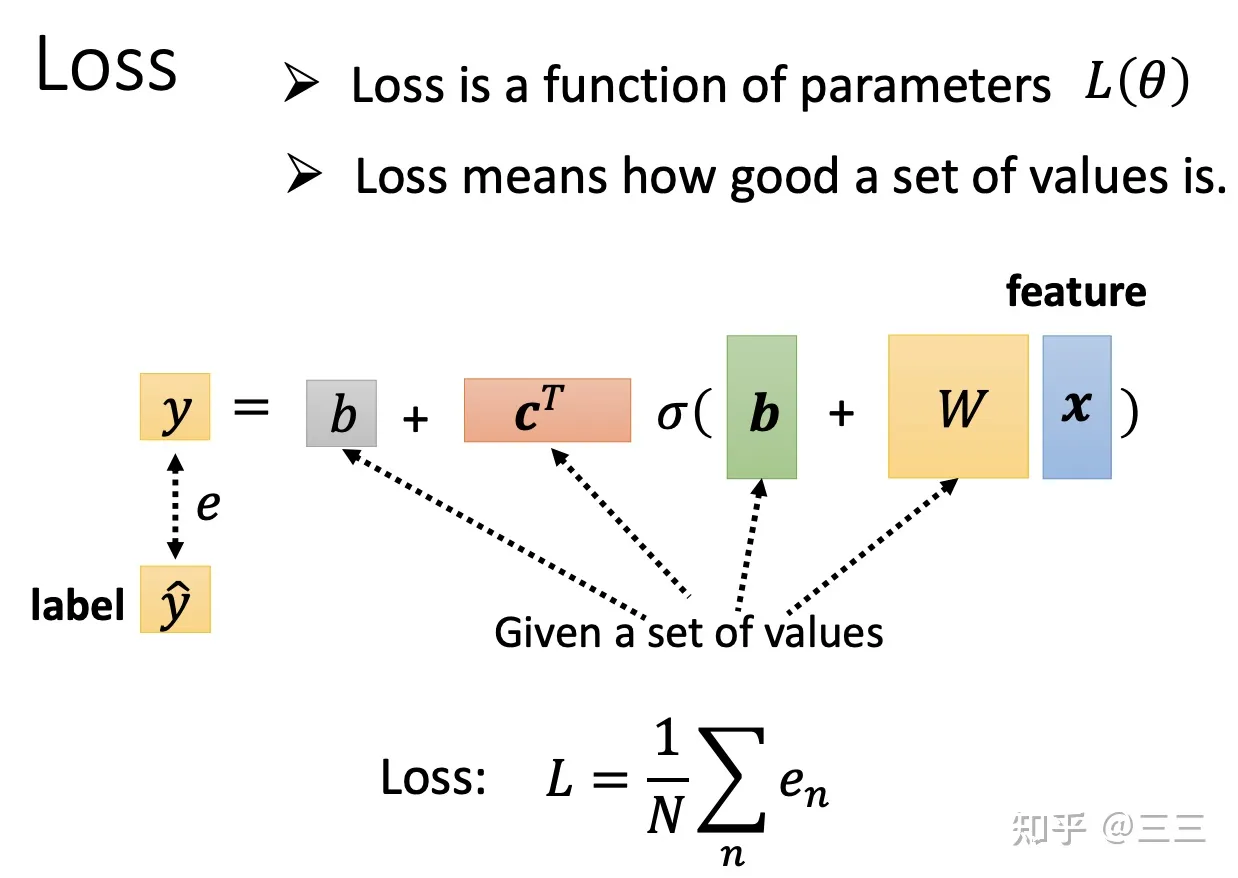
2. Loss 损失

Loss损失的定义可以根据具体的任务做相应的设定，本质是定义一个预测label和实际label之间的一个距离关系。