【点云系列】 A Rotation-Invariant Framework for Deep Point Cloud Analysis

1. 概要

TVCG 2021期刊
代码：https://github.com/nini-lxz/Rotation-Invariant-Point-Cloud-Analysis

2. 动机

现阶段方法的共同问题就是：旋转不变性没有被保证
所以所提出的方法就是保证了这一点。

使用一个低层语义的 旋转不变性的表达 来替代 3D笛卡尔坐标输入，有点类似使用手工设计的具有旋转不变性的特征拿给网络学最优的过程。

3. 方法

3.1 常用方法特征提取$A$

基于全局特征$G_i$+局部特征$L_{ij}$ + 非线性函数$h_{\theta }$
其中$A$是对称函数。

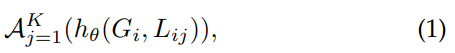
3.2 旋转不变性

一个框架具有旋转不变性 = 网络输入具有旋转不变性（其实是对输入点云提取了具有旋转不变性的表达来代替原始点云作为输入） + 操作子具有旋转不变性

网络输入设计

考虑一下4点：

1. 亦即无论输入点云$S$如何变换，提取到的具有旋转不变性的表达是保持不变的。设提取旋转不变性的函数为$\Phi$，那么需要满足：
   
   这里的R指的是在3D坐标当中进行任意旋转。
2. 满足公式（2）中简单使用L2距离或相对角度作为输入太过于粗糙，且信息有所丢失；
3. 不会产生歧义性，也即不同局部区域都有各自的旋转不变性表达；
4. 需要抗噪；

网络架构设计

考虑一下两点：

1. 网络框架不能包含任何的旋转变性的操作，例如不可以指定顺序
2. 网络框架不包括点云坐标，而只是相关几何信息，例如距离角度等作为输入；

3.3 卷转不变性表达

1. 预处理：
   首先对输入点云$S$进行归一化，在单元球体。
   然后使用PointNet++li d query ball 来定义临近点 { p i j } j = 1 K \{ p_{ij}\}^K_{j=1} { pij​}j=1K​，如下图2(a)与(b)。

2. 计算：
   提取特征$G_i$与$p_i$的局部特征 { L i j } j = 1 K \{L_{ij}\}^K_{j=1} { Li