差分数组+例题：Pikachu

最新推荐文章于 2025-05-23 12:00:00 发布

THE END GAME

最新推荐文章于 2025-05-23 12:00:00 发布

阅读量737

点赞数 1

CC 4.0 BY-SA版权

分类专栏：差分数组

本文链接：https://blog.youkuaiyun.com/weixin_43870114/article/details/90676843

本文介绍了差分数组的概念、性质及其在区间加减操作和区间和查询问题中的应用。通过差分数组，可以高效地处理离线数列的问题，避免了对每个元素的逐一遍历，提升了算法效率。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

…比赛遇到，我都不知道这是个啥…(太菜了太菜了)
一、差分数组的定义及用途
1.定义：
对于已知有n个元素的离线数列d，我们可以建立记录它每项与前一项差值的差分数组f：显然，f[1]=d[1]-0=d[1];对于整数i∈[2,n]，我们让f[i]=d[i]-d[i-1]。
2.简单性质：
(1)计算数列各项的值：观察d[2]=f[1]+f[2]=d[1]+d[2]-d[1]=d[2]可知，数列第i项的值是可以用差分数组的前i项的和计算的，即d[i]=f[i]的前缀和。
(2)计算数列每一项的前缀和：第i项的前缀和即为数列前i项的和，那么推导可知
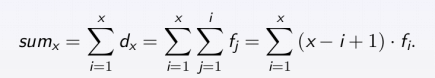
在这里插入图片描述
即可用差分数组求出数列前缀和；
3.用途：
(1)快速处理区间加减操作：
假如现在对数列中区间[L,R]上的数加上x，我们通过性质(1)知道，第一个受影响的差分数组中的元素为f[L],即令f[L]+=x，那么后面数列元素在计算过程中都会加上x；最后一个受影响的差分数组中的元素为f[R],所以令f[R+1]-=x，即可保证不会影响到R以后数列元素的计算。这样我们不必对区间内每一个数进行处理，只需处理两个差分后的数即可；
(2)询问区间和问题：
由性质(2)我们可以计算出数列各项的前缀和数组sum各项的值；那么显然，区间[L,R]的和即为ans=sum[R]-sum[L-1];

例题：
在这里插入图片描述

维护两个差分数组，逆序遍历，因为改变的都是之前的操作数

#include<algorithm>
#include<cstdio>
#include<cmath>
#include<iostream>
#include<cstring>
#include<set>
#include<map>
#include<iterator>
#include<queue>
#include<vector>
#include<string>
using namespace std;

typedef long long ll;
const int N=1e6+10;
const long long INF=1e18;
const double eps