SMAA算法详解 - AreaTex

AreaTex

• 以下均在无SubPixel的情况下，即offset = (0,0)。subpixel将单独讲解。

areaortho.area

# Calculates the area under the line p1->p2, for the pixel x..x+1:
    def area(p1, p2, x):

---

1. 计算底边长

	d = p2[0] - p1[0], p2[1] - p1[1]
        x1 = float(x)
        x2 = x + 1.0
        y1 = p1[1] + d[1] * (x1 - p1[0]) / d[0]
        y2 = p1[1] + d[1] * (x2 - p1[0]) / d[0]

依据三角形相似原理：
Y1 / (x1 - p1[0]) = d[1] / d[0] => Y1 = d[1] * (x1 - p1[0]) / d[0]
p1 = [0, o2] = [0, 0.5 + offset - 1.0] => p1[1] < 0
所以：y1 = p1[1] + Y1 = p1[1] + d[1] * (x1 - p1[0]) / d[0]
同理：y2 = p1[1] + Y2 = p1[1] + d[1] * (x2 - p1[0]) / d[0]

---

2. 判断是梯形还是三角形

inside = (x1 >= p1[0] and x1 < p2[0]) or (x2 > p1[0] and x2 <= p2[0])
        if inside:
            istrapezoid = (copysign(1.0, y1) == copysign(1.0, y2) or 
                           abs(y1) < 1e-4 or abs(y2) < 1e-4)

---

3. 计算面积
   一个梯形：
   
   area = (y1 + y2) * (x2 - x1) / 2
   其中：x2 - x1 = 1
   area = abs(y1 + y2) / 2
   a1 = area
   a2 = 0

两个三角形：

a1 = (x - x1) * y1 / 2
设 X1 = x - x1，要求面积，就要求出 X1。
从图中可以看出，X1 正好是 X 的小数部分。
只要求出X就能得出面积。
根据三角形相似，
X = (-1 * p1[1]) * d[0] / d[1]
x = X + p1[0] = -p1[1] * d[1] / d[1] + p1[0]
所以，a1 = y1 * modf(x) / 2
同理：a2 = y2 * (1 - modf(x)) / 2

---

areaortho

# Horizontal/Vertical Areas

# Calculates the area for a given pattern and distances to the left and to the
# right, biased by an offset:
def areaortho(pattern, left, right, offset):

计算横向 / 纵向锯齿类型的面积。
patterns

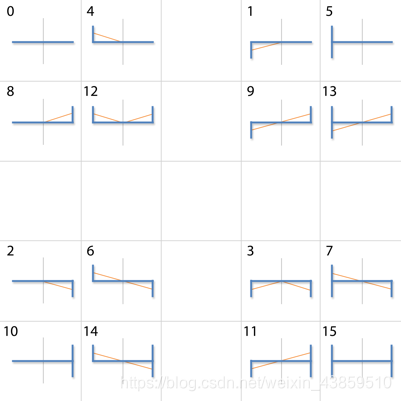
具体计算略，套公式即可

---

smootharea

# Smoothing function for small u-patterns:
def smootharea(d, a1, a2):
    b1 = (a1 * 2.0).sqrt() * 0.5
    b2 = (a2 * 2.0).sqrt() * 0.5
    p = saturate(d / float(SMOOTH_MAX_DISTANCE))
    return lerp(b1, a1, p), lerp(b2, a2, p)

短U型锯齿有重复部分。
中间两个三角形面积为a1, a2。
计算时，左边a1只计算像素左边部分, 右边a2只计算像素右边部分。
为了得到整个像素的值，融合a1, a2，得到一个平滑过渡值。
长U型锯齿不存在交集。
计算时a1, a2必定有一个为 0. 即使参与计算也不会改变值。

tex2dortho

# Creates a 2D orthogonal pattern subtexture:
def tex2dortho(args):
    pattern, path, offset = args
    size = (SIZE_ORTHO - 1)**2 + 1
    tex2d = Image.new("RGBA", (size, size))
    for y in range(size):
        for x in range(size):
            p = areaortho(pattern, x, y, offset)
            p = p[0], p[1], 0.0, 1.0
            tex2d.putpixel((x, y), bytes(p))

计算直角锯齿面积
SIZE_ORTHO = 16
16个像素能存放[0 - 15]，也就是搜索的最大距离只有15。
对于纹理边界是不够用的。
为了能访问到更大的距离，size = (SIZE_ORTHO - 1)^2 + 1 = 226。

pattern7(226 * 226)

---

tex4dortho

把tex2dortho计算后的tex2d存入tex4d的左半部分。

# Calculate the orthogonal patterns 4D texture for a given offset:
def tex4dortho(tex4d, files, y, offset):

tex2dortho得出的tex2d
size = 226 * 226，但是每个pattern在tex4d中占的大小是 16 * 16，
这样就需要一个压缩算法，用16个像素存放226个值。
观察上面pattern 7纹理图，基本还是一个线性变化的值。
所以以坐标：x = x ^ 2, y = y ^ 2，取16个值。
通过tex4d双线性采样，得出误差很小的值。
距离越小，精度越大，很长的锯齿可以忽略误差。

---

areadiag.area1

# Calculates the area under the line p1->p2 for the pixel 'p' using brute
    # force sampling:
    # (quick and dirty solution, but it works)
    def area1(p1, p2, p):

在这里使用了暴力计算。
将一个像素分成 SAMPLES_DIAG * SAMPLES_DIAG = 30 * 30 = 900个小区块。
把在p1->p2这条射线的下方的小区块相加，除以900。
其实就是计算该像素点在p1->p2下方的面积。

为什么要暴力计算呢？
直接计算面积的话，就要分清各种锯齿形状，麻烦！
这种方式，只需要判断小区块是否在线的下方，相加即可。

但是，这种方式会产生2个问题：

第一：判断小区块是否在p1->p2下面时，与p1->p2相邻的小区块的计算会存在误差，导致错误。
临近的点最多也只有30个，不会对结果有实质性改变。

第二：如下图，分成了30 * 30 = 900个小块.
白色线条为p1->p。
p1->p2下方的小块数量是 ：(900 - 30) / 2 = 435，面积是：435 / 900 = 0.4833333
p1->p2上方以及p1->p2上的数量是 (900 - 435) = 465，面积是：0.51666667
所以，计算后的权重会存在小范围误差。

areadiag.area

# Calculates the area under the line p1->p2:
    # (includes the pixel and its opposite)
    def area(p1, p2, left, offset):
        e1, e2 = edgesdiag[pattern]
        p1 = p1 + vec2(*offset) if e1 > 0 else p1
        p2 = p2 + vec2(*offset) if e2 > 0 else p2
        a1 = area1(p1, p2, vec2(1.0, 0.0) + vec2(left, left))
        a2 = area1(p1, p2, vec2(1.0, 1.0) + vec2(left, left))
        return vec2(1.0 - a1, a2)

图示：灰黑色部分表示所求部分

---

areadiag

计算对角线面积

# Diagonal Areas

# Calculates the area for a given pattern and distances to the left and to the
# right, biased by an offset:
def areadiag(pattern, left, right, offset):

pattern 类型.

大致计算目标图示：

具体计算略，套公式即可

---

tex2ddiag

# Creates a 2D diagonal pattern subtexture:
def tex2ddiag(args):
    pattern, path, offset = args
    tex2d = Image.new("RGBA", (SIZE_DIAG, SIZE_DIAG))
    for y in range(SIZE_DIAG):
        for x in range(SIZE_DIAG):
            p = areadiag(pattern, x, y, offset)
            p = p[0], p[1], 0.0, 0.0
            tex2d.putpixel((x, y), bytes(p))
    tex2d.save(path, "TGA")

对角线tex2d

---

tex4ddiag

把tex2ddiag装入tex4d的右半部分。

# Calculate the diagonal patterns 4D texture for a given offset:
def tex4ddiag(tex4d, files, y, offset):

---

assemble

# Assembles 2D pattern subtextures into a 4D texture:
def assemble(tex4d, files, edges, pos, size, compress):

把tex2d装入tex4d中

---