信号处理:<一> DFT和FFT
DFT,即离散傅里叶变化,是傅里叶变换在时域和频域上都呈离散的形式,将信号的时域采样变换为其DTFT的频域采样。
1、 DFT数学表达式
X
[
k
]
=
∑
n
=
0
N
x
[
n
]
W
N
k
n
=
∑
n
=
0
N
x
[
n
]
e
−
j
2
π
k
n
N
X[k] = \sum\limits_{n = 0}^N {x[n]} W_N^{kn} = \sum\limits_{n = 0}^N {x[n]} {e^{ - j\frac{{2\pi k{\rm{n}}}}{N}}}
X[k]=n=0∑Nx[n]WNkn=n=0∑Nx[n]e−jN2πkn
其中
0
≤
k
≤
N
{0 \le k \le N}
0≤k≤N。
从上式可以看出,做DFT需要
N
2
N^2
N2次复数乘法和
N
(
N
−
1
)
N(N-1)
N(N−1)次复数加法【求一个点X[k]需要
N
N
N次复数乘法和
N
−
1
N-1
N−1次复数加法】,而一次复数乘法又由4次实数乘法和2次实数加法构成,一次复数加法由2次实数加法构成,具体解释如下:
(
a
+
j
b
)
∙
(
c
+
j
d
)
=
[
a
c
−
b
d
]
+
j
[
a
d
+
b
c
]
(
a
+
j
b
)
+
(
c
+
j
d
)
=
[
a
+
c
]
+
j
[
b
+
d
]
\begin{array}{l} \left( {a + jb} \right) \bullet \left( {c + jd} \right) = \left[ {ac - bd} \right] + j\left[ {ad + bc} \right]\\ \left( {a + jb} \right) + \left( {c + jd} \right) = \left[ {a + c} \right] + j[b + d] \end{array}
(a+jb)∙(c+jd)=[ac−bd]+j[ad+bc](a+jb)+(c+jd)=[a+c]+j[b+d]因此,作DFT需要
4
N
2
4N^2
4N2次实数乘法和
(
2
N
2
+
2
N
2
−
2
N
)
或
[
2
(
2
N
2
−
N
]
(2N^2+2N^2-2N)或[2(2N^2-N]
(2N2+2N2−2N)或[2(2N2−N]次实数加法。为了降低复杂度,引出了FFT算法,其思想为用分解的思想将N点DFT的计算依次分解为尺寸较小的DFT计算并利用复数
W
N
k
n
W_N^{kn}
WNkn的周期性和对称性计算。
2 、 W N k n W_N^{kn} WNkn的理解
W
N
k
n
=
e
−
j
2
π
k
n
/
N
=
c
o
s
(
j
2
π
k
n
/
N
)
−
j
s
i
n
(
j
2
π
k
n
/
N
)
W_N^{kn}=e ^{-j2\pi kn/N}=cos(j2 \pi kn/N)-jsin(j2 \pi kn/N)
WNkn=e−j2πkn/N=cos(j2πkn/N)−jsin(j2πkn/N),
W
N
k
n
W_N^{kn}
WNkn是
W
N
W_N
WN的kn次幂,
W
N
1
=
e
−
j
2
π
k
n
/
N
=
c
o
s
(
j
2
π
/
N
)
−
j
s
i
n
(
j
2
π
/
N
)
W_N^{1}=e ^{-j2\pi kn/N}=cos(j2 \pi /N)-jsin(j2 \pi /N)
WN1=e−j2πkn/N=cos(j2π/N)−jsin(j2π/N),
W
N
1
W_N^{1}
WN1可以理解为将单位圆360角化为
N
N
N份,因此$W_N^{1}实际上就是一个在复平面单位圆上旋转的值。如下图所示:将单位圆对应的360划分为8份,则每一份所对应的为45度。
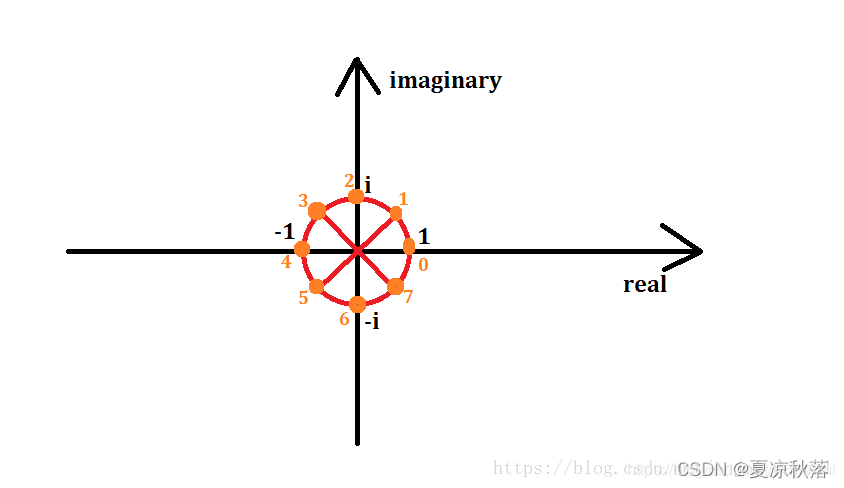
从图中不难得出旋转因子的性质:
a)周期性:
W
N
a
+
N
=
W
N
a
W_N^{a+N}=W_N^{a}
WNa+N=WNa
b) 对称性:
W
N
a
+
N
/
2
=
−
W
N
a
W_N^{a+N/2}=-W_N^{a}
WNa+N/2=−WNa
c) 缩放性:
W
N
2
=
−
W
N
/
2
1
W_N^{2}=-W_{N/2}^{1}
WN2=−WN/21
2 、FFT的理解
2.1 基于时间的傅里叶变化
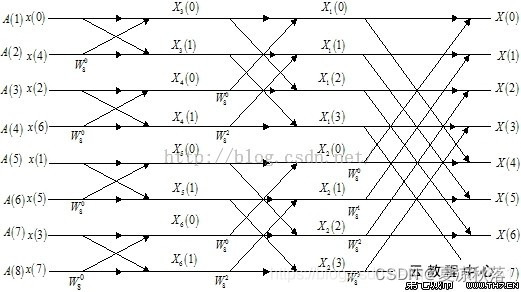
如图所示:
x
(
n
)
x(n)
x(n)分解为偶数与奇数的两个序列之和,即
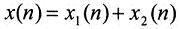
x
1
(
n
)
x1(n)
x1(n)和
x
2
(
n
)
x2(n)
x2(n)的长度都是
N
/
2
N/2
N/2,
x
1
(
n
)
x_1(n)
x1(n)是偶数序列,
x
2
(
n
)
x_2(n)
x2(n)是奇数序列,
x
1
(
n
)
=
x
(
2
n
)
x_1(n)=x(2n)
x1(n)=x(2n),
x
2
(
n
)
=
x
(
2
n
+
1
)
x_2(n)=x(2n+1)
x2(n)=x(2n+1),
n
=
0
,
1...
N
/
2
−
1
n=0,1...N/2-1
n=0,1...N/2−1。则
X
(
k
)
=
∑
n
=
0
(
n
为
偶
数
)
N
x
[
n
]
W
N
k
n
+
∑
n
=
0
(
n
为
奇
数
)
N
x
[
n
]
W
N
k
n
=
∑
n
=
0
N
/
2
−
1
x
1
[
n
]
W
N
2
k
n
+
∑
n
=
0
N
/
2
−
1
x
[
n
]
W
N
k
(
2
n
+
1
)
X(k)= \sum\limits_{n = 0(n为偶数)}^N {x[n]} W_N^{kn}+\sum\limits_{n = 0(n为奇数)}^N {x[n]} W_N^{kn}=\sum\limits_{n = 0}^{N/2-1} {x_1[n]} W_N^{2kn}+\sum\limits_{n = 0}^{N/2-1} {x[n]} W_N^{k(2n+1)}
X(k)=n=0(n为偶数)∑Nx[n]WNkn+n=0(n为奇数)∑Nx[n]WNkn=n=0∑N/2−1x1[n]WN2kn+n=0∑N/2−1x[n]WNk(2n+1)
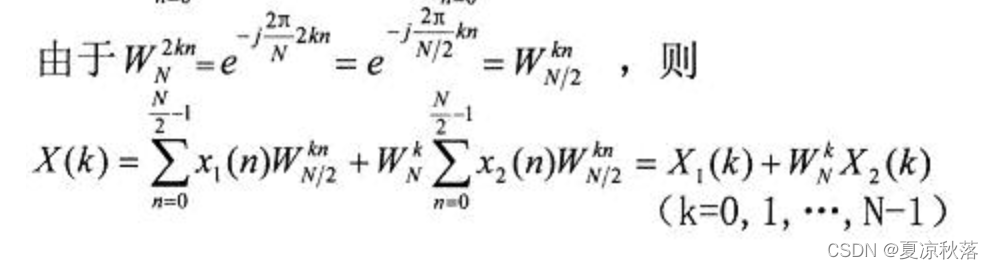 其中
X
1
(
k
)
X_1(k)
X1(k)和
X
2
(
k
)
X_2(k)
X2(k)分别为
x
1
(
n
)
x_1(n)
x1(n)和
x
2
(
n
)
x_2(n)
x2(n)的N/2点DFT。
其中
X
1
(
k
)
X_1(k)
X1(k)和
X
2
(
k
)
X_2(k)
X2(k)分别为
x
1
(
n
)
x_1(n)
x1(n)和
x
2
(
n
)
x_2(n)
x2(n)的N/2点DFT。
X
1
[
k
]
=
∑
n
=
0
N
/
2
−
1
x
1
[
n
]
W
N
/
2
k
n
X_1[k] = \sum\limits_{n = 0}^{N/2-1} {x_1[n]} W_{N/2}^{kn}
X1[k]=n=0∑N/2−1x1[n]WN/2kn
X
2
[
k
]
=
∑
n
=
0
N
/
2
−
1
x
2
[
n
]
W
N
/
2
k
n
X_2[k] = \sum\limits_{n = 0}^{N/2-1} {x_2[n]} W_{N/2}^{kn}
X2[k]=n=0∑N/2−1x2[n]WN/2kn
由于
X
1
(
k
)
X_1(k)
X1(k)和
X
2
(
k
)
X_2(k)
X2(k)均以N/2为周期,且由对称性知
W
N
k
+
N
/
2
=
−
W
N
k
W_N^{k+N/2}=-W_N^{k}
WNk+N/2=−WNk,所以X(k)又可表示为:
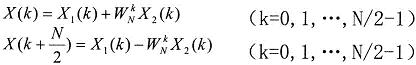
上式的运算可以用下图表示,根据其形状称之为蝶形运算。
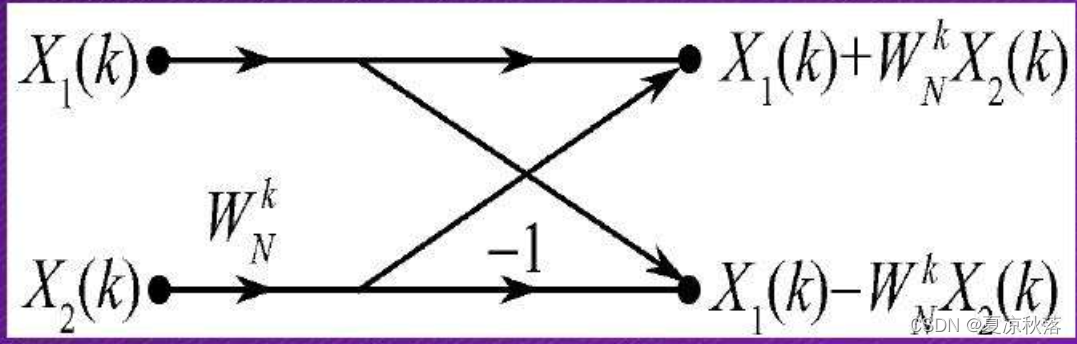
从上图可以看出将N点DFT分解为N/2个两点DFT,计算一个碟形运算需要1次复数乘法和2次复数加法。以最开始给的N=8为例,
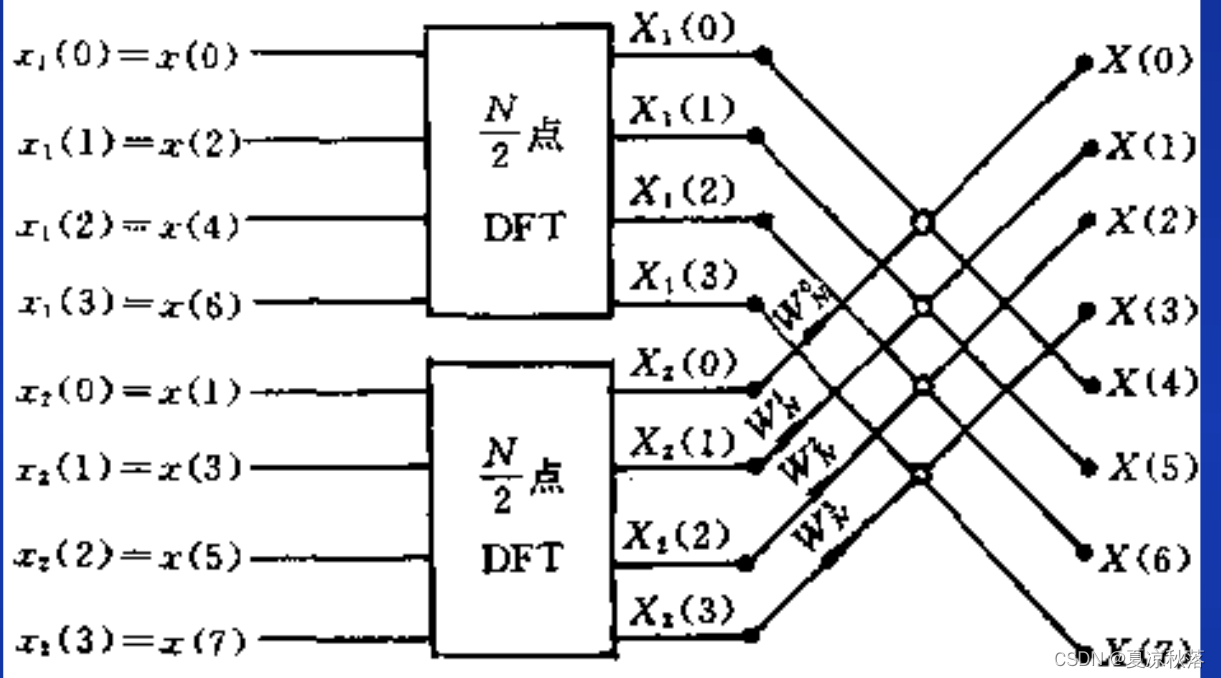 计算一个
N
N
N点的DFT需要计算两个
N
/
2
N/2
N/2的DFT和N/2的蝶形运算,依次类推,可以发现,计算N点的DFT最终可以分成N/2个两个的DFT,通过归纳可以发现,N点的DFT总共可以分为
l
o
g
2
N
log_2^{N}
log2N级,每级有
N
/
2
N/2
N/2个蝶形运算构成,因此每级总共有
N
/
2
次
N/2次
N/2次复乘和
N
N
N次复加,一个
N
N
N点的DFT总共有
N
/
2
l
o
g
2
N
N/2log_2^{N}
N/2log2N次复数乘法和
N
l
o
g
2
N
Nlog_2^{N}
Nlog2N
计算一个
N
N
N点的DFT需要计算两个
N
/
2
N/2
N/2的DFT和N/2的蝶形运算,依次类推,可以发现,计算N点的DFT最终可以分成N/2个两个的DFT,通过归纳可以发现,N点的DFT总共可以分为
l
o
g
2
N
log_2^{N}
log2N级,每级有
N
/
2
N/2
N/2个蝶形运算构成,因此每级总共有
N
/
2
次
N/2次
N/2次复乘和
N
N
N次复加,一个
N
N
N点的DFT总共有
N
/
2
l
o
g
2
N
N/2log_2^{N}
N/2log2N次复数乘法和
N
l
o
g
2
N
Nlog_2^{N}
Nlog2N
直接计算DFT和利用FFT计算DFT的运算量对比如下图所示:

3、编程思想
3.1 原位计算

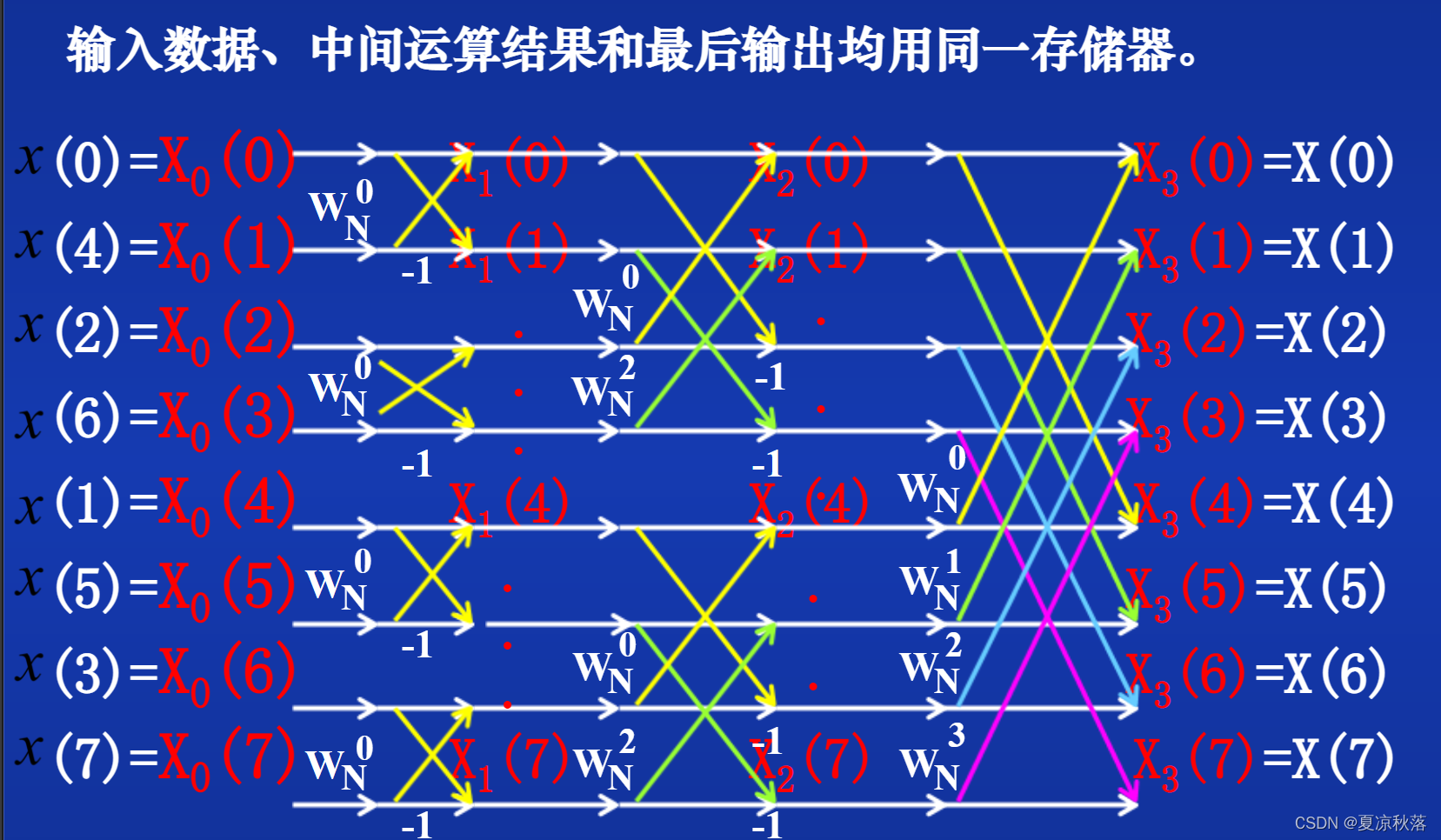


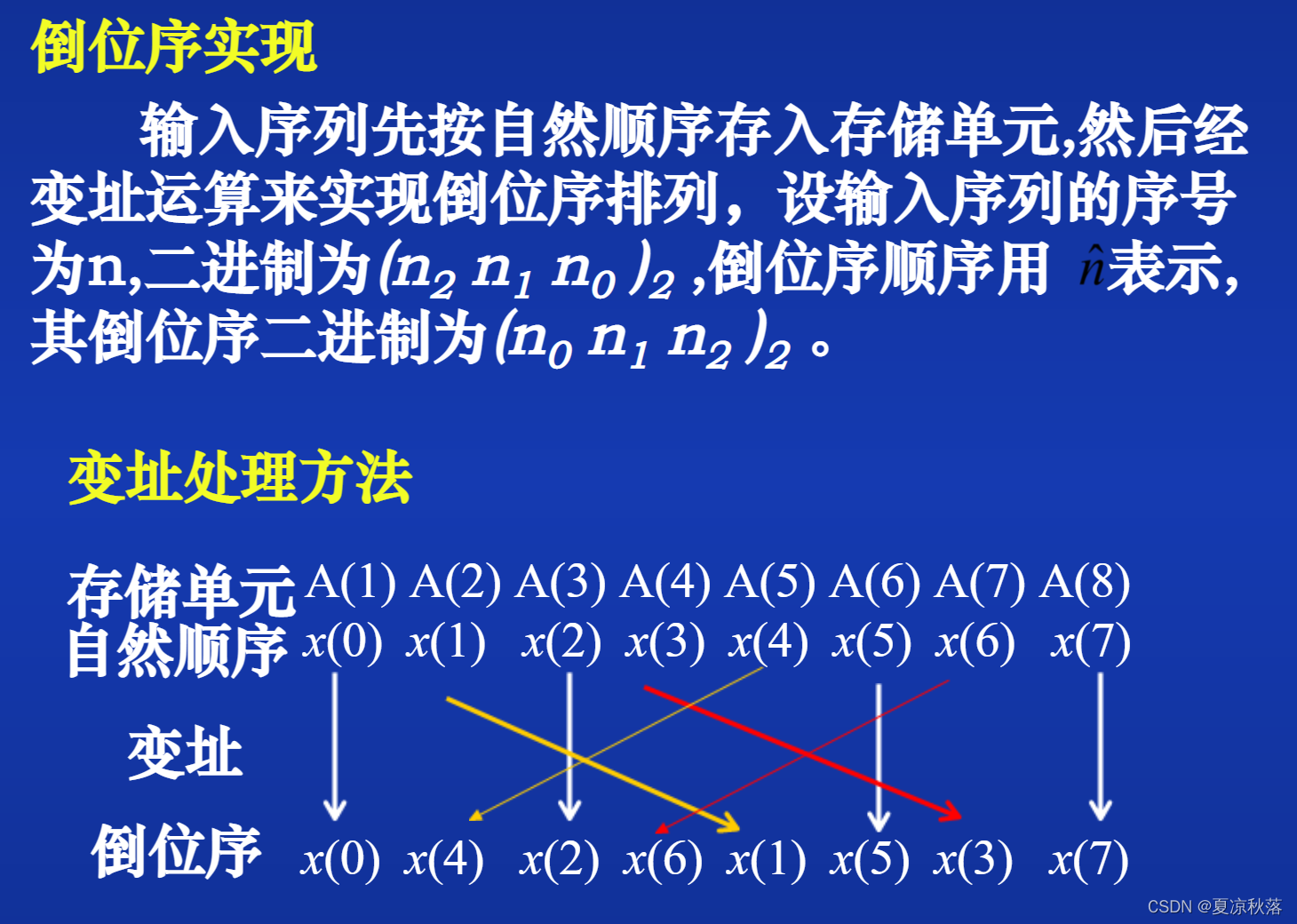
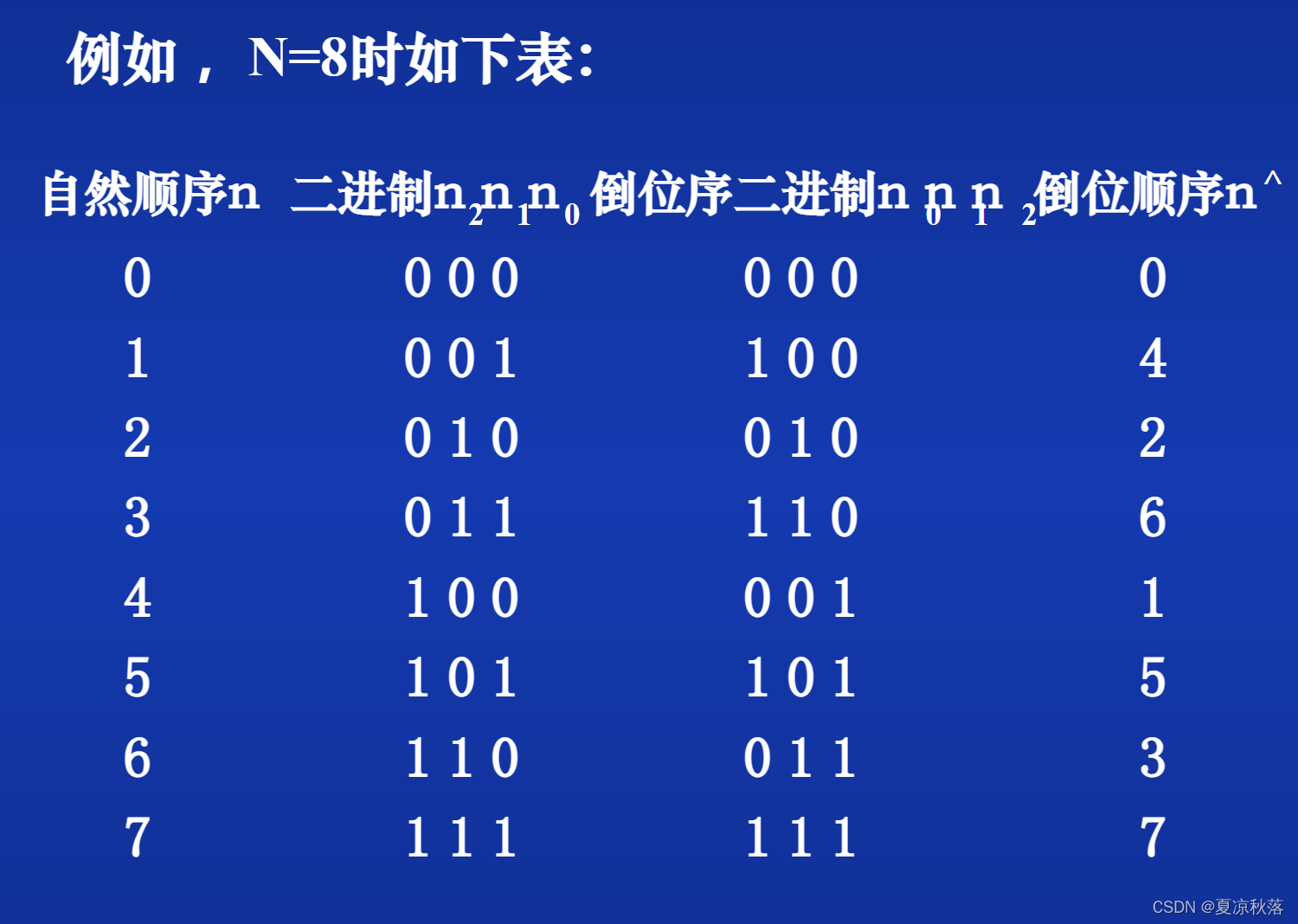

4、反傅里叶变化



5、 参考资料
【1】快速傅里叶变换FFT解析
【2】快速傅里叶变换(FFT)的推导过程(DIT)
【3】快速傅里叶变换FFTppt课件.ppt
【4】1024点fft原理及fpga实现
【5】快速傅里叶变换FFT-PPT(精







 本文详细介绍了离散傅里叶变换(DFT)的数学表达式及其计算复杂性,重点讲解了快速傅里叶变换(FFT)的基本思想、WNknW_N^{kn}
本文详细介绍了离散傅里叶变换(DFT)的数学表达式及其计算复杂性,重点讲解了快速傅里叶变换(FFT)的基本思想、WNknW_N^{kn}
















 1076
1076

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








