力扣每日一题70——爬楼梯

---

前言

爬楼梯是一道很经典的题目，本文提供两种方法。
题目：假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

---

一、示例

二、思路和代码

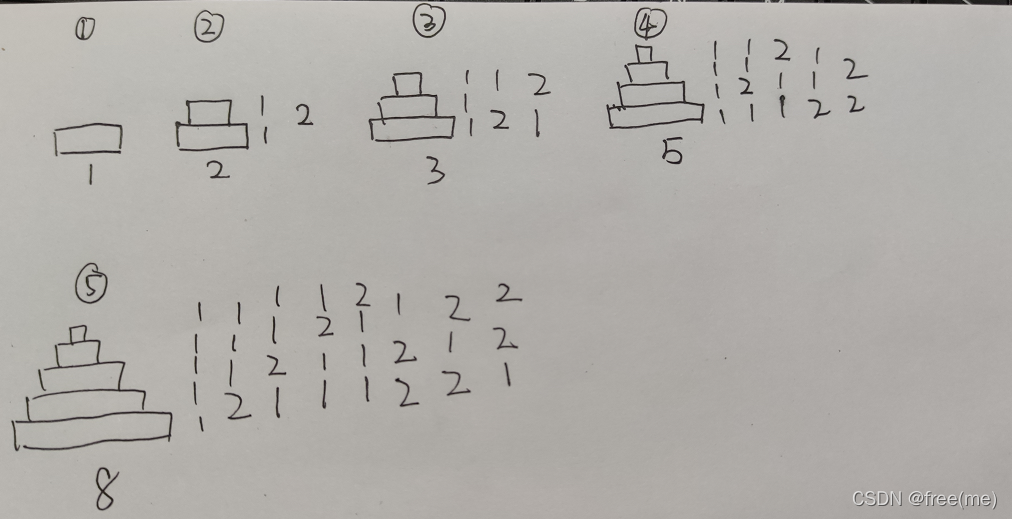
1.思路

如图所示：第三个是第一个和第二个相加，
第四个是第二个和第三个相加。

2.代码

#if 0
int func(int n) {
    int sum = 0;
    if(1 == n) {
        sum = 1;
    }
    if(2 == n) {
        sum = 2;
    }
    if(n > 2) {
        sum = func(n-1) + func(n-2);
    }
    return sum;

}

int climbStairs(int n){
    return func(n); //递归超时
}

#elif 1
int climbStairs(int n){
    int i;
    int* arr = (int*)malloc(sizeof(int) * 46);
    arr[0] = 1; arr[1] = 2;
    for(i = 2; i < 45; i++) {
        arr[i] = arr[i-1] + arr[i-2];
    }

    return arr[n-1];
}

#endif 

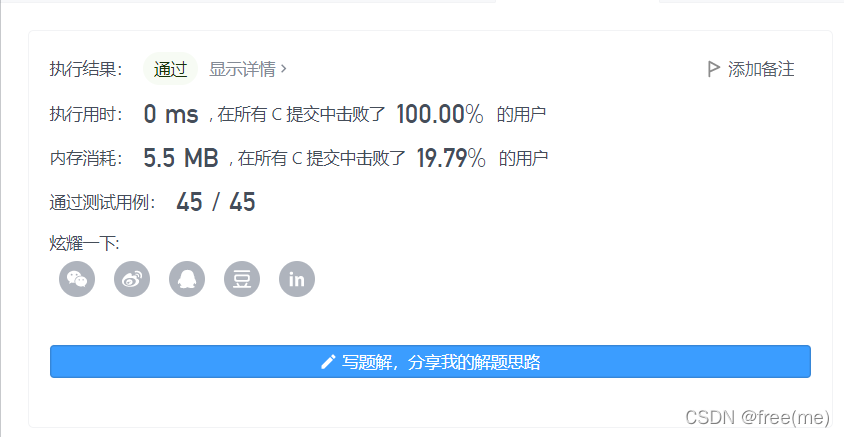
结果如图所示：

---